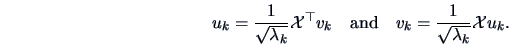The aim of this section is to present a duality relationship
between the two approaches shown in Sections 8.2 and 8.3.
Consider the eigenvector equations in 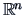
 |
(8.6) |
for 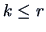 , where
, where
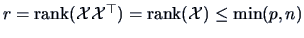 .
Multiplying by
.
Multiplying by
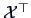 , we have
, we have
so that each eigenvector 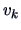 of
of
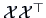 corresponds to an
eigenvector
corresponds to an
eigenvector
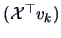 of
of
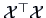 associated with the same eigenvalue
associated with the same eigenvalue 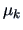 .
This means that every non-zero eigenvalue of
.
This means that every non-zero eigenvalue of
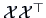 is an eigenvalue
of
is an eigenvalue
of
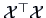 . The corresponding eigenvectors are related by
. The corresponding eigenvectors are related by
where 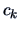 is some constant.
is some constant.
Now consider the eigenvector equations in 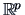 :
:
 |
(8.9) |
for 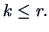 Multiplying by
Multiplying by  , we have
, we have
 |
(8.10) |
i.e., each eigenvector 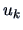 of
of
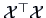 corresponds to an
eigenvector
corresponds to an
eigenvector 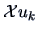 of
of
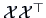 associated with the
same eigenvalue
associated with the
same eigenvalue 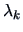 .
Therefore, every non-zero eigenvalue of
.
Therefore, every non-zero eigenvalue of
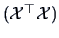 is an
eigenvalue of
is an
eigenvalue of
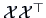 . The corresponding eigenvectors are related by
. The corresponding eigenvectors are related by
where 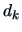 is some constant.
Now, since
is some constant.
Now, since
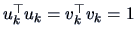 we have
we have
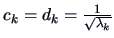 . This lead to the following result:
. This lead to the following result:
THEOREM 8.4 (Duality Relations
)
Let
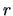
be the rank of

. For
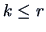
, the eigenvalues
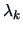
of
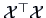
and
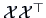
are the same
and the eigenvectors
(
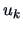
and
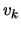
, respectively) are related by
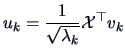 |
|
|
(8.11) |
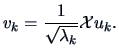 |
|
|
(8.12) |
Note that the projection of the  variables
on the factorial axis
variables
on the factorial axis  is given by
is given by
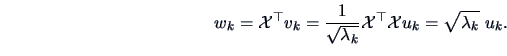 |
(8.13) |
Therefore, the eigenvectors 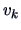 do not have to be explicitly
recomputed to get
do not have to be explicitly
recomputed to get 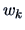 .
.
Note that 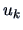 and
and 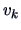 provide the SVD of
provide the SVD of  (see Theorem
2.2). Letting
(see Theorem
2.2). Letting
![$U=[u_1\; u_2\; \ldots \; u_r], \;
V=[v_1\; v_2\; \ldots \; v_r]$](mvahtmlimg2582.gif) and
and
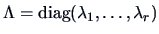 we have
we have
so that
 |
(8.14) |
In the following section
this method is applied in analysing consumption behavior
across different household types.
Summary

-
The matrices
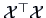 and
and
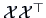 have the
same non-zero eigenvalues
have the
same non-zero eigenvalues
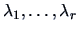 , where
, where
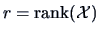 .
.

-
The eigenvectors of
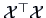 can be calculated from the
eigenvectors of
can be calculated from the
eigenvectors of
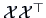 and vice versa:
and vice versa:

-
The coordinates representing the variables (columns) of
 in a
in a
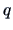 -dimensional subspace can be easily calculated by
-dimensional subspace can be easily calculated by
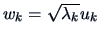 .
.
![]()
![]() :
:
![]() variables
on the factorial axis
variables
on the factorial axis ![]() is given by
is given by
![]() and
and ![]() provide the SVD of
provide the SVD of ![]() (see Theorem
2.2). Letting
(see Theorem
2.2). Letting ![]() and
and
![]() we have
we have