8.2 Fitting the $p$-dimensional Point Cloud

Subspaces of Dimension 1

In this section $\data{X}$ is represented by a cloud of $n$ points in $\mathbb{R}^p$ (considering each row). The question is how to project this point cloud onto a space of lower dimension. To begin consider the simplest problem, namely finding a subspace of dimension $1$. The problem boils down to finding a straight line $F_1$ through the origin. The direction of this line can be defined by a unit vector $u_1 \in \mathbb{R}^p$. Hence, we are searching for the vector $u_{1}$ which gives the ``best'' fit of the initial cloud of $n$ points. The situation is depicted in Figure 8.3.

Figure 8.3:

The representation of the $i$-th individual $x_i\in \mathbb{R}^p$ on this line is obtained by the projection of the corresponding point onto $u_1$, i.e., the projection point $p_{x_{i}}$. We know from (2.42) that the coordinate of $x_i$ on $F_1$ is given by

$$p_{x_i}=x^{\top}_i\frac{u_1} {\Vert u_1\Vert}=x^{\top}_iu_1 .$$ (8.1)

We define the best line $F_{1}$ in the following ``least-squares'' sense: Find $u_1 \in \mathbb{R}^p$ which minimizes

$$\sum^n_{i=1}\Vert x_i- p_{x_i}\Vert^2.$$ (8.2)

Since $\Vert x_i - p_{x_i}\Vert^2 = \Vert x_i\Vert^2 - \Vert p_{x_i}\Vert^2$ by Pythagoras's theorem, the problem of minimizing (8.2) is equivalent to maximizing $\sum_{i=1}^n \Vert p_{x_{i}}\Vert^2$. Thus the problem is to find $u_1 \in \mathbb{R}^p$ that maximizes $\sum^n_{i=1}\Vert p_{x_i}\Vert^2$ under the constraint $\Vert u_1\Vert=1$. With (8.1) we can write

$$\left( \begin{array}{c} p_{x_1} \\ p_{x_2} \\ \vdots \\ p_... ... \vdots \\ x^{\top}_nu_1 \end{array} \right) = \data{X}u_1 \$$

and the problem can finally be reformulated as: find $u_1 \in \mathbb{R}^p$ with $\Vert u_1\Vert=1$ that maximizes the quadratic form $(\data{X}u_1)^{\top}(\data{X}u_1)$ or

$$\max_{u^{\top}_1u_1=1} u^{\top}_1(\data{X}^{\top}\data{X})u_1.$$ (8.3)

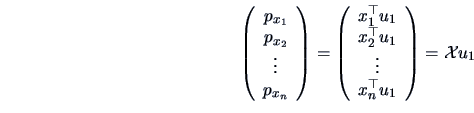
The solution is given by Theorem 2.5 (using $\data{A}=\data{X}^{\top}\data{X}$ and $\data{B}=\data{I}$ in the theorem).

THEOREM 8.1   The vector $u_1$ which minimizes (8.2) is the eigenvector of $\data{X}^{\top}\data{X}$ associated with the largest eigenvalue $\lambda_1$ of $\data{X}^{\top}\data{X}$.

Note that if the data have been centered, i.e., $\overline{x}=0$, then $\data{X}=\data{X}_c$, where $\data{X}_c$ is the centered data matrix, and $\frac{1}{n} \data{X}^{\top}\data{X}$ is the covariance matrix. Thus Theorem 8.1 says that we are searching for a maximum of the quadratic form (8.3) w.r.t. the covariance matrix $\data{S}_{\data{X}}=n^{-1}\data{X}^{\top}\data{X}$.

Representation of the Cloud on $F_1$

The coordinates of the $n$ individuals on $F_1$ are given by $\data{X}u_1$. $\data{X}u_1$ is called the first factorial variable or the first factor and $u_1$ the first factorial axis. The $n$ individuals, $x_{i}$, are now represented by a new factorial variable $z_{1}=\data{X}u_1$. This factorial variable is a linear combination of the original variables $(x_{\column{1}},\ldots,x_{\column{p}})$ whose coefficients are given by the vector $u_1$, i.e.,

$$z_{1}=u_{11}x_{\column{1}}+\ldots+u_{p1}x_{\column{p}}.$$ (8.4)

Subspaces of Dimension 2

If we approximate the $n$ individuals by a plane (dimension 2), it can be shown via Theorem 2.5 that this space contains $u_1$. The plane is determined by the best linear fit ($u_{1}$) and a unit vector $u_2$ orthogonal to $u_1$ which maximizes the quadratic form $u^{\top}_2(\data{X}^{\top}\data{X})u_2$ under the constraints

$$\Vert u_{2}\Vert=1,\ \textrm{and}\ u_{1}^{\top}u_{2}=0.$$

THEOREM 8.2   The second factorial axis, $u_2$, is the eigenvector of $\data{X}^{\top}\data{X}$ corresponding to the second largest eigenvalue $\lambda_2$ of $\data{X}^{\top}\data{X}$.

The unit vector $u_2$ characterizes a second line, $F_2$, on which the points are projected. The coordinates of the $n$ individuals on $F_2$ are given by $z_{2}=\data{X}u_2$. The variable $z_2$ is called the second factorial variable or the second factor. The representation of the $n$ individuals in two-dimensional space ( $z_{1}=\data{X} u_{1}$ vs. $z_{2}=\data{X} u_{2}$) is shown in Figure 8.4.

Figure 8.4: Representation of the individuals $x_{1},\ldots ,x_{n}$ as a two-dimensional point cloud.

Subspaces of Dimension $q\ (q\le p)$

In the case of $q$ dimensions the task is again to minimize (8.2) but with projection points in a $q$-dimensional subspace. Following the same argument as above, it can be shown via Theorem 2.5 that this best subspace is generated by $u_1,u_2,\ldots ,u_q$, the orthonormal eigenvectors of $\data{X}^{\top}\data{X}$ associated with the corresponding eigenvalues $\lambda _1\ge \lambda _2\ge \ldots \ge \lambda _q$. The coordinates of the $n$ individuals on the $k$-th factorial axis, $u_k$, are given by the $k$-th factorial variable $z_{k} = \data{X}u_k$ for $k=1, \ldots, q$. Each factorial variable $z_{k} = (z_{1k}, z_{2k}, \ldots, z_{nk})^{\top}$ is a linear combination of the original variables $x_{\column{1}}, x_{\column{2}}, \ldots, x_{\column{p}}$ whose coefficients are given by the elements of the $k$-th vector $u_k: z_{ik} = \sum_{m=1}^p x_{im} u_{mk}$.

Summary

$\ast$

The $p$-dimensional point cloud of individuals can be graphically represented by projecting each element into spaces of smaller dimensions.

$\ast$

The first factorial axis is $u_{1}$ and defines a line $F_{1}$ through the origin. This line is found by minimizing the orthogonal distances (8.2). The factor $u_{1}$ equals the eigenvector of $\data{X}^{\top}\data{X}$ corresponding to its largest eigenvalue. The coordinates for representing the point cloud on a straight line are given by $z_{1}=\data{X} u_{1}$.

$\ast$

The second factorial axis is $u_{2}$, where $u_{2}$ denotes the eigenvector of $\data{X}^{\top}\data{X}$ corresponding to its second largest eigenvalue. The coordinates for representing the point cloud on a plane are given by $z_{1}=\data{X} u_{1}$ and $z_{2}=\data{X} u_{2}$.

$\ast$

The factor directions $1, \ldots, q$ are $u_{1}, \ldots, u_{q}$, which denote the eigenvectors of $\data{X}^{\top}\data{X}$ corresponding to the $q$ largest eigenvalues. The coordinates for representing the point cloud of individuals on a $q$-dimensional subspace are given by $z_{1} = \data{X}u_{1}, \ldots, z_{q} = \data{X}u_{q}$.