In practice the PC transformation has to be replaced by the
respective estimators: 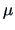 becomes
becomes 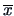 ,
, 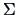 is replaced by
is replaced by 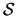 , etc.
If
, etc.
If 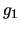 denotes the first eigenvector of
denotes the first eigenvector of 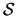 ,
the first principal component is given by
,
the first principal component is given by
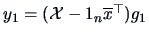 .
More generally if
.
More generally if
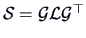 is the
spectral decomposition of
is the
spectral decomposition of 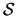 , then the PCs are
obtained by
, then the PCs are
obtained by
 |
(9.10) |
Note that with the centering matrix
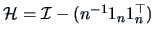 and
and
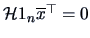 we can write
we can write
where
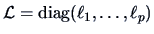 is the matrix of eigenvalues of
is the matrix of eigenvalues of 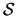 .
Hence the variance of
.
Hence the variance of 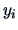 equals the eigenvalue
equals the eigenvalue 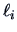 !
!
The PC technique is sensitive
to scale changes. If we multiply one variable by a scalar we
obtain different eigenvalues and eigenvectors. This is due to the fact that
an eigenvalue decomposition is performed on of the covariance matrix and not on
the correlation matrix (see Section 9.5).
The following warning is therefore important:
1mm
![\begin{picture}(2.00,2.00)
\par\linethickness{1.0pt}\put(0.00,0.00){\line(1,0){1...
...\line(1,-2){5.00}}
\put(5.00,4.00){\makebox(0,0)[cc]{\LARGE\bf !}}
\end{picture}](mvahtmlimg711.gif)
The PC transformation should be applied to data
that have approximately the same scale in each variable.
EXAMPLE 9.2
Let us apply this technique to the bank data set.
In this example we do not standardize the data.
Figure
9.3 shows some PC plots of the bank data set. The
genuine and counterfeit bank notes are marked by ``o'' and ``+'' respectively.
Recall that the mean vector of  is
is
The vector of eigenvalues of
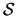
is
The eigenvectors
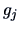
are given by the columns of the matrix
The first column of
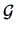
is the first eigenvector
and gives the weights used in the linear combination
of the original data in the first PC.
EXAMPLE 9.3
To see how sensitive the PCs are to a change in the scale of the variables,
assume that
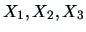
and
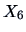
are measured in
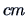
and that
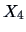
and
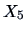
remain in
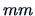
in the bank data set.
This leads to:
The covariance matrix can be obtained from
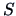
in (
3.4)
by dividing rows 1, 2, 3, 6 and columns 1, 2, 3, 6 by 10.
We obtain:
which clearly differs from Example
9.2.
Only the first two eigenvectors are given:
Comparing these results to the first two columns of
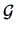
from Example
9.2, a completely different story is revealed.
Here the first component is dominated by
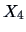
(lower margin)
and the second by
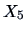
(upper margin),
while all of the other variables have much less weight.
The results are shown in Figure
9.4.
Section
9.5 will show how to select
a reasonable standardization of the
variables when the scales are too different.
Figure 9.4:
Principal components of the rescaled bank data.
 MVApcabankr.xpl
MVApcabankr.xpl
|
|
Summary

-
The scale of the variables should be roughly the same for PC transformations.

-
For the practical implementation of
principal components
analysis (PCA) we replace
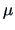 by
the mean
by
the mean 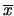 and
and 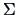 by the empirical covariance
by the empirical covariance 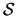 .
Then we compute the eigenvalues
.
Then we compute the eigenvalues
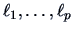 and the eigenvectors
and the eigenvectors
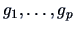 of
of
 .
The graphical representation of the PCs
is obtained by plotting the first PC vs. the second
(and eventually vs. the third).
.
The graphical representation of the PCs
is obtained by plotting the first PC vs. the second
(and eventually vs. the third).

-
The components of the eigenvectors
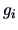 are the weights
of the original variables in the PCs.
are the weights
of the original variables in the PCs.
![]() becomes
becomes ![]() ,
, ![]() is replaced by
is replaced by ![]() , etc.
If
, etc.
If ![]() denotes the first eigenvector of
denotes the first eigenvector of ![]() ,
the first principal component is given by
,
the first principal component is given by
![]() .
More generally if
.
More generally if
![]() is the
spectral decomposition of
is the
spectral decomposition of ![]() , then the PCs are
obtained by
, then the PCs are
obtained by
![]()
![]() is
is
