EXAMPLE 9.8
Let us now apply the PCA to the
standardized bank data set
(Table
B.2).
Figure
9.13 shows some PC plots of the bank data set. The
genuine and counterfeit bank notes are marked by ``o'' and ``+'' respectively.
Figure 9.13:
Principal components of the standardized bank data.
 MVAnpcabank.xpl
MVAnpcabank.xpl
|
|
The vector of eigenvalues of 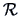 is
is
The eigenvectors
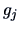
are given by the columns of the matrix
Each original variable has the same weight in the analysis and the results
are independent of the scale of each variable.
Figure 9.14:
The correlations of the original variable with the PCs.
 MVAnpcabanki.xpl
MVAnpcabanki.xpl
|
|
Table:
Eigenvalues and proportions of explained variance
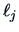 |
proportion of variances |
cumulated proportion |
| 2.946 |
0.491 |
49.1 |
| 1.278 |
0.213 |
70.4 |
| 0.869 |
0.145 |
84.9 |
| 0.450 |
0.075 |
92.4 |
| 0.264 |
0.045 |
96.9 |
| 0.189 |
0.032 |
100.0 |
|
Table:
Correlations with PCs
| |
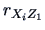 |
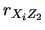 |
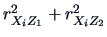 |
 : length : length |
 0.012 0.012 |
 0.922 0.922 |
0.85 |
 : left height : left height |
0.803 |
 0.387 0.387 |
0.79 |
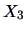 : right height : right height |
0.835 |
 0.285 0.285 |
0.78 |
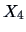 : lower : lower |
0.698 |
0.301 |
0.58 |
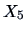 : upper : upper |
0.631 |
0.104 |
0.41 |
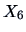 : diagonal : diagonal |
 0.847 0.847 |
 0.310 0.310 |
0.81 |
|
The proportions of explained variance are given in Table 9.7.
It can be concluded that the representation in two dimensions
should be sufficient. The
correlations leading to Figure 9.14 are given in Table 9.8.
The picture is different from the one obtained in Section 9.3
(see Table 9.2).
Here, the first factor is mainly a left-right vs. diagonal factor
and the second one
is a length factor (with negative weight).
Take another look at Figure 9.13, where the
individual bank notes are displayed. In the upper left graph
it can be seen that the genuine bank notes
are for the most part in the south-eastern portion of the graph featuring a
larger diagonal, smaller height (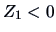 ) and also a
larger length (
) and also a
larger length (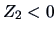 ). Note also that Figure 9.14
gives an idea of the correlation structure of the original data matrix.
). Note also that Figure 9.14
gives an idea of the correlation structure of the original data matrix.
EXAMPLE 9.9
Consider the data of 79 U.S. companies given in
Table
B.5. The data is first standardized by subtracting
the mean and dividing by the standard deviation.
Note that the data set contains six variables: assets
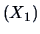
, sales
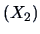
,
market value
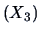
, profits
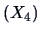
, cash flow
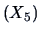
, number of employees
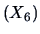
.
Calculating the corresponding vector of eigenvalues gives
and the matrix of eigenvectors is
Using this information the graphical representations of the first
two principal components are given in Figure
9.15.
The different sectors are marked by the following symbols:
| H |
... |
Hi Tech and Communication |
| E |
... |
Energy |
| F |
... |
Finance |
| M |
... |
Manufacturing |
| R |
... |
Retail |
 |
... |
all other sectors. |
Figure 9.15:
Principal components of the U.S. company data.
 MVAnpcausco.xpl
MVAnpcausco.xpl
|
|
Figure 9.16:
Principal components of the U.S. company data
(without IBM and General Electric).
 MVAnpcausco2.xpl
MVAnpcausco2.xpl
|
|
The two outliers in the
right-hand side of the graph are IBM and General Electric (GE), which
differ from the other companies with their
high market values.
As can be seen in the first column of  ,
market value has the largest weight
in the first PC, adding to the isolation of these two companies.
If IBM and GE were to be excluded from the data set, a completely
different picture would emerge, as shown in Figure 9.16.
In this case the vector of eigenvalues becomes
,
market value has the largest weight
in the first PC, adding to the isolation of these two companies.
If IBM and GE were to be excluded from the data set, a completely
different picture would emerge, as shown in Figure 9.16.
In this case the vector of eigenvalues becomes
and the corresponding matrix of eigenvectors is
Table:
Eigenvalues and proportions of explained variance.
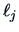 |
proportion of variance |
cumulated proportion |
| 3.191 |
0.532 |
0.532 |
| 1.535 |
0.256 |
0.788 |
| 0.791 |
0.132 |
0.920 |
| 0.292 |
0.049 |
0.968 |
| 0.149 |
0.025 |
0.993 |
| 0.041 |
0.007 |
1.000 |
|
The percentage of variation explained by each component
is given in Table
9.9.
The first two components explain almost 79% of the variance.
The interpretation of
the factors (the axes of Figure
9.16) is given in the table
of correlations (Table
9.10).
The first two columns of this table are plotted in Figure
9.17.
Table:
Correlations with PCs.
| |
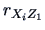 |
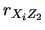 |
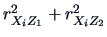 |
 : assets : assets |
0.47 |
 0.510 0.510 |
0.48 |
 : sales : sales |
0.78 |
 0.500 0.500 |
0.87 |
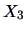 : market value : market value |
0.89 |
 0.003 0.003 |
0.80 |
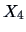 : profits : profits |
0.59 |
0.770 |
0.95 |
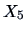 : cash flow : cash flow |
0.79 |
0.560 |
0.94 |
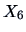 : employees : employees |
0.76 |
 0.340 0.340 |
0.70 |
|
Figure 9.17:
The correlation of the original variables with the PCs.
 MVAnpcausco2i.xpl
MVAnpcausco2i.xpl
|
|
From Figure 9.17 (and Table 9.10)
it appears that the first
factor is a ``size effect'', it is positively correlated with all the variables
describing the size of the activity of the companies. It is also a measure of the
economic strength of the firms. The second factor describes the ``shape'' of the
companies (``profit-cash flow'' vs. ``assets-sales'' factor), which is more
difficult to interpret from an economic point of view.
![]() is
is

![]() ) and also a
larger length (
) and also a
larger length (![]() ). Note also that Figure 9.14
gives an idea of the correlation structure of the original data matrix.
). Note also that Figure 9.14
gives an idea of the correlation structure of the original data matrix.
![\includegraphics[width=1\defpicwidth]{pcastd1a.ps}](mvahtmlimg2923.gif)
![\includegraphics[width=1\defpicwidth]{banki.ps}](mvahtmlimg2926.gif)

![\includegraphics[width=1\defpicwidth]{pcaus1neu.ps}](mvahtmlimg2932.gif)
![\includegraphics[width=1\defpicwidth]{pcaus2neu.ps}](mvahtmlimg2933.gif)

![\includegraphics[width=1\defpicwidth]{npcausco2i.ps}](mvahtmlimg2937.gif)
![\includegraphics[width=1\defpicwidth]{neuesbild1.ps}](mvahtmlimg2938.gif)
![\includegraphics[width=1\defpicwidth]{npcatime2.ps}](mvahtmlimg2939.gif)