Recall that the main idea of PC transformations is to find the most
informative projections
that maximize variances. The most informative SLC is given by the first
eigenvector.
In Section 9.2 the eigenvectors were calculated for the bank data.
In particular, with centered ![]() 's, we had:
's, we had:
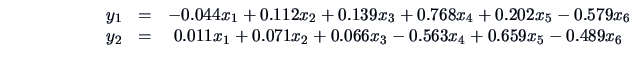
Hence, the first PC is essentially the difference between the bottom frame variable and the diagonal. The second PC is best described by the difference between the top frame variable and the sum of bottom frame and diagonal variables.
The weighting of the PCs tells us in which directions, expressed in
original coordinates, the best variance explanation is obtained.
A measure of how
well the first ![]() PCs explain variation is given by the relative proportion:
PCs explain variation is given by the relative proportion:
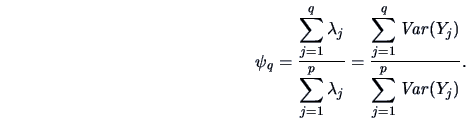 |
(9.12) |
|
Referring to the bank data example 9.2,
the (cumulative) proportions of explained
variance are given in Table 9.1.
The first PC ![]() already explains 67% of the variation.
The first three
already explains 67% of the variation.
The first three ![]() PCs explain 93% of the variation.
Once again it should be noted that PCs are not scale invariant, e.g.,
the PCs derived from the correlation matrix give different results
than the PCs derived from the covariance matrix (see Section 9.5).
PCs explain 93% of the variation.
Once again it should be noted that PCs are not scale invariant, e.g.,
the PCs derived from the correlation matrix give different results
than the PCs derived from the covariance matrix (see Section 9.5).
A good graphical representation of the ability of the PCs to explain the variation
in the data is given by the scree plot shown in the lower righthand
window of Figure 9.3.
The scree plot can be modified by using the relative proportions
on the ![]() -axis, as is shown in Figure 9.5 for the bank data set.
-axis, as is shown in Figure 9.5 for the bank data set.
The covariance between the PC vector ![]() and the original vector
and the original vector ![]() is calculated with the help of (9.4) as follows:
is calculated with the help of (9.4) as follows:
| (9.13) | |||
In the space of the first two PCs we plot these proportions,
i.e.,
![]() versus
versus
![]() .
Figure 9.6 shows this for the bank notes example.
This plot shows which of the original variables are most
strongly correlated with
PC
.
Figure 9.6 shows this for the bank notes example.
This plot shows which of the original variables are most
strongly correlated with
PC ![]() and
and ![]() .
.
From (9.16) it obviously follows that
![]() so that the points are always
inside the circle of radius
so that the points are always
inside the circle of radius ![]() .
In the bank notes example, the variables
.
In the bank notes example, the variables ![]() ,
, ![]() and
and ![]() correspond to correlations
near the periphery of the circle and are thus well explained by the first
two PCs.
Recall that we have interpreted the first PC as being essentially the
difference between
correspond to correlations
near the periphery of the circle and are thus well explained by the first
two PCs.
Recall that we have interpreted the first PC as being essentially the
difference between ![]() and
and ![]() . This is also reflected in Figure
9.6 since the points corresponding to these
variables lie on different sides of the vertical axis. An analogous
remark applies to the second PC. We had seen that the second PC is
well described by the difference between
. This is also reflected in Figure
9.6 since the points corresponding to these
variables lie on different sides of the vertical axis. An analogous
remark applies to the second PC. We had seen that the second PC is
well described by the difference between ![]() and the sum of
and the sum of ![]() and
and
![]() . Now we are able to see this result again from Figure 9.6
since the point corresponding to
. Now we are able to see this result again from Figure 9.6
since the point corresponding to ![]() lies above the horizontal axis
and the points corresponding to
lies above the horizontal axis
and the points corresponding to ![]() and
and ![]() lie below.
lie below.
|
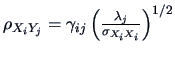 .
For a data matrix this translates into
.
For a data matrix this translates into
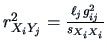 .
.