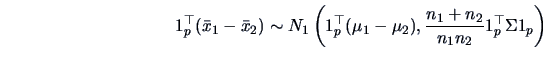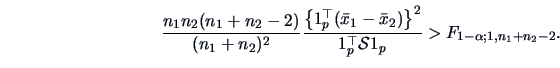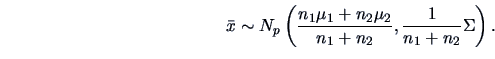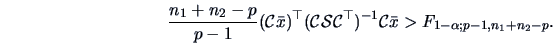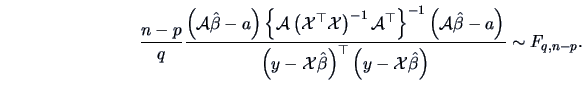In this section, we present a very general procedure which allows a
linear hypothesis to be tested, i.e.,
a linear restriction, either on a vector mean
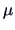 or on the coefficient
or on the coefficient 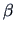 of a linear model.
The presented technique covers
many of the practical testing problems on means or regression coefficients.
of a linear model.
The presented technique covers
many of the practical testing problems on means or regression coefficients.
Linear hypotheses are of the form
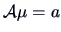 with known matrices
with known matrices
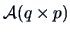 and
and 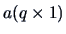 with
with 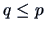 .
.
EXAMPLE 7.7
Let
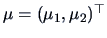
.
The hypothesis that
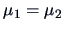
can be equivalently written as:
The general idea is to test a normal population
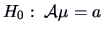 (restricted model) against the
full model
(restricted model) against the
full model 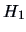 where no restrictions are put on
where no restrictions are put on 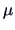 .
Due to the properties of the
multinormal, we can easily adapt the Test Problems 1 and 2 to this new
situation. Indeed we know, from Theorem 5.2, that
.
Due to the properties of the
multinormal, we can easily adapt the Test Problems 1 and 2 to this new
situation. Indeed we know, from Theorem 5.2, that
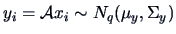 , where
, where
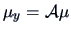 and
and
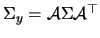 .
.
Testing the null
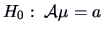 , is the same as testing
, is the same as testing
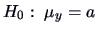 . The appropriate statistics are
. The appropriate statistics are 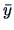 and
and 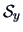 which
can be derived from the original statistics
which
can be derived from the original statistics 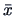 and
and 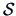 available
from
available
from 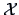 :
:
Here the difference between the sample mean and the tested value is
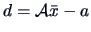 .
We are now in the situation to proceed to Test Problem 5 and 6.
.
We are now in the situation to proceed to Test Problem 5 and 6.
By (7.2) we have that, under 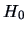 :
:
and we reject 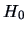 if this test statistic is too large at the desired
significance level.
if this test statistic is too large at the desired
significance level.
EXAMPLE 7.8
We consider hypotheses on partitioned mean vectors
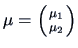
. Let us
first look at
for
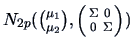
with known
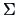
. This is
equivalent to
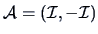
,
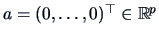
and leads to:
Another example is the test whether
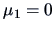
, i.e.,
for
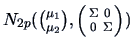
with known
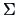
.
This is equivalent to
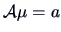
with
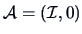
,
and
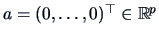
.
Hence:
From Corollary (5.4) and under 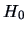 it follows immediately that
it follows immediately that
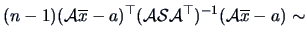 |
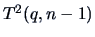 |
|
(7.9) |
since indeed under 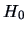 ,
,
is independent of
EXAMPLE 7.9
Let's come back again to the bank data set and suppose
that we want to test if
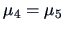
, i.e., the hypothesis that
the lower border mean equals the larger border mean for the forged bills.
In this case:
The test statistic is:
The observed value is
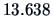
which is significant at the
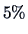
level.
In many situations, 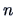 independent sampling units are observed at
independent sampling units are observed at 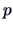 different times
or under
different times
or under 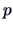 different experimental conditions (different treatments,...).
So here we repeat
different experimental conditions (different treatments,...).
So here we repeat 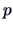 one-dimensional measurements on
one-dimensional measurements on 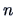 different
subjects. For instance, we observe the results from
different
subjects. For instance, we observe the results from 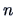 students
taking
students
taking 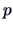 different exams. We end up with a
different exams. We end up with a 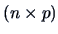 matrix.
We can thus consider the situation where
we have
matrix.
We can thus consider the situation where
we have
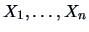 i.i.d. from a normal distribution
i.i.d. from a normal distribution
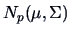 when there are
when there are 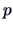 repeated measurements.
The hypothesis of interest in this case is that
there are no treatment effects,
repeated measurements.
The hypothesis of interest in this case is that
there are no treatment effects,
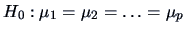 .
This hypothesis is a direct application of Test Problem 6.
Indeed, introducing an appropriate matrix transform on
.
This hypothesis is a direct application of Test Problem 6.
Indeed, introducing an appropriate matrix transform on 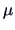 we have:
we have:
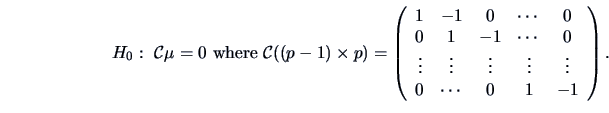 |
(7.10) |
Note that in many cases one of the experimental conditions is the ``control'' (a placebo,
standard drug or reference condition). Suppose it is the first component.
In that case one is interested in studying
differences to the control variable.
The matrix 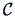 has therefore a different form
has therefore a different form
By (7.9) the null hypothesis will be rejected if:
As a matter of fact, 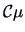 is the mean of the random
variable
is the mean of the random
variable
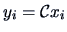
Simultaneous confidence intervals for linear combinations of the mean of 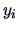 have been derived above in (7.7).
For all
have been derived above in (7.7).
For all
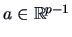 , with probability
, with probability 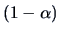 we have:
we have:
Due to the nature of the problem here, the row sums of the elements in
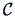 are zero:
are zero:
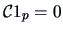 , therefore
, therefore
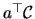 is a vector
whose sum of elements vanishes. This is called a
contrast. Let
is a vector
whose sum of elements vanishes. This is called a
contrast. Let
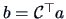 .
We have
.
We have
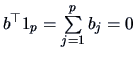 .
The result above thus provides for all contrasts of
.
The result above thus provides for all contrasts of
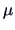 , and
, and 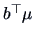 simultaneous confidence intervals at level
simultaneous confidence intervals at level 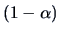
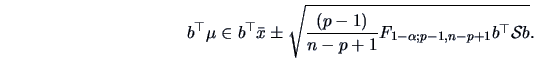
Examples of contrasts for 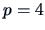 are
are
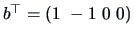 or
or 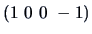 or even
or even
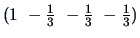 when the control is to be compared with the
mean of 3 different treatments.
when the control is to be compared with the
mean of 3 different treatments.
EXAMPLE 7.10
Bock (1975) considers the evolution of the vocabulary of children
from the eighth through eleventh grade.
The data set contains the scores of a vocabulary test of 40 randomly chosen
children that are observed from grades 8 to 11.
This is a repeated measurement situation,
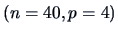
,
since the same children were observed from grades 8 to 11.
The statistics of interest are:
Suppose we are interested in the yearly evolution of the children.
Then the matrix
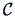
providing successive differences of
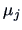
is:
The value of the test statistic is
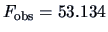
which is highly significant for
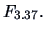
There are significant differences between the successive means.
However, the analysis of the contrasts shows the following simultaneous

confidence intervals
Thus, the rejection of
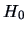
is mainly due to the difference between the
childrens' performances in the first and second year.
The confidence intervals for the following contrasts may also be of interest:
They show that
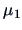
is different from the average of the 3 other years
(the same being true for
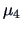
)
and
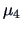
turns out to be higher than
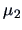
(and of course higher than
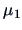
).
Test Problem 7 illustrates how the likelihood ratio
can be applied
when testing a linear restriction on
the coefficient 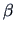 of a linear model.
It is also shown how a transformation of the test statistic leads to
an exact
of a linear model.
It is also shown how a transformation of the test statistic leads to
an exact 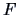 test as presented in Chapter 3.
test as presented in Chapter 3.
The constrained maximum likelihood estimators under 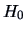 are
(Exercise 3.24):
are
(Exercise 3.24):
for 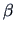 and
and
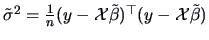 .
The estimate
.
The estimate 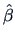 denotes the unconstrained MLE as before.
Hence, the LR statistic is
denotes the unconstrained MLE as before.
Hence, the LR statistic is
where 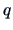 is the number of elements of
is the number of elements of 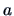 . This problem
also has an exact
. This problem
also has an exact 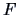 -test since
-test since
EXAMPLE 7.11
Let us continue with the ``classic blue'' pullovers. We can once more
test if
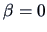
in the regression of sales on prices. It holds that
The LR statistic here is
which is not significant for the
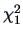
distribution. The
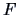
-test statistic
is also not significant. Hence, we can assume independence of
sales and prices (alone). Recall that this conclusion has to be revised if we
consider the prices together with advertisement costs and hours of
sales managers.
Recall the different conclusion that was made in Example 7.6
when we rejected
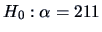 and
and 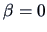 . The rejection there came from
the fact that the pair of values
was rejected. Indeed, if
. The rejection there came from
the fact that the pair of values
was rejected. Indeed, if 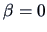 the estimator of
the estimator of 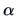 would be
would be
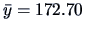 and this is too far from
and this is too far from 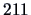 .
.
EXAMPLE 7.12
Let us now consider the multivariate regression in the ``classic blue''
pullovers example. From Example
3.15 we know that the
estimated parameters in the model
are
Hence, we could postulate the approximate relation:
which means in practice that augmenting the price by 20 EUR
requires the advertisement costs to increase by 10 EUR in order to keep
the number of pullovers sold constant. Vice versa, reducing the price by
20 EUR yields the same result as before if we reduced the advertisement
costs by 10 EUR. Let us now test whether the hypothesis
is valid. This is equivalent to
The LR statistic in this case is equal to (
 MVAlrtest.xpl
MVAlrtest.xpl
)
the
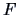
statistic is
Hence, in both cases we will not reject the null hypothesis.
In many situations, we want to compare two groups of individuals for whom a set
of 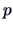 characteristics has been observed. We have two random samples
characteristics has been observed. We have two random samples
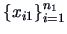 and
and
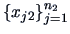 from two distinct
from two distinct
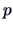 -variate normal populations. Several testing issues can be addressed in this
framework. In Test Problem 8
we will first test the hypothesis of equal mean
vectors in the two groups
under the assumption of equality of the two covariance
matrices. This task can be solved by adapting Test Problem 2.
-variate normal populations. Several testing issues can be addressed in this
framework. In Test Problem 8
we will first test the hypothesis of equal mean
vectors in the two groups
under the assumption of equality of the two covariance
matrices. This task can be solved by adapting Test Problem 2.
In Test Problem 9 a procedure for testing the equality of the
two covariance matrices is presented. If the covariance matrices differ,
the procedure of Test Problem 8 is no longer valid.
If the equality of the covariance matrices is rejected,
an easy rule for comparing two means with no
restrictions on the covariance matrices
is provided in Test Problem 10.
TEST PROBLEM 8
Assume that
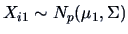 , with
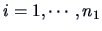 and
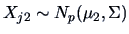 , with
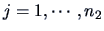 , where all the
variables are independent.
|
Both samples provide the statistics 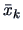 and
and 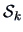 ,
, 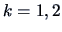 .
Let
.
Let
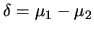 . We have
. We have
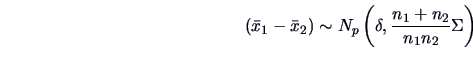 |
(7.11) |
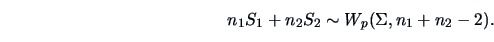 |
(7.12) |
Let 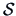 =
=
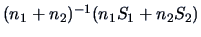 be the weighted
mean of
be the weighted
mean of 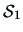 and
and 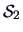 . Since the two samples are
independent and since
. Since the two samples are
independent and since 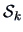 is independent of
is independent of 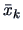 (for
(for 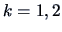 ) it follows that
) it follows that 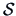 is independent of
is independent of
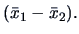 Hence, Theorem 5.8 applies
and leads to a
Hence, Theorem 5.8 applies
and leads to a 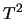 -distribution:
-distribution:
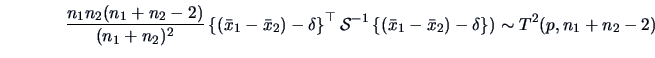 |
(7.13) |
or
This result, as in Test Problem 2, can be used to test
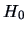 :
: 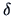 =0 or to construct a confidence region for
=0 or to construct a confidence region for
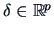 .
The rejection region is given by:
.
The rejection region is given by:
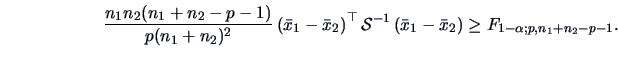 |
(7.14) |
A 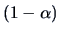 confidence region for
confidence region for 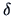 is given by the ellipsoid
centered at
is given by the ellipsoid
centered at
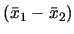
and the simultaneous confidence intervals for all linear combinations
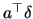 of the elements of
of the elements of 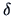 are given by
are given by
In particular we have at the 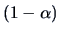 level, for
level, for 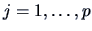 ,
,
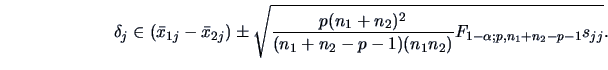 |
(7.15) |
EXAMPLE 7.13
Let us come back to the questions raised in Example
7.5.
We compare the means of assets (
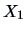
)
and of sales (
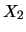
) for two sectors,
energy (group 1) and manufacturing (group 2).
With
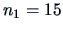
,
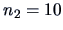
, and
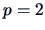
we obtain the statistics:
and
so that
The observed value of the test statistic (
7.14) is
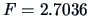
.
Since
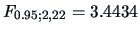
the hypothesis of equal means of the two groups is
not rejected although it would be rejected at a less severe level
(
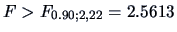
).
The 95% simultaneous confidence intervals for the differences
(
 MVAsimcidif.xpl
MVAsimcidif.xpl
) are given by
EXAMPLE 7.14
In order to illustrate the presented test procedures it is interesting to
analyze some simulated data.
This simulation will point out the importantce of the covariances in
testing means.
We created 2 independent normal
samples in
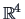
of sizes
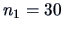
and
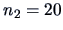
with:
One may consider this as an example of
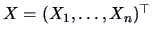
being the students' scores from 4 tests, where the 2 groups
of students were subjected to two different methods of teaching.
First we simulate the two samples with
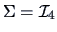
and
obtain the statistics:
The test statistic (
7.14) takes the value
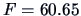
which
is highly significant: the small variance allows the difference
to be detected even
with these relatively moderate sample sizes.
We conclude (at the 95% level) that:
which confirms that the means for
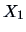
and
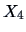
are different.
Consider now a different simulation scenario where the standard deviations are 4
times larger:
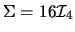 .
Here we obtain:
.
Here we obtain:
Now the test statistic takes the value 1.54 which is no longer significant
(
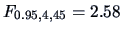
).
Now we cannot reject the null hypothesis (which we know to be false!) since
the increase in variances prohibits the detection of differences
of such magnitude.
The following situation illustrates once more the role of the covariances
between covariates.
Suppose that
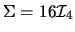 as above but with
as above but with
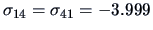 (this corresponds to a negative correlation
(this corresponds to a negative correlation
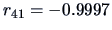 ).
We have:
).
We have:
The value of
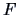
is
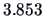
which is significant at the 5% level
(p-value = 0.0089). So the null hypothesis
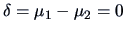
is outside
the 95% confidence ellipsoid. However, the simultaneous confidence intervals, which
do not take the covariances into account
are given by:
They contain the null value (see Remark
7.1 above) although they are very
asymmetric for
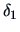
and
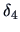
.
EXAMPLE 7.15
Let us compare the vectors of means of the forged and the genuine bank notes.
The matrices
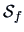
and
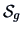
were given in Example
3.1 and since here
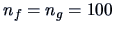
,
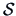
is the simple average of
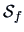
and
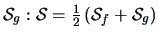
.
The test statistic is given by (
7.14) and turns out to be
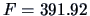
which is
highly significant for
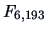
. The 95% simultaneous confidence intervals for the
differences
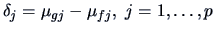
are:
All of the components (except for the first one)
show significant differences in the means. The main
effects are taken by the lower border
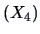
and the diagonal
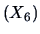
.
The preceding test implicitly uses the fact that the two samples are
extracted from two different populations with common variance 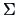 .
In this case, the test statistic (7.14) measures the distance between
the two centers of gravity of the two groups w.r.t. the common metric given by
the pooled variance matrix
.
In this case, the test statistic (7.14) measures the distance between
the two centers of gravity of the two groups w.r.t. the common metric given by
the pooled variance matrix 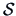 . If
. If
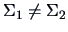 no such matrix exists.
There are no satisfactory test procedures for testing the equality of variance matrices
which are robust with respect to normality assumptions of the populations.
The following test extends Bartlett's test for equality of variances in the
univariate case. But this test is known to be very sensitive to
departures from normality.
no such matrix exists.
There are no satisfactory test procedures for testing the equality of variance matrices
which are robust with respect to normality assumptions of the populations.
The following test extends Bartlett's test for equality of variances in the
univariate case. But this test is known to be very sensitive to
departures from normality.
TEST PROBLEM 9
(Comparison of Covariance Matrices)
Let
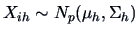 ,
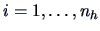 , 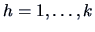
be independent random variables,
|
Each subsample provides 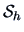 , an estimator of
, an estimator of 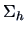 , with
, with
Under 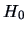 ,
,
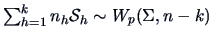 (Section 5.2), where
(Section 5.2), where
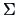 is the common covariance matrix
is the common covariance matrix 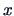 and
and
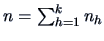 .
Let
.
Let
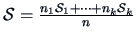 be the weighted
average of the
be the weighted
average of the 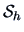 (this is in fact the MLE of
(this is in fact the MLE of 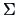 when
when 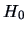 is true). The likelihood ratio test leads to the statistic
is true). The likelihood ratio test leads to the statistic
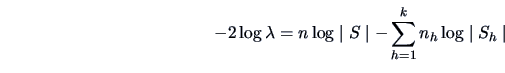 |
(7.16) |
which under 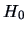 is approximately distributed as a
is approximately distributed as a
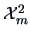 where
where
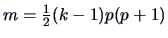 .
.
EXAMPLE 7.16
Let's come back to Example
7.13,
where the mean of assets and sales have been compared
for companies from the energy and manufacturing sector
assuming that
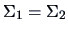
. The test of
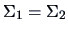
leads to the value of the test statistic
 |
(7.17) |
which is not significant (p-value for a
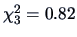
). We cannot reject
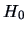
and the
comparison of the means performed above is valid.
EXAMPLE 7.17
Let us compare the covariance matrices of the
forged and the genuine bank notes (the matrices
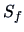
and
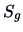
are shown in Example
3.1).
A first look seems to suggest that
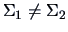
.
The pooled variance
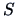
is given by
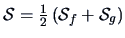
since here
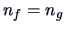
.
The test statistic here is
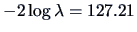
,
which is highly significant
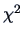
with 21 degrees of freedom. As expected,
we reject the hypothesis of equal covariance matrices,
and as a result the procedure for comparing the two means
in Example
7.15 is not valid.
What can we do with unequal covariance matrices? When both 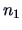 and
and 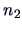 are large, we
have a simple solution:
are large, we
have a simple solution:
TEST PROBLEM 10
(Comparison of two means, unequal covariance matrices, large samples)
Assume that
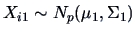 , with
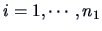 and
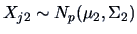 , with
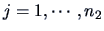 are independent random variables.
|
Letting
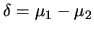 , we have
, we have
Therefore, by (5.4)
Since 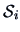 is a consistent estimator of
is a consistent estimator of 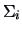 for
for 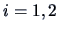 , we have
, we have
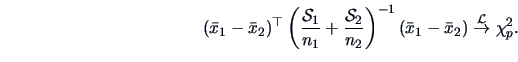 |
(7.18) |
This can be used in place of (7.13) for testing 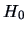 , defining a confidence
region for
, defining a confidence
region for 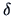 or constructing simultaneous confidence intervals for
or constructing simultaneous confidence intervals for
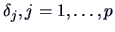 .
.
For instance, the rejection region at the level 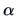 will be
will be
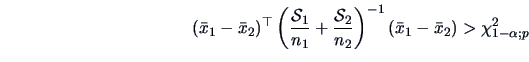 |
(7.19) |
and the 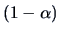 simultaneous confidence intervals for
simultaneous confidence intervals for 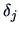 ,
,
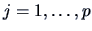 are:
are:
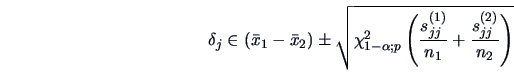 |
(7.20) |
where 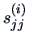 is the
is the 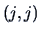 element of the matrix
element of the matrix 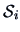 .
This may be compared to (7.15) where the pooled variance was used.
.
This may be compared to (7.15) where the pooled variance was used.
REMARK 7.2
We see, by comparing the statistics (
7.19) with (
7.14),
that we measure here
the distance between
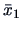
and
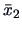
using the metric
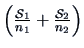
. It should be noticed that when
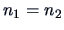
, the two methods are
essentially the same since then
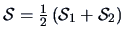
.
If the covariances are different but have the same eigenvectors
(different eigenvalues),
one can apply the common principal component (CPC) technique,
see Chapter
9.
EXAMPLE 7.18
Let us use the last test to compare the forged and the genuine bank notes again (
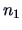
and
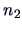
are both large). The test statistic (
7.19) turns out to be 2436.8 which is again
highly significant. The 95% simultaneous confidence intervals are:
showing that all the components except the first are different from zero, the larger difference
coming from
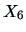
(length of the diagonal) and
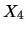
(lower border). The results are very
similar to those obtained in Example (
7.15). This is due to the fact that here
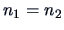
as we already mentioned in the remark above.
Profile Analysis
Another useful application of Test Problem 6
is the repeated measurements problem applied to two independent groups.
This problem arises in practice when
we observe repeated measurements of characteristics (or measures of the same type under different
experimental conditions) on the different groups which have to be compared.
It is important that the 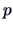 measures (the ``profile'') are comparable and
in particular are reported in the same units.
For instance, they may be measures of blood pressure at
measures (the ``profile'') are comparable and
in particular are reported in the same units.
For instance, they may be measures of blood pressure at 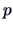 different
points in time, one group being the
control group and the other the group receiving a new treatment.
The observations may be the
scores obtained from
different
points in time, one group being the
control group and the other the group receiving a new treatment.
The observations may be the
scores obtained from 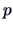 different tests of two different experimental groups.
One is then interested in comparing the profiles of each group:
the profile being just the vectors
of the means of the
different tests of two different experimental groups.
One is then interested in comparing the profiles of each group:
the profile being just the vectors
of the means of the 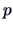 responses (the comparison may be visualized in a two dimensional graph
using the parallel coordinate plot introduced in Section 1.7).
responses (the comparison may be visualized in a two dimensional graph
using the parallel coordinate plot introduced in Section 1.7).
We are thus in the same statistical situation
as for the comparison of two means:
where all variables are independent.
Suppose the two population profiles look like Figure 7.1.
The following questions are of interest:
- Are the profiles similar in the sense of being parallel (which means no interaction
between the treatments and the groups)?
- If the profiles are parallel, are they at the same level?
- If the profiles are parallel, is there any treatment effect, i.e.,
are the profiles horizontal?
The above questions are easily translated into
linear constraints on the means and a test statistic can be obtained
accordingly.
Parallel Profiles
Let 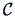 be a
be a 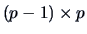 matrix defined as
matrix defined as
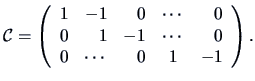
The hypothesis to be tested is
From (7.11), (7.12) and Corollary 5.4
we know that under 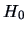 :
:
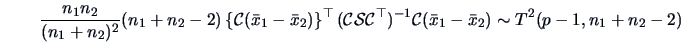 |
(7.21) |
where 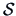 is the pooled covariance matrix.
The hypothesis is rejected if
is the pooled covariance matrix.
The hypothesis is rejected if
The question of equality of the two levels is meaningful only if the two profiles are parallel.
In the case of interactions (rejection of 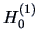 ), the two populations react differently to the
treatments and the question of the level has no meaning.
), the two populations react differently to the
treatments and the question of the level has no meaning.
The equality of the two levels can be formalized as
since
and
Using Corollary 5.4 we have that:
The rejection region is
If it is rejected that the profiles are parallel, then two independent
analyses should be
done on the two groups using the repeated measurement approach.
But if it is accepted that they are parallel,
then we can exploit the information
contained in both groups (eventually at different levels)
to test a treatment effect, i.e., if the two profiles are horizontal.
This may be written as:
Consider the average profile 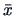 :
:
Clearly,
Now it is not hard to prove that 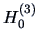 with
with 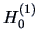 implies that
implies that
So under parallel, horizontal profiles we have
From Corollary 5.4 we again obtain
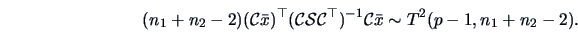 |
(7.23) |
This leads to the rejection region of 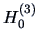 , namely
, namely
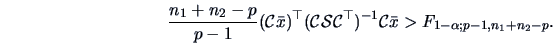
EXAMPLE 7.19
Morrison (1990) proposed a test in which the results of
4 sub-tests of the Wechsler Adult Intelligence Scale
(WAIS) are compared for 2 categories of people:
group 1 contains
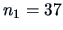
people who do not have a senile factor and
group 2 contains
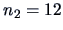
people who have a senile factor.
The four WAIS sub-tests are
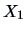
(information),
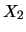
(similarities),
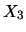
(arithmetic) and
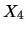
(picture completion).
The relevant statistics are
The test statistic for testing if the two profiles are parallel is
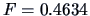
, which is not significant (
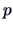
-value
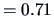
).
Thus it is accepted that the two are parallel.
The second test statistic
(testing the equality of the levels of the 2 profiles)
is
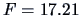
, which is highly
significant (
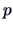
-value
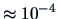
).
The global level of the test for the non-senile
people is superior to the senile group.
The final test (testing the horizontality of the average
profile) has the test statistic
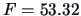
,
which is also highly significant (
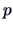
-value
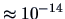
).
This implies that there are substantial differences among the means of the
different subtests.
Summary

-
Hypotheses about
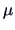 can often be written as
can often be written as 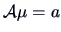 , with
matrix
, with
matrix 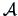 , and vector
, and vector 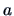 .
.

-
The hypothesis
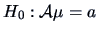 for
for
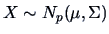 with
with 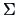 known leads to
known leads to
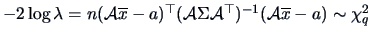 , where
, where 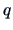 is the number of elements in
is the number of elements in 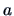 .
.

-
The hypothesis
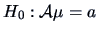 for
for
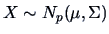 with
with 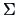 unknown leads to
unknown leads to
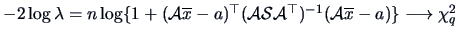 , where
, where 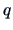 is the number of elements in
is the number of elements in 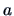 and we have an exact test
and we have an exact test
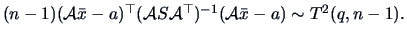

-
The hypothesis
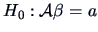 for
for
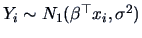 with
with 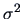 unknown leads to
unknown leads to
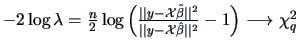 , with
, with 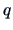 being the length of
being the length of 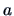 and with
and with
![]() or on the coefficient
or on the coefficient ![]() of a linear model.
The presented technique covers
many of the practical testing problems on means or regression coefficients.
of a linear model.
The presented technique covers
many of the practical testing problems on means or regression coefficients.
![]() with known matrices
with known matrices
![]() and
and ![]() with
with ![]() .
.
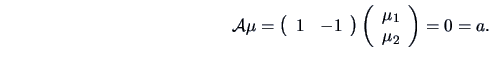
![]() (restricted model) against the
full model
(restricted model) against the
full model ![]() where no restrictions are put on
where no restrictions are put on ![]() .
Due to the properties of the
multinormal, we can easily adapt the Test Problems 1 and 2 to this new
situation. Indeed we know, from Theorem 5.2, that
.
Due to the properties of the
multinormal, we can easily adapt the Test Problems 1 and 2 to this new
situation. Indeed we know, from Theorem 5.2, that
![]() , where
, where
![]() and
and
![]() .
.
![]() , is the same as testing
, is the same as testing
![]() . The appropriate statistics are
. The appropriate statistics are ![]() and
and ![]() which
can be derived from the original statistics
which
can be derived from the original statistics ![]() and
and ![]() available
from
available
from ![]() :
:
![]() :
:
![]() it follows immediately that
it follows immediately that

![]() independent sampling units are observed at
independent sampling units are observed at ![]() different times
or under
different times
or under ![]() different experimental conditions (different treatments,...).
So here we repeat
different experimental conditions (different treatments,...).
So here we repeat ![]() one-dimensional measurements on
one-dimensional measurements on ![]() different
subjects. For instance, we observe the results from
different
subjects. For instance, we observe the results from ![]() students
taking
students
taking ![]() different exams. We end up with a
different exams. We end up with a ![]() matrix.
We can thus consider the situation where
we have
matrix.
We can thus consider the situation where
we have
![]() i.i.d. from a normal distribution
i.i.d. from a normal distribution
![]() when there are
when there are ![]() repeated measurements.
The hypothesis of interest in this case is that
there are no treatment effects,
repeated measurements.
The hypothesis of interest in this case is that
there are no treatment effects,
![]() .
This hypothesis is a direct application of Test Problem 6.
Indeed, introducing an appropriate matrix transform on
.
This hypothesis is a direct application of Test Problem 6.
Indeed, introducing an appropriate matrix transform on ![]() we have:
we have:
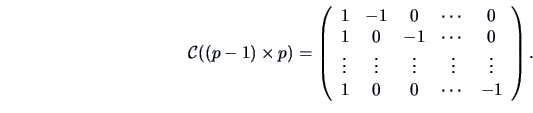
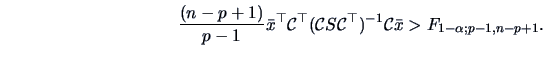
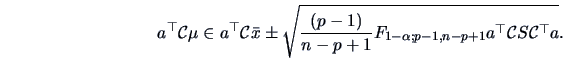
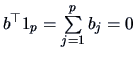 .
The result above thus provides for all contrasts of
.
The result above thus provides for all contrasts of
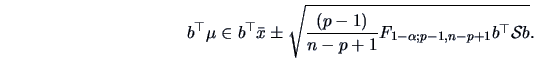
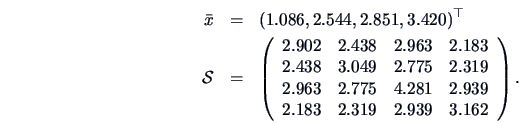
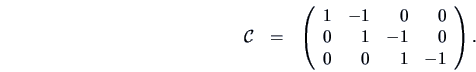

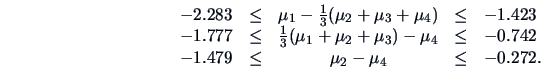
![]() of a linear model.
It is also shown how a transformation of the test statistic leads to
an exact
of a linear model.
It is also shown how a transformation of the test statistic leads to
an exact ![]() test as presented in Chapter 3.
test as presented in Chapter 3.
![]() are
(Exercise 3.24):
are
(Exercise 3.24):
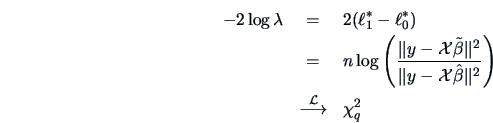
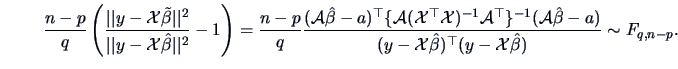



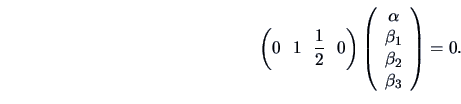
![]() characteristics has been observed. We have two random samples
characteristics has been observed. We have two random samples
![]() and
and
![]() from two distinct
from two distinct
![]() -variate normal populations. Several testing issues can be addressed in this
framework. In Test Problem 8
we will first test the hypothesis of equal mean
vectors in the two groups
under the assumption of equality of the two covariance
matrices. This task can be solved by adapting Test Problem 2.
-variate normal populations. Several testing issues can be addressed in this
framework. In Test Problem 8
we will first test the hypothesis of equal mean
vectors in the two groups
under the assumption of equality of the two covariance
matrices. This task can be solved by adapting Test Problem 2.
![]() and
and ![]() ,
, ![]() .
Let
.
Let
![]() . We have
. We have
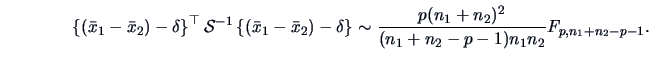
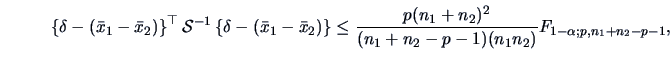
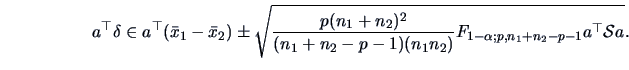
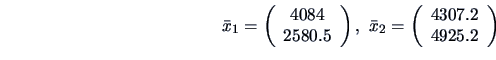
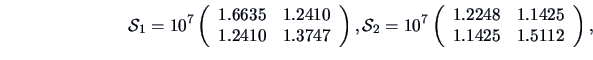
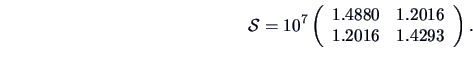


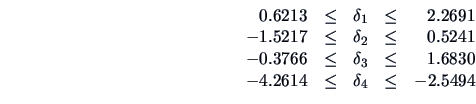
![]() .
Here we obtain:
.
Here we obtain:

![]() as above but with
as above but with
![]() (this corresponds to a negative correlation
(this corresponds to a negative correlation
![]() ).
We have:
).
We have:

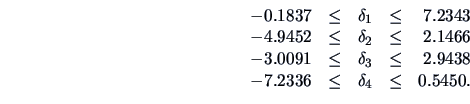
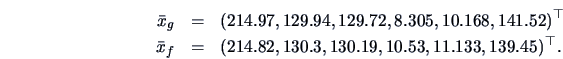
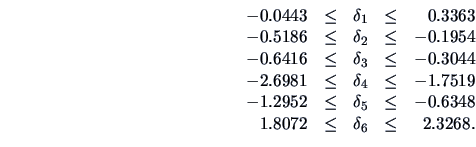
![]() .
In this case, the test statistic (7.14) measures the distance between
the two centers of gravity of the two groups w.r.t. the common metric given by
the pooled variance matrix
.
In this case, the test statistic (7.14) measures the distance between
the two centers of gravity of the two groups w.r.t. the common metric given by
the pooled variance matrix ![]() . If
. If
![]() no such matrix exists.
There are no satisfactory test procedures for testing the equality of variance matrices
which are robust with respect to normality assumptions of the populations.
The following test extends Bartlett's test for equality of variances in the
univariate case. But this test is known to be very sensitive to
departures from normality.
no such matrix exists.
There are no satisfactory test procedures for testing the equality of variance matrices
which are robust with respect to normality assumptions of the populations.
The following test extends Bartlett's test for equality of variances in the
univariate case. But this test is known to be very sensitive to
departures from normality.
![]() , an estimator of
, an estimator of ![]() , with
, with
![]() , we have
, we have
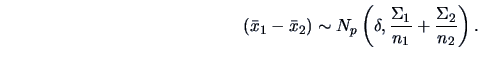
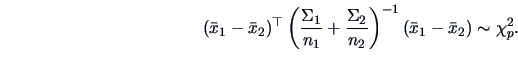
![]() will be
will be
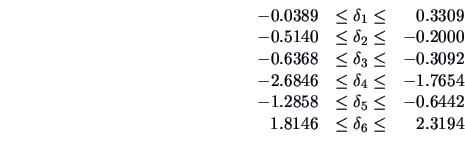
![]() measures (the ``profile'') are comparable and
in particular are reported in the same units.
For instance, they may be measures of blood pressure at
measures (the ``profile'') are comparable and
in particular are reported in the same units.
For instance, they may be measures of blood pressure at ![]() different
points in time, one group being the
control group and the other the group receiving a new treatment.
The observations may be the
scores obtained from
different
points in time, one group being the
control group and the other the group receiving a new treatment.
The observations may be the
scores obtained from ![]() different tests of two different experimental groups.
One is then interested in comparing the profiles of each group:
the profile being just the vectors
of the means of the
different tests of two different experimental groups.
One is then interested in comparing the profiles of each group:
the profile being just the vectors
of the means of the ![]() responses (the comparison may be visualized in a two dimensional graph
using the parallel coordinate plot introduced in Section 1.7).
responses (the comparison may be visualized in a two dimensional graph
using the parallel coordinate plot introduced in Section 1.7).
![]() be a
be a ![]() matrix defined as
matrix defined as
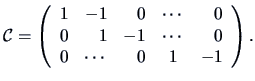
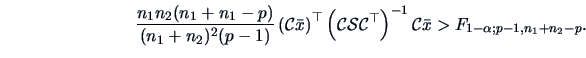
![]() ), the two populations react differently to the
treatments and the question of the level has no meaning.
), the two populations react differently to the
treatments and the question of the level has no meaning.