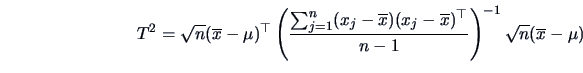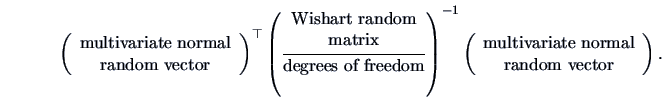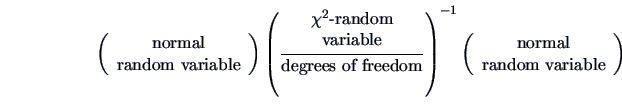Suppose that
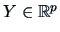 is a standard normal random vector, i.e.,
is a standard normal random vector, i.e.,
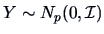 , independent of the random matrix
, independent of the random matrix
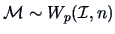 .
What is the distribution of
.
What is the distribution of
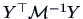 ? The answer is
provided by the Hotelling
? The answer is
provided by the Hotelling 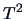 -distribution:
-distribution:
 is Hotelling
is Hotelling 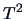
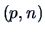 distributed.
distributed.
The Hotelling 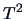 -distribution
is a generalization of the Student
-distribution
is a generalization of the Student 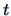 -distribution.
The general multinormal distribution
-distribution.
The general multinormal distribution 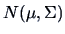 is considered
in Theorem 5.8. The Hotelling
is considered
in Theorem 5.8. The Hotelling 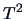 -distribution will play
a central role in hypothesis testing in Chapter 7.
-distribution will play
a central role in hypothesis testing in Chapter 7.
COROLLARY 5.3
If
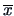
is the mean
of a sample drawn from a normal population
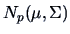
and
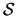
is the sample covariance matrix, then
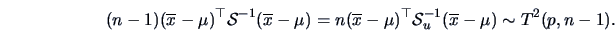 |
(5.17) |
Recall that
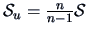 is an unbiased
estimator of the covariance matrix.
A connection between the Hotelling
is an unbiased
estimator of the covariance matrix.
A connection between the Hotelling 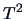 - and the
- and the 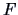 -distribution
is given by the next theorem.
-distribution
is given by the next theorem.
EXAMPLE 5.5
In the univariate case (p=1), this theorem boils down to the well
known result:
For further details on Hotelling 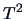 -distribution see
Mardia et al. (1979).
The next corollary follows immediately from (3.23),(3.24)
and from Theorem 5.8. It will be useful for testing linear restrictions
in multinormal populations.
-distribution see
Mardia et al. (1979).
The next corollary follows immediately from (3.23),(3.24)
and from Theorem 5.8. It will be useful for testing linear restrictions
in multinormal populations.
COROLLARY 5.4
Consider a linear transform of
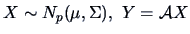
where
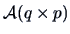
with
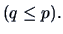
If
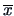
and
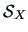
are the sample mean
and the covariance matrix, we have
The 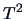 distribution is closely connected to the univariate
distribution is closely connected to the univariate 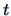 -statistic.
In Example 5.4 we described the manner in which the Wishart
distribution generalizes the
-statistic.
In Example 5.4 we described the manner in which the Wishart
distribution generalizes the 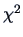 -distribution.
We can write (5.17) as:
-distribution.
We can write (5.17) as:
which is of the form
This is analogous to
or
for the univariate case. Since the multivariate normal and Wishart random
variables are independently distributed, their joint distribution is the
product of the marginal normal and Wishart distributions. Using calculus, the
distribution of 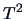 as given above can be derived from
this joint distribution.
as given above can be derived from
this joint distribution.
Summary

-
Hotelling's
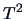 -distribution is a generalization of the
-distribution is a generalization of the
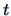 -distribution. In particular
-distribution. In particular
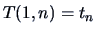 .
.

-
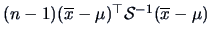 has a
has a 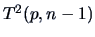 distribution.
distribution.

-
The relation between Hotelling's
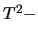 and Fisher's
and Fisher's 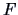 -distribution is given by
-distribution is given by
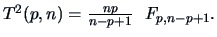
![]() is a standard normal random vector, i.e.,
is a standard normal random vector, i.e.,
![]() , independent of the random matrix
, independent of the random matrix
![]() .
What is the distribution of
.
What is the distribution of
![]() ? The answer is
provided by the Hotelling
? The answer is
provided by the Hotelling ![]() -distribution:
-distribution:
![]() is Hotelling
is Hotelling ![]()
![]() distributed.
distributed.
![]() -distribution
is a generalization of the Student
-distribution
is a generalization of the Student ![]() -distribution.
The general multinormal distribution
-distribution.
The general multinormal distribution ![]() is considered
in Theorem 5.8. The Hotelling
is considered
in Theorem 5.8. The Hotelling ![]() -distribution will play
a central role in hypothesis testing in Chapter 7.
-distribution will play
a central role in hypothesis testing in Chapter 7.
![]() is an unbiased
estimator of the covariance matrix.
A connection between the Hotelling
is an unbiased
estimator of the covariance matrix.
A connection between the Hotelling ![]() - and the
- and the ![]() -distribution
is given by the next theorem.
-distribution
is given by the next theorem.
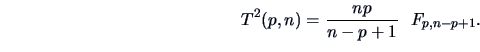
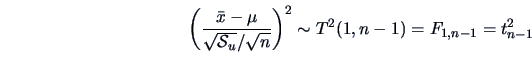
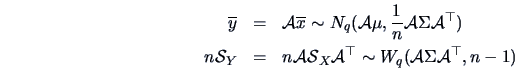
![]() distribution is closely connected to the univariate
distribution is closely connected to the univariate ![]() -statistic.
In Example 5.4 we described the manner in which the Wishart
distribution generalizes the
-statistic.
In Example 5.4 we described the manner in which the Wishart
distribution generalizes the ![]() -distribution.
We can write (5.17) as:
-distribution.
We can write (5.17) as: