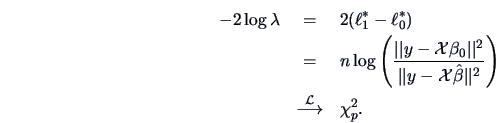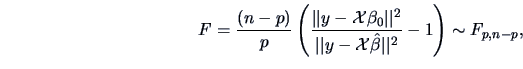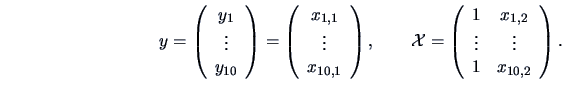7.1 Likelihood Ratio Test
Suppose that the distribution of
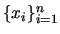 ,
,
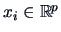 ,
depends on a parameter vector
,
depends on a parameter vector  .
We will consider two hypotheses:
.
We will consider two hypotheses:
The hypothesis 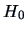 corresponds to the ``reduced model'' and
corresponds to the ``reduced model'' and 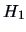 to the
``full model''. This notation was already used in Chapter 3.
to the
``full model''. This notation was already used in Chapter 3.
EXAMPLE 7.1
Consider a multinormal
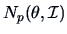
. To test if

equals a
certain fixed value
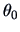
we construct the test problem:
or, equivalently,
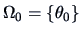
,
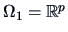
.
Define
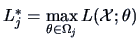 ,
the maxima of the likelihood for each of the hypotheses.
Consider the likelihood ratio (LR)
,
the maxima of the likelihood for each of the hypotheses.
Consider the likelihood ratio (LR)
 |
(7.1) |
One tends to favor 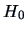 if the LR is high and
if the LR is high and 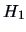 if the LR is low.
The likelihood ratio test (LRT) tells us when exactly
to favor
if the LR is low.
The likelihood ratio test (LRT) tells us when exactly
to favor 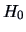 over
over 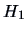 .
A likelihood ratio test of size
.
A likelihood ratio test of size 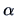 for testing
for testing 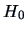 against
against
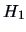 has the rejection region
has the rejection region
where 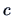 is determined so that
is determined so that
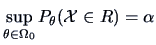 . The difficulty here is to express
. The difficulty here is to express  as a
function of
as a
function of 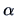 , because
, because
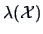 might be
a complicated function of
might be
a complicated function of  .
.
Instead of 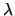 we may equivalently use the log-likelihood
we may equivalently use the log-likelihood
In this case the rejection region will be
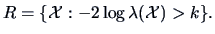 What is the distribution of
What is the distribution of 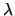 or of
or of
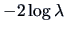 from which we need to compute
from which we need to compute 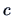 or
or 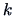 ?
?
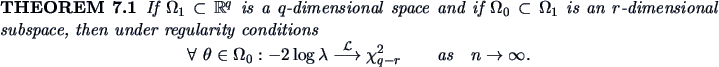
An asymptotic rejection region can now be given by simply
computing the 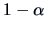 quantile
quantile
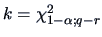 .
The LRT rejection region is therefore
.
The LRT rejection region is therefore
The Theorem 7.1 is thus very helpful: it gives a general way of
building
rejection regions in many problems. Unfortunately, it is only an asymptotic
result, meaning that the size of the test is only approximately equal to
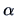 , although the approximation becomes better
when the sample size
, although the approximation becomes better
when the sample size 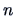 increases. The
question is ``how large should
increases. The
question is ``how large should 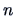 be?''. There is no definite rule:
we encounter here the same problem that was already discussed with respect to
the Central Limit Theorem in Chapter 4.
be?''. There is no definite rule:
we encounter here the same problem that was already discussed with respect to
the Central Limit Theorem in Chapter 4.
Fortunatelly, in many standard circumstances, we can derive exact tests even for
finite samples because the test statistic
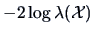 or a simple transformation of it turns out to
have a simple form. This is the case in most of the following standard testing
problems. All of them can be viewed as an illustration of the likelihood
ratio principle.
or a simple transformation of it turns out to
have a simple form. This is the case in most of the following standard testing
problems. All of them can be viewed as an illustration of the likelihood
ratio principle.
Test Problem 1 is an amuse-bouche: in testing the mean of a
multinormal population with a known covariance matrix the likelihood ratio
statistic has a very simple quadratic form with a known distribution under
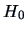 .
.
TEST PROBLEM 1
Suppose that
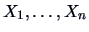 is an i.i.d. random sample
from a
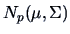 population.
|
In this case 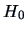 is a simple hypothesis, i.e.,
is a simple hypothesis, i.e.,
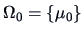 and
therefore the dimension
and
therefore the dimension  of
of  equals
equals 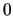 .
Since we have imposed no constraints
in
.
Since we have imposed no constraints
in 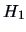 , the space
, the space 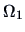 is the whole
is the whole 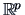 which leads to
which leads to 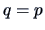 .
From (6.6) we know that
.
From (6.6) we know that
Under 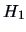 the maximum of
the maximum of
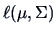 is
is
Therefore,
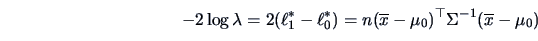 |
(7.2) |
which, by Theorem 4.7, has a 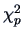 -distribution under
-distribution under 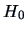 .
.
EXAMPLE 7.2
Consider the bank data again.
Let us test whether the population mean of the forged bank notes is equal to
(This is in fact the sample mean of the genuine bank notes.)
The sample mean of the forged bank notes is
Suppose for the moment that the estimated covariance matrix
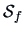
given in (
3.5) is the true covariance matrix
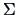
.
We construct the likelihood ratio test and obtain
the quantile
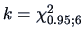
equals
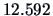
.
The rejection rejection consists of all values in the sample space which
lead to values of the likelihood ratio test statistic larger than
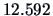
.
Under
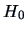
the value of
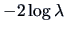
is therefore highly significant.
Hence, the true mean of the forged bank notes is significantly different
from
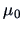
!
Test Problem 2 is the same as the preceding one but in a more realistic
situation where the covariance matrix is unknown: here the
Hotelling's 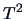 -distribution will be useful to determine an exact test and a
confidence region for the unknown
-distribution will be useful to determine an exact test and a
confidence region for the unknown 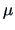 .
.
TEST PROBLEM 2
Suppose that
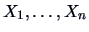 is an i.i.d. random sample from
a
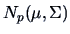 population.
|
Under 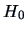 it can be shown that
it can be shown that
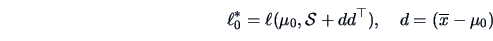 |
(7.3) |
and under 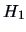 we have
we have
This leads after some calculation to
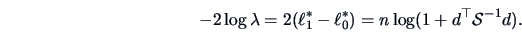 |
(7.4) |
This statistic is a monotone function of
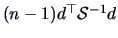 .
This means that
.
This means that
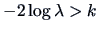 if and only if
if and only if
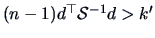 .
The latter statistic has by
Corollary 5.3, under
.
The latter statistic has by
Corollary 5.3, under 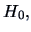 a Hotelling's
a Hotelling's 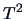 -distribution.
Therefore,
-distribution.
Therefore,
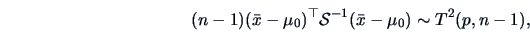 |
(7.5) |
or equivalently
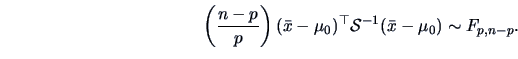 |
(7.6) |
In this case an exact rejection region may be defined as
Alternatively, we have from Theorem 7.1 that
under 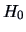 the asymptotic distribution of the test statistic is
the asymptotic distribution of the test statistic is
which leads to the (asymptotically valid) rejection region
but of course, in this case, we would prefer to use the exact 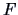 -test
provided just above.
-test
provided just above.
EXAMPLE 7.3
Consider the problem of Example
7.2 again.
We know that
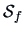
is the empirical analogue for
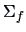
,
the covariance matrix for the forged banknotes.
The test statistic (
7.5) has the value 1153.4 or its equivalent for the
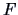
distribution in (
7.6) is 182.5 which is
highly significant (
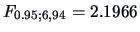
)
so that we conclude that
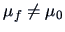
.
Confidence Region for 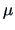
When estimating a multidimensional parameter
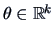 from a
sample, we saw in Chapter 6 how to determine the estimator
from a
sample, we saw in Chapter 6 how to determine the estimator
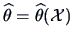 . After the sample is observed
we end up with a point estimate, which is the corresponding observed
value of
. After the sample is observed
we end up with a point estimate, which is the corresponding observed
value of
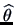 . We know
. We know
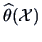 is a random
variable and we often prefer to determine a confidence region
for
is a random
variable and we often prefer to determine a confidence region
for  .
A confidence region (CR) is a random subset of
.
A confidence region (CR) is a random subset of 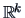 (determined by appropriate statistics) such that we are ``confident'', at
a certain given level
(determined by appropriate statistics) such that we are ``confident'', at
a certain given level 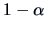 , that this region contains
, that this region contains  :
:
This is just a multidimensional generalization of the basic univariate
confidence interval. Confidence regions are particularly useful when
a hypothesis 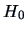 on
on  is rejected, because they help in
eventually identifying which
component of
is rejected, because they help in
eventually identifying which
component of  is responsible for the rejection.
is responsible for the rejection.
There are only a few cases where confidence regions can be easily assessed,
and include most of the testing problems on mean presented in this section.
Corollary 5.3 provides a pivotal quantity which allows
confidence regions for 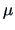 to be constructed.
Since
to be constructed.
Since
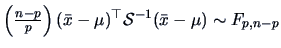 , we have
, we have
Then,
is a confidence region at level (1-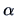 ) for
) for 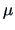 . It is the
interior of an iso-distance ellipsoid in
. It is the
interior of an iso-distance ellipsoid in 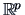 centered at
centered at 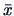 , with a
scaling matrix
, with a
scaling matrix 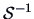 and a distance constant
and a distance constant
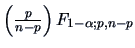 .
When
.
When  is large, ellipsoids are not easy to handle for practical purposes.
One is thus interested in finding confidence intervals for
is large, ellipsoids are not easy to handle for practical purposes.
One is thus interested in finding confidence intervals for
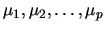 so that simultaneous confidence on all the intervals reaches the desired level
of say,
so that simultaneous confidence on all the intervals reaches the desired level
of say, 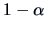 .
.
In the following, we consider a more general problem.
We construct simultaneous confidence intervals for all possible
linear combinations 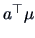 ,
,
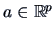 of the elements of
of the elements of 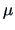 .
.
Suppose for a moment that we fix a particular projection vector 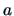 .
We are back to a standard univariate problem of finding a
confidence interval for the mean
.
We are back to a standard univariate problem of finding a
confidence interval for the mean 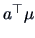 of a univariate random variable
of a univariate random variable
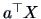 . We can use the
. We can use the 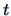 -statistics and
an obvious confidence interval
for
-statistics and
an obvious confidence interval
for 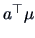 is given by the values
is given by the values 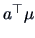 such that
such that
or equivalently
This provides the (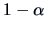 ) confidence interval for
) confidence interval for 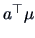 :
:
Now it is easy to prove (using Theorem 2.5) that:
Therefore, simultaneously for all
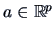 , the interval
, the interval
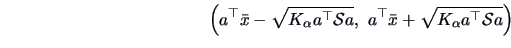 |
(7.7) |
where
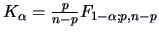 , will contain
, will contain 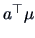 with
probability (
with
probability (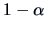 ).
).
A particular choice of 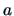 are the columns of the identity matrix
are the columns of the identity matrix
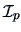 , providing simultaneous confidence
intervals for
, providing simultaneous confidence
intervals for
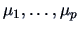 .
We have therefore with probability (
.
We have therefore with probability (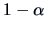 ) for
) for 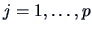
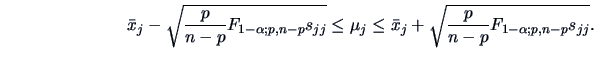 |
(7.8) |
It should be noted that these intervals define a rectangle inscribing
the confidence ellipsoid for 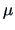 given above. They are particularly useful when a
null hypothesis
given above. They are particularly useful when a
null hypothesis 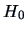 of the type described above is rejected
and one would like
to see which component(s) are mainly responsible for the rejection.
of the type described above is rejected
and one would like
to see which component(s) are mainly responsible for the rejection.
EXAMPLE 7.4
The

confidence region for
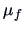
, the mean of the forged banknotes, is given
by the ellipsoid:
The

simultaneous confidence intervals are given by (we use
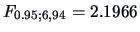
)
Comparing the inequalities with

shows that almost all
components (except the first one) are responsible for the rejection
of
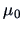
in Example
7.2 and
7.3.
In addition, the method can provide other confidence
intervals. We have at the same level of confidence
(choosing
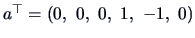 )
)
showing that for the forged bills, the
lower border is essentially smaller than the upper border.
REMARK 7.1
It should be noted that the confidence region is an ellipsoid
whose characteristics depend on the whole matrix
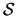
.
In particular, the slope of the axis depends on the eigenvectors of
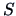
and therefore on the covariances
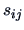
. However, the rectangle inscribing the confidence ellipsoid
provides the simultaneous confidence intervals for
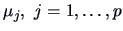
.
They do not depend
on the covariances
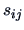
, but only on the variances
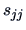
(see (
7.8)).
In particular, it may happen that a tested value
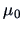
is covered by the intervals (
7.8)
but not covered by the confidence ellipsoid. In this case,
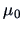
is rejected by a test based on the
confidence ellipsoid but not rejected by a test based on the
simultaneous confidence intervals. The simultaneous confidence
intervals are easier to handle than the full ellipsoid but we have lost
some information, namely the covariance between the components
(see Exercise
7.14).
The following Problem concerns the covariance matrix
in a multinormal population: in this situation
the test statistic has a slightly more complicated
distribution. We will therefore invoke the approximation of Theorem 7.1
in order to derive a test of approximate size 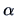 .
.
TEST PROBLEM 3
Suppose that
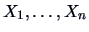 is an i.i.d. random sample
from a
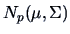 population.
|
Under 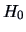 we have
we have
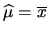 , and
, and
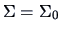 ,
whereas under
,
whereas under 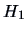 we have
we have
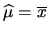 , and
, and
 .
Hence
.
Hence
and thus
Note that this statistic is a function of the eigenvalues of
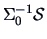 !
Unfortunately, the exact finite sample distribution of
!
Unfortunately, the exact finite sample distribution of 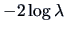 is
very complicated. Asymptotically, we have under
is
very complicated. Asymptotically, we have under 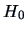
with
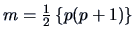 , since a
, since a 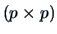 covariance matrix
has only these
covariance matrix
has only these 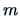 parameters as a consequence of its symmetry.
parameters as a consequence of its symmetry.
EXAMPLE 7.5
Consider the US companies data set (Table
B.5) and suppose we are
interested in the companies of the energy sector, analyzing their assets
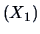
and
sales
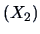
. The sample is of size 15 and provides the value of
![$S=10^7\times \left[\begin{array}{cc}
1.6635 & 1.2410\\
1.2410 & 1.3747
\end{array}\right]$](mvahtmlimg2092.gif)
.
We want to test if
![$\Var {X_1 \choose X_2} = 10^7\times
\left[\begin{array}{cc}
1.2248 & 1.1425\\
1.1425 & 1.5112
\end{array}\right] = \Sigma_0$](mvahtmlimg2093.gif)
.
(
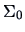
is in fact the empirical variance matrix for

and

for the manufacturing sector).
The test statistic turns out to be
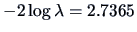
which is not significant for
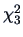
(p-value=0.4341). So we can not conclude that
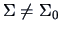
.
In the next testing problem, we address a question that was already stated in
Chapter 3, Section 3.6:
testing a particular value of the coefficients 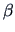 in a linear model. The presentation is done in general terms so that
it can be built on in the next
section where we will test linear restrictions on
in a linear model. The presentation is done in general terms so that
it can be built on in the next
section where we will test linear restrictions on 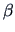 .
.
Under 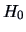 we have
we have
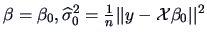 and under
and under 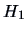 we have
we have
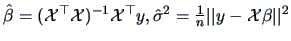 (see Example 6.3).
Hence by Theorem 7.1
(see Example 6.3).
Hence by Theorem 7.1
We draw upon the result (3.45) which gives us:
so that in this case we again have an exact distribution.
EXAMPLE 7.6
Let us consider our ``classic blue'' pullovers again. In Example
3.11 we tried to model the dependency of sales on prices. As
we have seen in Figure
3.5 the slope of the regression curve
is rather small, hence we might ask if
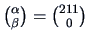
. Here
The test statistic for the LR test is
which under the
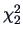
distribution is significant.
The exact
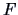
-test statistic
is also significant under the
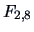
distribution
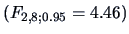
.
Summary

-
The hypotheses
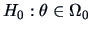 against
against
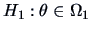 can be tested using the likelihood
ratio test (LRT). The likelihood ratio (LR) is the quotient
can be tested using the likelihood
ratio test (LRT). The likelihood ratio (LR) is the quotient
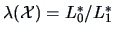 where the
where the 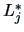 are the
maxima of the likelihood for each of the hypotheses.
are the
maxima of the likelihood for each of the hypotheses.

-
The test statistic in the LRT is
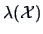 or equivalently
its logarithm
or equivalently
its logarithm
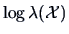 . If
. If 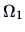 is
is
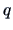 -dimensional and
-dimensional and
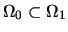
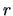 -dimensional,
then the asymptotic distribution of
-dimensional,
then the asymptotic distribution of 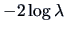 is
is
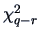 .
This allows
.
This allows 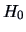 to be tested against
to be tested against 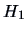 by calculating
the test statistic
by calculating
the test statistic
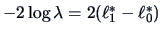 where
where
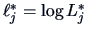 .
.

-
The hypothesis
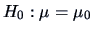 for
for
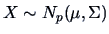 ,
where
,
where 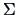 is known, leads to
is known, leads to
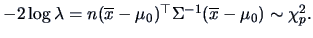

-
The hypothesis
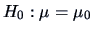 for
for
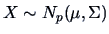 ,
where
,
where 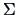 is unknown, leads to
is unknown, leads to
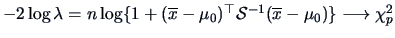 , and
, and
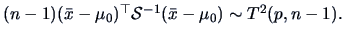

-
The hypothesis
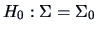 for
for
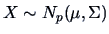 ,
where
,
where 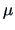 is unknown, leads to
is unknown, leads to
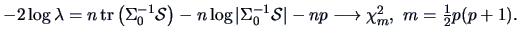

-
The hypothesis
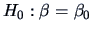 for
for
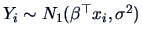 , where
, where 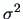 is unknown, leads to
is unknown, leads to
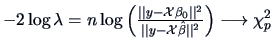 .
.
![]() ,
,
![]() ,
depends on a parameter vector
,
depends on a parameter vector ![]() .
We will consider two hypotheses:
.
We will consider two hypotheses:

![]() corresponds to the ``reduced model'' and
corresponds to the ``reduced model'' and ![]() to the
``full model''. This notation was already used in Chapter 3.
to the
``full model''. This notation was already used in Chapter 3.

![]() ,
the maxima of the likelihood for each of the hypotheses.
Consider the likelihood ratio (LR)
,
the maxima of the likelihood for each of the hypotheses.
Consider the likelihood ratio (LR)

![]() if the LR is high and
if the LR is high and ![]() if the LR is low.
The likelihood ratio test (LRT) tells us when exactly
to favor
if the LR is low.
The likelihood ratio test (LRT) tells us when exactly
to favor ![]() over
over ![]() .
A likelihood ratio test of size
.
A likelihood ratio test of size ![]() for testing
for testing ![]() against
against
![]() has the rejection region
has the rejection region
![]() we may equivalently use the log-likelihood
we may equivalently use the log-likelihood
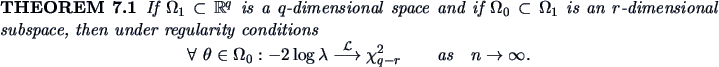
![]() quantile
quantile
![]() .
The LRT rejection region is therefore
.
The LRT rejection region is therefore
![]() or a simple transformation of it turns out to
have a simple form. This is the case in most of the following standard testing
problems. All of them can be viewed as an illustration of the likelihood
ratio principle.
or a simple transformation of it turns out to
have a simple form. This is the case in most of the following standard testing
problems. All of them can be viewed as an illustration of the likelihood
ratio principle.
![]() .
. ![]() is a simple hypothesis, i.e.,
is a simple hypothesis, i.e.,
![]() and
therefore the dimension
and
therefore the dimension ![]() of
of ![]() equals
equals ![]() .
Since we have imposed no constraints
in
.
Since we have imposed no constraints
in ![]() , the space
, the space ![]() is the whole
is the whole ![]() which leads to
which leads to ![]() .
From (6.6) we know that
.
From (6.6) we know that
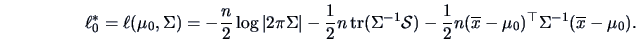
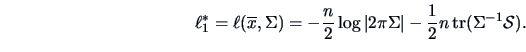
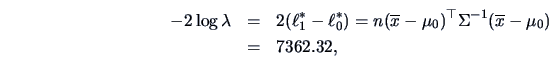
![]() -distribution will be useful to determine an exact test and a
confidence region for the unknown
-distribution will be useful to determine an exact test and a
confidence region for the unknown ![]() .
.
![]() it can be shown that
it can be shown that
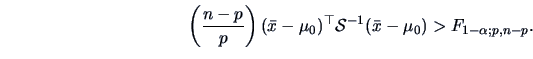
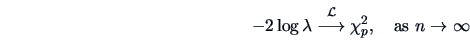
![]() from a
sample, we saw in Chapter 6 how to determine the estimator
from a
sample, we saw in Chapter 6 how to determine the estimator
![]() . After the sample is observed
we end up with a point estimate, which is the corresponding observed
value of
. After the sample is observed
we end up with a point estimate, which is the corresponding observed
value of
![]() . We know
. We know
![]() is a random
variable and we often prefer to determine a confidence region
for
is a random
variable and we often prefer to determine a confidence region
for ![]() .
A confidence region (CR) is a random subset of
.
A confidence region (CR) is a random subset of ![]() (determined by appropriate statistics) such that we are ``confident'', at
a certain given level
(determined by appropriate statistics) such that we are ``confident'', at
a certain given level ![]() , that this region contains
, that this region contains ![]() :
:
![]() to be constructed.
Since
to be constructed.
Since
![]() , we have
, we have
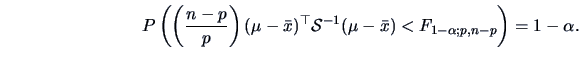
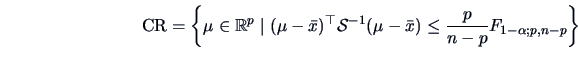
![]() ,
,
![]() of the elements of
of the elements of ![]() .
.
![]() .
We are back to a standard univariate problem of finding a
confidence interval for the mean
.
We are back to a standard univariate problem of finding a
confidence interval for the mean ![]() of a univariate random variable
of a univariate random variable
![]() . We can use the
. We can use the ![]() -statistics and
an obvious confidence interval
for
-statistics and
an obvious confidence interval
for ![]() is given by the values
is given by the values ![]() such that
such that
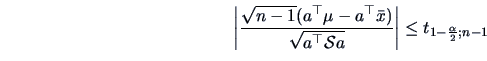
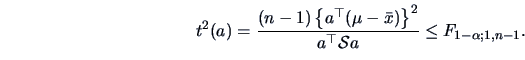
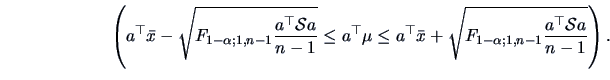
![]() are the columns of the identity matrix
are the columns of the identity matrix
![]() , providing simultaneous confidence
intervals for
, providing simultaneous confidence
intervals for
![]() .
We have therefore with probability (
.
We have therefore with probability (![]() ) for
) for ![]()
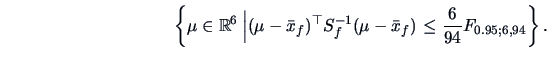

![]() )
)
![]() .
.
![]() we have
we have
![]() , and
, and
![]() ,
whereas under
,
whereas under ![]() we have
we have
![]() , and
, and
![]() .
Hence
.
Hence
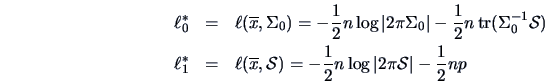
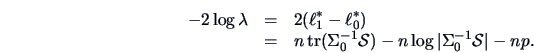
![$S=10^7\times \left[\begin{array}{cc}
1.6635 & 1.2410\\
1.2410 & 1.3747
\end{array}\right]$](mvahtmlimg2092.gif) .
We want to test if
.
We want to test if
![$\Var {X_1 \choose X_2} = 10^7\times
\left[\begin{array}{cc}
1.2248 & 1.1425\\
1.1425 & 1.5112
\end{array}\right] = \Sigma_0$](mvahtmlimg2093.gif) .
(
.
(![]() in a linear model. The presentation is done in general terms so that
it can be built on in the next
section where we will test linear restrictions on
in a linear model. The presentation is done in general terms so that
it can be built on in the next
section where we will test linear restrictions on ![]() .
.
![]() we have
we have
![]() and under
and under ![]() we have
we have
![]() (see Example 6.3).
Hence by Theorem 7.1
(see Example 6.3).
Hence by Theorem 7.1