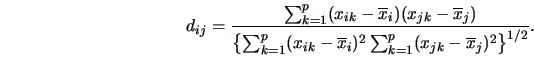11.2 The Proximity between Objects
The starting point of a cluster analysis is a data matrix
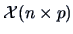 with
with 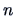 measurements (objects) of
measurements (objects) of  variables. The
proximity (similarity) among objects is described by a
matrix
variables. The
proximity (similarity) among objects is described by a
matrix
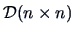
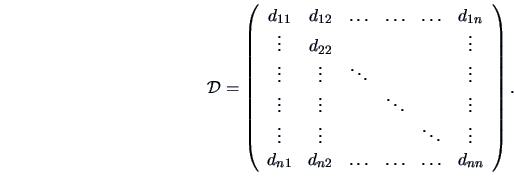 |
(11.1) |
The matrix 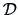 contains measures of similarity or
dissimilarity among the
contains measures of similarity or
dissimilarity among the 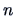 objects. If the values
objects. If the values 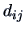 are
distances, then they measure dissimilarity.
The greater the distance, the less similar are the objects. If the
values
are
distances, then they measure dissimilarity.
The greater the distance, the less similar are the objects. If the
values 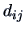 are proximity measures, then the opposite is true, i.e., the greater the
proximity value, the more similar are the objects. A distance matrix,
for example, could be defined by the
are proximity measures, then the opposite is true, i.e., the greater the
proximity value, the more similar are the objects. A distance matrix,
for example, could be defined by the 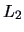 -norm:
-norm:
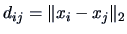 , where
, where 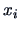 and
and 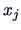 denote the rows of
the data matrix
denote the rows of
the data matrix  .
Distance and similarity are of course dual. If
.
Distance and similarity are of course dual. If 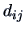 is
a distance, then
is
a distance, then
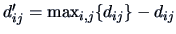 is a proximity
measure.
is a proximity
measure.
The nature of the observations plays an important role in the choice
of proximity measure. Nominal values (like binary variables) lead in
general to proximity values, whereas metric values lead (in general)
to distance matrices. We first present possibilities for 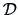 in the binary case and then consider the continuous case.
in the binary case and then consider the continuous case.
Similarity of objects with binary structure
In order to measure the similarity between objects we always compare
pairs of observations
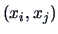 where
where
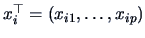 ,
,
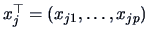 , and
, and
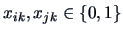 .
Obviously there are four cases:
.
Obviously there are four cases:
Define
Note that each
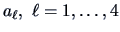 , depends on the
pair
, depends on the
pair
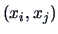 .
.
The following proximity measures are used in practice:
 |
(11.2) |
where 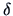 and
and 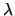 are weighting factors.
Table 11.1 shows some similarity measures for given weighting
factors.
are weighting factors.
Table 11.1 shows some similarity measures for given weighting
factors.
Table 11.1:
The common similarity coefficients.
| Name |
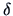 |
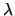 |
Definition |
| Jaccard |
0 |
1 |
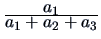 |
| Tanimoto |
1 |
2 |
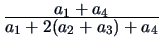 |
| Simple Matching (M) |
1 |
1 |
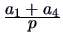 |
| Russel and Rao (RR) |
- |
- |
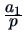 |
| Dice |
0 |
0.5 |
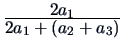 |
| Kulczynski |
- |
- |
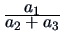 |
|
These measures provide alternative ways of weighting mismatchings and
positive (presence of a common character) or negative (absence of a
common character) matchings.
In principle, we could also consider the Euclidian distance.
However, the disadvantage of this distance is that
it treats the observations 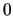 and
and 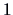 in the same way. If
in the same way. If 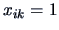 denotes, say,
knowledge of a certain language, then the
contrary,
denotes, say,
knowledge of a certain language, then the
contrary, 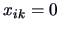 (not knowing the language) should
eventually be treated differently.
(not knowing the language) should
eventually be treated differently.
EXAMPLE 11.1
Let us consider binary variables computed from the car data set (Table
B.7). We define the new binary data by
for
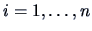
and
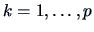
. This means that we transform the
observations of the
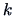
-th variable to
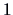
if it is larger than the
mean value of all observations of the
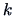
-th variable.
Let us only consider the data points 17 to 19
(Renault 19, Rover and Toyota Corolla) which
lead to
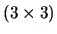
distance matrices.
The Jaccard measure gives the similarity matrix
the Tanimoto measure yields
whereas the Single Matching measure
gives
Distance measures for continuous variables
A wide variety of distance measures can be generated by the
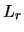 -norms,
-norms, 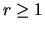 ,
,
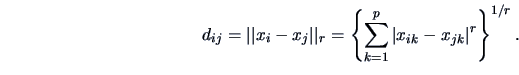 |
(11.3) |
Here 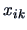 denotes the value of the
denotes the value of the 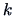 -th variable on object
-th variable on object 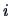 .
It is clear that
.
It is clear that 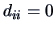 for
for 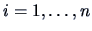 . The class of
distances (11.3) for varying
. The class of
distances (11.3) for varying 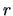 measures the
dissimilarity of different weights. The
measures the
dissimilarity of different weights. The 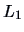 -metric, for example,
gives less weight to outliers than the
-metric, for example,
gives less weight to outliers than the 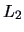 -norm (Euclidean norm).
It is common to consider the squared
-norm (Euclidean norm).
It is common to consider the squared 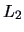 -norm.
-norm.
EXAMPLE 11.2
Suppose we have
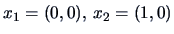
and
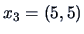
.
Then the distance matrix for the
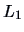
-norm is
and for the squared
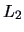
- or Euclidean norm
One can see that the third observation
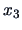
receives much more weight
in the squared
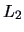
-norm than in the
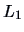
-norm.
An underlying assumption in applying distances based on
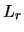 -norms is that the variables are measured on the same scale. If
this is not the case, a standardization should first be applied.
This corresponds to using a more general
-norms is that the variables are measured on the same scale. If
this is not the case, a standardization should first be applied.
This corresponds to using a more general 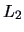 -
or Euclidean norm with a metric
-
or Euclidean norm with a metric 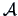 , where
, where 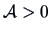 (see Section 2.6):
(see Section 2.6):
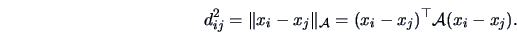 |
(11.4) |
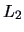 -norms are given by
-norms are given by
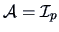 , but if a
standardization is desired, then the weight matrix
, but if a
standardization is desired, then the weight matrix
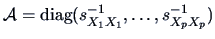 may be
suitable. Recall that
may be
suitable. Recall that
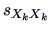 is the variance of the
is the variance of the
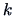 -th component. Hence we have
-th component. Hence we have
 |
(11.5) |
Here each component has the same weight in the computation of the
distances and the distances do not depend on a particular choice of
the units of measure.
EXAMPLE 11.3
Consider the French Food expenditures (Table
B.6).
The Euclidean distance matrix (squared
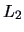
-norm) is
Taking the weight matrix
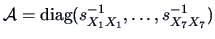
,
we obtain the distance matrix (squared
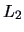
-norm)
 |
(11.6) |
When applied to contingency tables, a 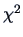 -metric is suitable
to compare (and cluster) rows and columns of a contingency table.
-metric is suitable
to compare (and cluster) rows and columns of a contingency table.
If  is a contingency table, row
is a contingency table, row 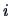 is characterized by
the conditional frequency distribution
is characterized by
the conditional frequency distribution
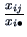 ,
where
,
where
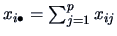 indicates the marginal distributions
over the rows:
indicates the marginal distributions
over the rows:
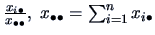 . Similarly, column
. Similarly, column
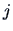 of
of  is characterized by the conditional frequencies
is characterized by the conditional frequencies
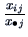 , where
, where
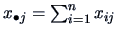 .
The marginal frequencies of the columns are
.
The marginal frequencies of the columns are
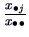 .
.
The distance between two rows, 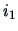 and
and 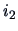 , corresponds to the distance
between their respective frequency distributions. It is common to define this
distance using the
, corresponds to the distance
between their respective frequency distributions. It is common to define this
distance using the 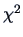 -metric:
-metric:
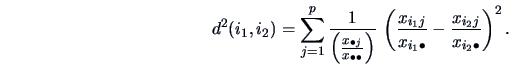 |
(11.7) |
Note that this can be expressed as a distance between the vectors
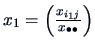 and
and
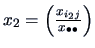 as in (11.4)
with weighting matrix
as in (11.4)
with weighting matrix
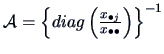 .
Similarly, if we are interested in clusters among the columns, we
can define:
.
Similarly, if we are interested in clusters among the columns, we
can define:
Apart from the Euclidean and the 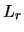 -norm measures one can use
a proximity measure such as the Q-correlation coefficient
-norm measures one can use
a proximity measure such as the Q-correlation coefficient
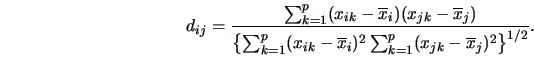 |
(11.8) |
Here
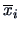 denotes the mean over the variables
denotes the mean over the variables
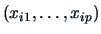 .
.
Summary

-
The proximity between data points is measured by a distance or
similarity matrix
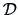 whose components
whose components 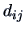 give the
similarity coefficient or the distance between two points
give the
similarity coefficient or the distance between two points 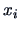 and
and
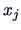 .
.

-
A variety of similarity (distance) measures exist for binary
data (e.g., Jaccard, Tanimoto, Simple Matching coefficients) and
for continuous data (e.g.,
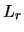 -norms).
-norms).

-
The nature of the data could impose the choice of a particular metric
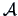 in defining the distances (standardization,
in defining the distances (standardization,
 -metric etc.).
-metric etc.).
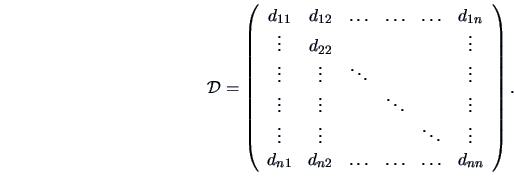
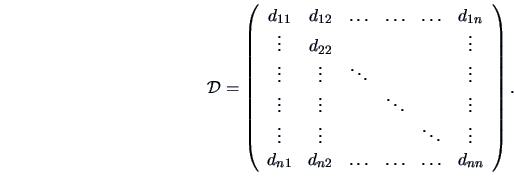
![]() in the binary case and then consider the continuous case.
in the binary case and then consider the continuous case.

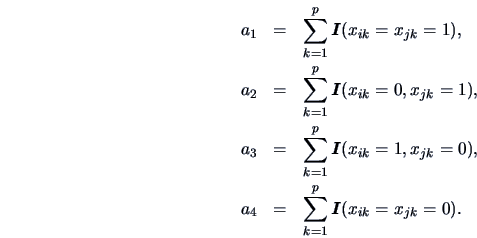
![]() and
and ![]() in the same way. If
in the same way. If ![]() denotes, say,
knowledge of a certain language, then the
contrary,
denotes, say,
knowledge of a certain language, then the
contrary, ![]() (not knowing the language) should
eventually be treated differently.
(not knowing the language) should
eventually be treated differently.

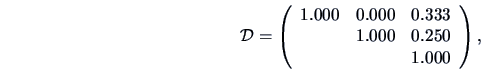
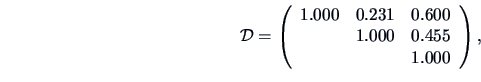
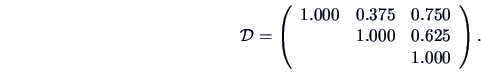
![]() -norms,
-norms, ![]() ,
,


![]() -norms is that the variables are measured on the same scale. If
this is not the case, a standardization should first be applied.
This corresponds to using a more general
-norms is that the variables are measured on the same scale. If
this is not the case, a standardization should first be applied.
This corresponds to using a more general ![]() -
or Euclidean norm with a metric
-
or Euclidean norm with a metric ![]() , where
, where ![]() (see Section 2.6):
(see Section 2.6):


![]() -metric is suitable
to compare (and cluster) rows and columns of a contingency table.
-metric is suitable
to compare (and cluster) rows and columns of a contingency table.
![]() is a contingency table, row
is a contingency table, row ![]() is characterized by
the conditional frequency distribution
is characterized by
the conditional frequency distribution
![]() ,
where
,
where
![]() indicates the marginal distributions
over the rows:
indicates the marginal distributions
over the rows:
![]() . Similarly, column
. Similarly, column
![]() of
of ![]() is characterized by the conditional frequencies
is characterized by the conditional frequencies
![]() , where
, where
![]() .
The marginal frequencies of the columns are
.
The marginal frequencies of the columns are
![]() .
.
![]() and
and ![]() , corresponds to the distance
between their respective frequency distributions. It is common to define this
distance using the
, corresponds to the distance
between their respective frequency distributions. It is common to define this
distance using the ![]() -metric:
-metric:
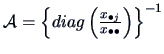 .
Similarly, if we are interested in clusters among the columns, we
can define:
.
Similarly, if we are interested in clusters among the columns, we
can define:
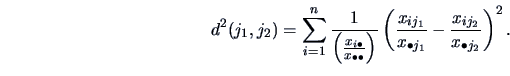
![]() -norm measures one can use
a proximity measure such as the Q-correlation coefficient
-norm measures one can use
a proximity measure such as the Q-correlation coefficient