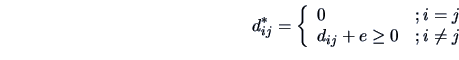Metric MDS begins with a 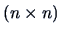 distance matrix
distance matrix 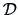 with
elements
with
elements 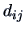 where
where
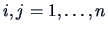 .
The objective of metric MDS is to find a configuration of points in
.
The objective of metric MDS is to find a configuration of points in
 -dimensional space from the distances between the points such that the
coordinates of the
-dimensional space from the distances between the points such that the
coordinates of the 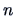 points along the
points along the  dimensions
yield a Euclidean
distance matrix whose elements are as close as possible
to the elements of the given distance matrix
dimensions
yield a Euclidean
distance matrix whose elements are as close as possible
to the elements of the given distance matrix 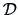 .
.
15.2.1 The Classical Solution
The classical solution is based on a distance matrix that
is computed
from a Euclidean geometry.
DEFINITION 15.1
A
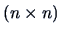
distance matrix
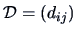
is Euclidean if for some points
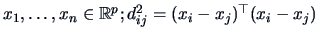
.
The following result tells us whether a distance matrix is Euclidean or
not.
THEOREM 15.1
Define
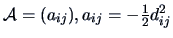
and
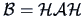
where
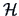
is the centering matrix.
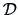
is Euclidean if and only if
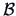
is positive semidefinite.
If
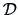
is the distance matrix of a data matrix

, then
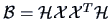
.
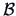
is called the inner product matrix.
The task of MDS is to find the original Euclidean coordinates from
a given distance matrix.
Let the coordinates of 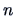 points in a
points in a  dimensional Euclidean
space be given by
dimensional Euclidean
space be given by 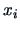 (
(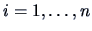 )
where
)
where
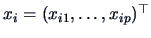 .
Call
.
Call
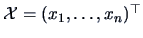 the coordinate matrix and assume
the coordinate matrix and assume
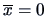 .
The Euclidean distance between the
.
The Euclidean distance between the 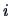 -th and
-th and 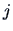 -th points is given by:
-th points is given by:
 |
(15.1) |
The general 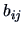 term of
term of 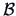 is given by:
is given by:
 |
(15.2) |
It is possible to derive 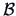 from the known squared distances
from the known squared distances
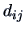 , and then from
, and then from
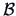 the unknown coordinates.
the unknown coordinates.
Centering of the coordinate matrix 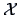 implies that
implies that
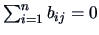 . Summing (15.3) over
. Summing (15.3) over 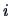 , over
, over 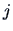 , and over
, and over 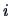 and
and 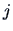 , we find:
, we find:
Solving (15.3) and (15.4) gives:
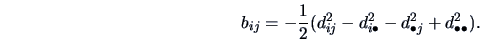 |
(15.5) |
With
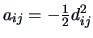 , and
, and
we get:
 |
(15.7) |
Define the matrix 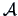 as
as 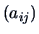 , and observe that:
, and observe that:
 |
(15.8) |
The inner product matrix 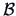 can be expressed as:
can be expressed as:
 |
(15.9) |
where
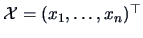 is the
is the 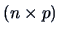 matrix
of coordinates.
The rank of
matrix
of coordinates.
The rank of 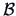 is then
is then
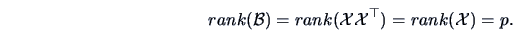 |
(15.10) |
As required in Theorem 15.1 the matrix 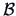 is symmetric,
positive semidefinite and of
rank
is symmetric,
positive semidefinite and of
rank  , and hence it has
, and hence it has  non-negative eigenvalues and
non-negative eigenvalues and 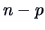 zero
eigenvalues.
zero
eigenvalues.
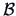 can now be written as:
can now be written as:
 |
(15.11) |
where
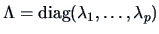 , the diagonal
matrix of the eigenvalues of
, the diagonal
matrix of the eigenvalues of
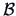 , and
, and
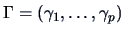 , the matrix
of corresponding eigenvectors.
Hence the coordinate matrix
, the matrix
of corresponding eigenvectors.
Hence the coordinate matrix  containing the point
configuration in
containing the point
configuration in 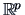 is given by:
is given by:
 |
(15.12) |
The number of desired dimensions is small in order to
provide practical interpretations, and
is given by the rank of 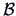 or the number of nonzero
eigenvalues
or the number of nonzero
eigenvalues 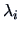 .
If
.
If 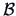 is positive semidefinite, then the
number of nonzero eigenvalues gives the number of eigenvalues required for
representing the distances
is positive semidefinite, then the
number of nonzero eigenvalues gives the number of eigenvalues required for
representing the distances 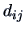 .
.
The proportion of variation explained by  dimensions is given by
dimensions is given by
 |
(15.13) |
It can be used for the choice of  .
If
.
If 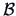 is not positive semidefinite
we can modify (15.13) to
is not positive semidefinite
we can modify (15.13) to
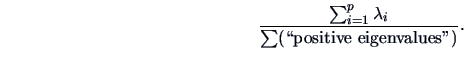 |
(15.14) |
In practice the eigenvalues 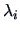 are almost always unequal to zero.
To be able to represent the objects in a space with dimensions
as small as possible we may modify the distance matrix to:
are almost always unequal to zero.
To be able to represent the objects in a space with dimensions
as small as possible we may modify the distance matrix to:
 |
(15.15) |
with
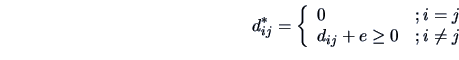 |
(15.16) |
where 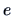 is determined such that the inner product matrix
is determined such that the inner product matrix 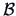 becomes
positive semidefinite with a small rank.
In some situations we do not start with distances but
with similarities.
The standard transformation (see Chapter 11)
from a similarity matrix
becomes
positive semidefinite with a small rank.
In some situations we do not start with distances but
with similarities.
The standard transformation (see Chapter 11)
from a similarity matrix 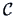 to a distance matrix
to a distance matrix
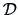 is:
is:
 |
(15.17) |
THEOREM 15.2
If
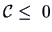
, then the distance matrix
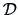
defined by
(
15.17)
is Euclidean with centered inner product matrix
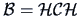
.
Suppose that the (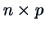 ) data matrix
) data matrix  is centered so
that
is centered so
that
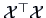 equals a multiple of the covariance matrix
equals a multiple of the covariance matrix 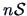 .
Suppose that the
.
Suppose that the  eigenvalues
eigenvalues
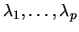 of
of
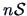 are distinct and non zero. Using the duality
Theorem 8.4 of factorial analysis
we see that
are distinct and non zero. Using the duality
Theorem 8.4 of factorial analysis
we see that
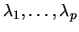 are also eigenvalues of
are also eigenvalues of
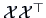 =
= 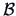 when
when 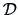 is the Euclidean distance matrix
between the rows of
is the Euclidean distance matrix
between the rows of  . The
. The 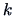 -dimensional solution
to the metric MDS problem is thus given by the
-dimensional solution
to the metric MDS problem is thus given by the 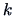 first principal components
of
first principal components
of  .
.
Let  be a
be a 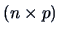 data matrix with some inter-point
distance matrix
data matrix with some inter-point
distance matrix 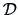 . The objective of MDS is thus to find
. The objective of MDS is thus to find
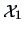 , a representation of
, a representation of  in a lower dimensional
Euclidean space
in a lower dimensional
Euclidean space
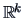 whose inter-point distance matrix
whose inter-point distance matrix 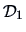 is not far from
is not far from 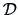 . Let
. Let
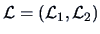 be a
be a 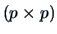 orthogonal matrix where
orthogonal matrix where 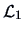 is
is 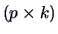 .
.
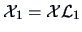 represents a projection
of
represents a projection
of  on the column space of
on the column space of 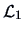 ; in other words,
; in other words,
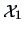 may be viewed as a fitted configuration of
may be viewed as a fitted configuration of  in
in
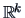 . A measure of discrepancy between
. A measure of discrepancy between 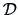 and
and
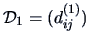 is given by
is given by
 |
(15.18) |
THEOREM 15.3
Among all projections
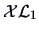
of

onto
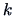
-dimensional
subspaces of
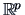
the quantity
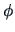
in (
15.18) is
minimized when

is projected onto its first
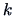
principal factors.
We see therefore that the metric MDS is identical to principal factor analysis
as we have defined it in Chapter 8.
Summary

-
Metric MDS starts with a distance matrix
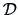 .
.

-
The aim of metric MDS is to construct a map in Euclidean space that corresponds
to the given distances.

-
A practical algorithm is given as:
- start with distances
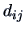
- define
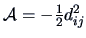
- put
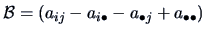
- find the eigenvalues
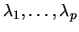 and the associated
eigenvectors
and the associated
eigenvectors
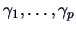 where the eigenvectors are normalized
so that
where the eigenvectors are normalized
so that
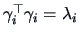 .
.
- Choose an appropriate number of dimensions
 (ideally
(ideally 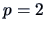 )
)
- The coordinates of the
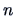 points in the Euclidean space are given by
points in the Euclidean space are given by
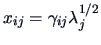 for
for 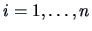 and
and 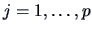 .
.

-
Metric MDS is identical to principal components analysis.
![]() distance matrix
distance matrix ![]() with
elements
with
elements ![]() where
where
![]() .
The objective of metric MDS is to find a configuration of points in
.
The objective of metric MDS is to find a configuration of points in
![]() -dimensional space from the distances between the points such that the
coordinates of the
-dimensional space from the distances between the points such that the
coordinates of the ![]() points along the
points along the ![]() dimensions
yield a Euclidean
distance matrix whose elements are as close as possible
to the elements of the given distance matrix
dimensions
yield a Euclidean
distance matrix whose elements are as close as possible
to the elements of the given distance matrix ![]() .
.
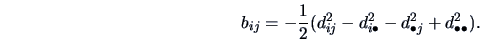
![]() dimensions is given by
dimensions is given by
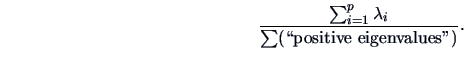
![]() are almost always unequal to zero.
To be able to represent the objects in a space with dimensions
as small as possible we may modify the distance matrix to:
are almost always unequal to zero.
To be able to represent the objects in a space with dimensions
as small as possible we may modify the distance matrix to: