One of the simplest stochastic processes is an ordinary
random walk, a process
whose increments
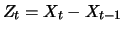 from time
from time 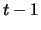 to time
to time 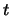 take exclusively the values +1 or -1. Additionally, we assume the
increments to be i.i.d. and independent of the starting value
take exclusively the values +1 or -1. Additionally, we assume the
increments to be i.i.d. and independent of the starting value
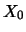 . Hence, the ordinary random walk can be written as:
. Hence, the ordinary random walk can be written as:
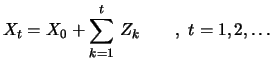 |
(5.1) |
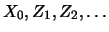 independent and
independent and
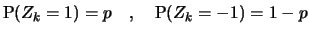
for all
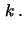
Letting the process go up by 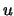 and go down by
and go down by 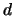 , instead, we
obtain a more general class of binomial
processes:
, instead, we
obtain a more general class of binomial
processes:
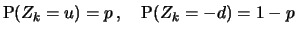
für alle
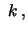
where 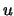 and
and 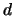 are constant (
are constant (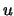 =up,
=up,
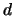 =down).
=down).
Linear interpolation of the points 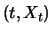 reflects the time
evolution of the process and is called a path of an ordinary
random walk. Starting in
reflects the time
evolution of the process and is called a path of an ordinary
random walk. Starting in 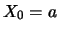 , the process moves on the grid of
points
, the process moves on the grid of
points
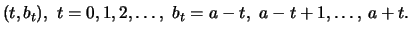 Up to time
Up to time 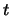 ,
, 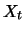 can grow at most
up to
can grow at most
up to 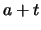 (if
(if
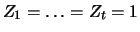 ) or can fall at least to
) or can fall at least to
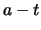 (if
(if
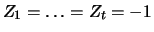 ). Three paths of an ordinary
random walk are shown in Figure 4.1 (
). Three paths of an ordinary
random walk are shown in Figure 4.1 (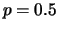 ),
4.2 (
),
4.2 (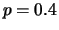 ) and Figure 4.3
(
) and Figure 4.3
(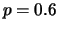 ).
).
Fig.:
Three paths of a symmetric ordinary random walk. (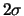 )-intervals
around the drift (which is zero) are given as well.
)-intervals
around the drift (which is zero) are given as well.
 SFEBinomp.xpl
SFEBinomp.xpl
|
|
Fig.:
Three paths of an ordinary random walk with 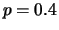 . (
. (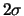 )-intervals around
the drift (which is the line with negative slope) are given as well.
)-intervals around
the drift (which is the line with negative slope) are given as well.
 SFEBinomp.xpl
SFEBinomp.xpl
|
|
Fig.:
Three paths of an ordinary random walk with 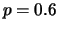 . (
. (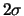 )-intervals around
the drift (which is the line with positive slope) are given as well.
)-intervals around
the drift (which is the line with positive slope) are given as well.
 SFEBinomp.xpl
SFEBinomp.xpl
|
|
For generalized binomial processes the grid of possible paths is
more complicated. The values which the process 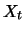 starting in
starting in
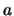 can possibly take up to time
can possibly take up to time 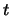 are given by
are given by
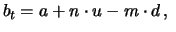
where
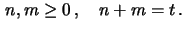
If, from time 0 to time 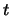 , the process goes up
, the process goes up 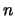 times and
goes down
times and
goes down 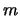 times then
times then
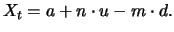 That
is,
That
is, 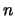 of
of 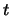 increments
increments
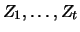 take the value
take the value 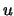 ,
and
,
and 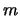 increments take the value
increments take the value 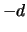 . The grid of possible paths
is also called a binomial tree.
. The grid of possible paths
is also called a binomial tree.
The mean of the symmetric ordinary random walk
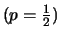 starting
in 0 (
starting
in 0 (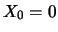 ) is for all times
) is for all times 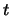 equal to 0 :
equal to 0 :
Otherwise, the random walk has a trend or
drift, for
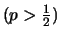 it has a
positive drift and for
it has a
positive drift and for
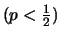 it has a negative
drift. The process grows or falls in average:
it has a negative
drift. The process grows or falls in average:
since it holds for all increments
![$ \mathop{\text{\rm\sf E}}[Z_k] = 2p-1 \, .$](sfehtmlimg528.gif) Hence,
the trend is linear in time. It is the upward sloping line in
Figure 4.3 (
Hence,
the trend is linear in time. It is the upward sloping line in
Figure 4.3 (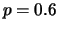 ) and the downward sloping line
in Figure 4.2 (
) and the downward sloping line
in Figure 4.2 (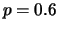 ).
).
For the generalized binomial process with general starting
value 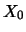 it holds analogously
it holds analogously
![$ \mathop{\text{\rm\sf E}}[Z_k] = (u + d) p - d$](sfehtmlimg529.gif) and
thus:
and
thus:
As time evolves the set of values 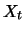 grows, and its variability
increases. Since the summands in (4.1) are independent
and
grows, and its variability
increases. Since the summands in (4.1) are independent
and
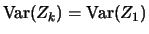 for all
for all 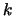 , the variance of
, the variance of 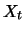 is given by (refer to Section 3.4):
Hence, the variance of
is given by (refer to Section 3.4):
Hence, the variance of 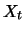 grows linearly with time. So does the
standard deviation. For the random walks depicted in Figure
4.1 (
grows linearly with time. So does the
standard deviation. For the random walks depicted in Figure
4.1 (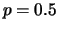 ), Figure 4.2 (
), Figure 4.2 (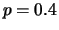 )
and Figure 4.3 (
)
and Figure 4.3 (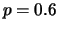 ) the intervals
) the intervals
![$ [\mathop{\text{\rm\sf E}}[X_t] -
2\sigma(X_t); \mathop{\text{\rm\sf E}}[X_t] + 2\sigma(X_t)]$](sfehtmlimg533.gif) are shown as well. For
large
are shown as well. For
large 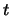 , these intervals should contain 95% of the
realizations of processes.
, these intervals should contain 95% of the
realizations of processes.
The variance of the increments can be easily computed. We use the
following result which holds for the binomial distribution. Define
or
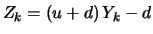 |
(5.2) |
we obtain the following representation of the binomial process
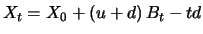 |
(5.3) |
where
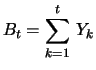 |
(5.4) |
is a 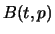 distributed random variable.
distributed random variable.
Given the distribution of 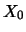 , the distribution of
, the distribution of 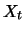 is
specified for all
is
specified for all 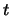 . It can be derived by means of a simple
transformation of the binomial distribution
. It can be derived by means of a simple
transformation of the binomial distribution 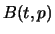 . From
equations (4.2) to (4.4) we obtain for
. From
equations (4.2) to (4.4) we obtain for
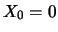 :
:
and for large 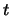 the distribution of
the distribution of 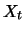 can be approximated
by:
For
can be approximated
by:
For
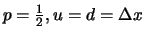 , the following
approximation holds for
, the following
approximation holds for
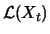 :
:
Figure 4.4 shows the fit for 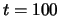 .
.
Fig.:
The distribution of 100 paths of an ordinary symmetric random walk
of length 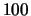 and a kernel density estimation of 100 normally
distributed random variables.
and a kernel density estimation of 100 normally
distributed random variables.
 SFEbinomv.xpl
SFEbinomv.xpl
|
|
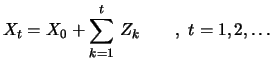
![]() reflects the time
evolution of the process and is called a path of an ordinary
random walk. Starting in
reflects the time
evolution of the process and is called a path of an ordinary
random walk. Starting in ![]() , the process moves on the grid of
points
, the process moves on the grid of
points
![]() Up to time
Up to time ![]() ,
, ![]() can grow at most
up to
can grow at most
up to ![]() (if
(if
![]() ) or can fall at least to
) or can fall at least to
![]() (if
(if
![]() ). Three paths of an ordinary
random walk are shown in Figure 4.1 (
). Three paths of an ordinary
random walk are shown in Figure 4.1 (![]() ),
4.2 (
),
4.2 (![]() ) and Figure 4.3
(
) and Figure 4.3
(![]() ).
).
![\includegraphics[width=1\defpicwidth]{binomp1.ps}](sfehtmlimg514.gif)
![\includegraphics[width=1\defpicwidth]{binomp2.ps}](sfehtmlimg515.gif)
![\includegraphics[width=1\defpicwidth]{binomp3.ps}](sfehtmlimg516.gif)
![]() starting in
starting in
![]() can possibly take up to time
can possibly take up to time ![]() are given by
are given by
![]() , the process goes up
, the process goes up ![]() times and
goes down
times and
goes down ![]() times then
times then
![]() That
is,
That
is, ![]() of
of ![]() increments
increments
![]() take the value
take the value ![]() ,
and
,
and ![]() increments take the value
increments take the value ![]() . The grid of possible paths
is also called a binomial tree.
. The grid of possible paths
is also called a binomial tree.
![]() starting
in 0 (
starting
in 0 (![]() ) is for all times
) is for all times ![]() equal to 0 :
equal to 0 :
![]() it has a
positive drift and for
it has a
positive drift and for
![]() it has a negative
drift. The process grows or falls in average:
it has a negative
drift. The process grows or falls in average:
![]() it holds analogously
it holds analogously
![]() and
thus:
and
thus:
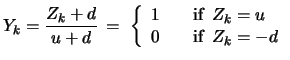
![]() , the distribution of
, the distribution of ![]() is
specified for all
is
specified for all ![]() . It can be derived by means of a simple
transformation of the binomial distribution
. It can be derived by means of a simple
transformation of the binomial distribution ![]() . From
equations (4.2) to (4.4) we obtain for
. From
equations (4.2) to (4.4) we obtain for
![]() :
:
![]() .
.
![\includegraphics[width=1\defpicwidth]{binomv.ps}](sfehtmlimg545.gif)