The moving average process of order 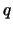 , MA(
, MA(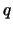 ), is defined as
), is defined as
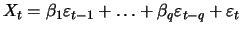 |
(12.1) |
with white noise
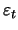 . With the Lag-Operator
. With the Lag-Operator 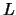 (see
Definition 10.13) instead of (11.1) we can write
(see
Definition 10.13) instead of (11.1) we can write
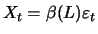 |
(12.2) |
with
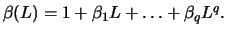 The MA(
The MA(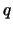 )
process is stationary, since it is formed as the linear
combination of a stationary process. The mean function is simply
)
process is stationary, since it is formed as the linear
combination of a stationary process. The mean function is simply
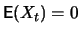 . Let
. Let 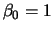 , then the covariance structure is
, then the covariance structure is
For the ACF we have for
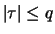
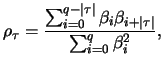 |
(12.3) |
and
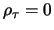 for
for
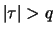 , i.e., the ACF breaks off after
, i.e., the ACF breaks off after
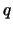 lags.
lags.
As an example consider the MA(1) process
which according to (11.3) holds that
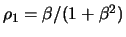 and
and
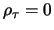 for
for 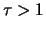 . Figure
11.1 shows the correleogram of a MA(1) process.
. Figure
11.1 shows the correleogram of a MA(1) process.
Fig.:
ACF of a MA(1) process with 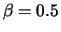 (left)
and
(left)
and
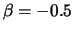 (right).
(right).
 SFEacfma1.xpl
SFEacfma1.xpl
|
|
Obviously the process
has the same ACF, and it holds that
In other words the process with the parameter 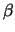 has the same
stochastic properties as the process with the parameter
has the same
stochastic properties as the process with the parameter 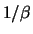 .
This identification problem can be countered by requiring that the
solutions of the characteristic equation
.
This identification problem can be countered by requiring that the
solutions of the characteristic equation
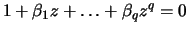 |
(12.4) |
lie outside of the complex unit circle. In this case the linear
filter 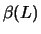 is invertible, i.e., there exists a polynomial
is invertible, i.e., there exists a polynomial
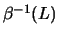 so that
so that
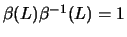 and
and
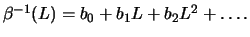 Figure
11.2 displays the correlogram of a MA(2) process
Figure
11.2 displays the correlogram of a MA(2) process
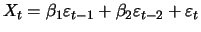 for some collections of parameters.
for some collections of parameters.
Fig.:
ACF of a MA(2) process with
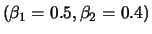 (top left),
(top left),
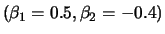 (top right),
(top right),
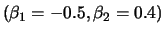 (bottom left) and
(bottom left) and
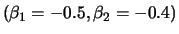 (bottom right).
(bottom right).
 SFEacfma2.xpl
SFEacfma2.xpl
|
|
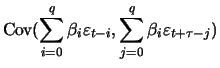
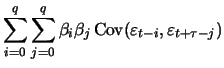
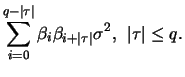
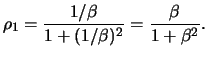
![]() Figure
11.2 displays the correlogram of a MA(2) process
Figure
11.2 displays the correlogram of a MA(2) process
![]() for some collections of parameters.
for some collections of parameters.
![\includegraphics[width=0.5\defpicwidth]{acfma21.ps}](sfehtmlimg2006.gif)
![\includegraphics[width=0.5\defpicwidth]{acfma22.ps}](sfehtmlimg2007.gif)
![\includegraphics[width=0.5\defpicwidth]{acfma23.ps}](sfehtmlimg2008.gif)
![\includegraphics[width=0.5\defpicwidth]{acfma24.ps}](sfehtmlimg2009.gif)