A stochastic process
At a specific time point ![]() ,
, ![]() is a random variable with a
specific density function. Given a specific
is a random variable with a
specific density function. Given a specific
![]() ,
,
![]() is a realization or a
path of the process.
is a realization or a
path of the process.
The stochastic process ![]() is clearly identified, when the
system of its density functions is known. If for any
is clearly identified, when the
system of its density functions is known. If for any
![]() the joint distribution function
the joint distribution function
![]() is known, the underlying
stochastic process is uniquely determined.
is known, the underlying
stochastic process is uniquely determined.
Next we will define moment functions of real stochastic process. Here we will assume that the moments exist. If this is not the case, then the corresponding function is not defined.
In general ![]() depends on time
depends on time ![]() , as, for example, processes
with a seasonal or periodical structure or processes with a
deterministic trend.
, as, for example, processes
with a seasonal or periodical structure or processes with a
deterministic trend.
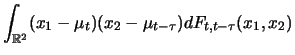 |
(11.2) |
The autocovariance function is symmetric, i.e.,
![]() . For the special case
. For the special case ![]() the result is
the variance function
the result is
the variance function
![]() . In general
. In general
![]() is dependent on
is dependent on ![]() as well as on
as well as on ![]() . In the
following we define the important concept of stationarity, which
will simplify the moment functions in many cases.
. In the
following we define the important concept of stationarity, which
will simplify the moment functions in many cases.
A stochastic process ![]() is strictly stationary if for any
is strictly stationary if for any
![]() and for all
and for all
![]() it holds that
it holds that
For covariance stationary the term weakly stationary is often used. One should notice, however, that a stochastic process can be strictly stationary without being covariance stationary, namely then, when the variance (or covariance) does not exist. If the first two moment functions exist, then covariance stationary follows from strictly stationary.
The ACF is normalized on the interval [-1,1] and thus simplifies
the interpretation of the autocovariance structure from various
stochastic processes. Since the process is required to be
covariance stationary, the ACF depends only on one parameter, the
lag ![]() . Often the ACF is plotted as a function of
. Often the ACF is plotted as a function of ![]() , the
so called correlogram. This is an important graphical
instrument to illustrate linear dependency structures of the
process.
, the
so called correlogram. This is an important graphical
instrument to illustrate linear dependency structures of the
process.
Next we define two important stochastic processes which build the foundation for further modelling.
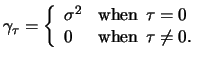
If ![]() is a process from i.i.d. random values with expectation 0
and finite variance, then it is a white noise. This special case
is called independent white noise. On the contrary the white
noise could have dependent third or higher moments, and in this
case it would not be independent.
is a process from i.i.d. random values with expectation 0
and finite variance, then it is a white noise. This special case
is called independent white noise. On the contrary the white
noise could have dependent third or higher moments, and in this
case it would not be independent.
If ![]() is not zero, then the variables
is not zero, then the variables
![]() have a non-zero mean. We call it a random walk with
a drift (see Section 4.1). In contrast to Section
4.3 we do not require here that the variables are
independent. The random walk defined here is the boundary case for
an AR(1) process introduced in Example 10.1 as
have a non-zero mean. We call it a random walk with
a drift (see Section 4.1). In contrast to Section
4.3 we do not require here that the variables are
independent. The random walk defined here is the boundary case for
an AR(1) process introduced in Example 10.1 as
![]() . When we require, as in Section 4.3,
that
. When we require, as in Section 4.3,
that
![]() is independent white noise, then we will call
is independent white noise, then we will call
![]() a random walk with independent increments. Historically the
random walk plays a special role, since at the beginning of the
last century it was the first stochastic model to represent the
development of stock prices. Even today the random walk is often
assumed as an underlying hypothesis. However the applications are
rejected in its strongest form with independent increments.
a random walk with independent increments. Historically the
random walk plays a special role, since at the beginning of the
last century it was the first stochastic model to represent the
development of stock prices. Even today the random walk is often
assumed as an underlying hypothesis. However the applications are
rejected in its strongest form with independent increments.
In order to determine the moment functions of a random walk, we
will simply assume that the constant ![]() and the initial value
and the initial value
![]() are set to zero. Then through recursive substitutions we
will get the representation
are set to zero. Then through recursive substitutions we
will get the representation
| (11.3) |
and for the variance function, since there is no correlation of
![]() , we obtain
, we obtain
The variance of the random walk increases linearly with time. For
the autocovariance function the following holds for ![]() :
:
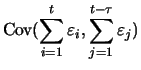 |
|||
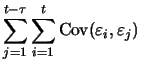 |
|||
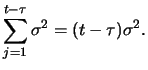 |
For ![]() the autocovariance is thus strictly positive. Since
the covariance function depends on time
the autocovariance is thus strictly positive. Since
the covariance function depends on time ![]() (and not only on the
lags
(and not only on the
lags ![]() ), the random walk is not covariance stationary. For
the autocorrelation function
), the random walk is not covariance stationary. For
the autocorrelation function ![]() we obtain
we obtain
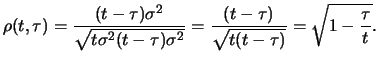
As further illustration we consider a simple, but important stochastic process.
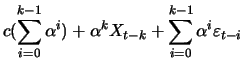 |
|||
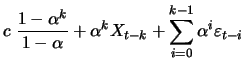 |
If ![]() is given for a particular
is given for a particular ![]() (for example, the
initial value of the process), the characteristics of the process
are obviously dependent on this value. This influence disappears,
however, over time, since we have assumed that
(for example, the
initial value of the process), the characteristics of the process
are obviously dependent on this value. This influence disappears,
however, over time, since we have assumed that
![]() and
thus
and
thus
![]() for
for
![]() . For
. For
![]() there exists a limit in the sense of squared
deviation, thus we can write the process
there exists a limit in the sense of squared
deviation, thus we can write the process ![]() as
as
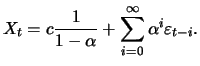
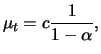
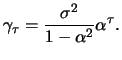
In other words, the conditional distribution of a Markov process at a specific point in time is completely determined by the condition of the system at the previous date. One can also define Markov processes of higher order, from which the conditional distribution only depends on the finite number of past levels. Two examples for the Markov process of first order are the above mentioned random walk with independent variables and the AR(1) process with independent white noise.
Sometimes a fair game is also called a martingale
difference. If ![]() is namely a
martingale, then
is namely a
martingale, then
![]() is a fair game.
is a fair game.
After these mathematical definitions we arrive at the more
econometric definitions, and in particular, at the term return. We
start with a time series of prices
![]() and are
interested in calculating the return between two periods.
and are
interested in calculating the return between two periods.
Should the average return
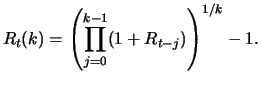
The log return is defined for the case of continuous compounding.
For the average return over several periods we have
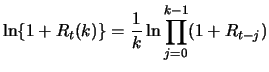 |
|||
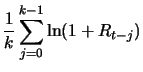 |
|||
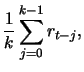 |
For small price changes the difference of the simple return and
log return is negligible. According to the Taylor approximation it
follows that
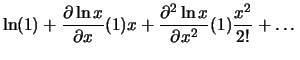 |
|||
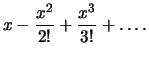 |