Example 12.1 (AR(1))
The AR(1) process from Example
10.1 with
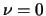
has the
characteristic equation
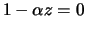
. The explicit solution
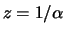
and
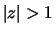
occurs exactly when
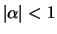
. The
inverse filter of
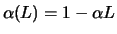
is thus
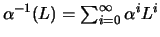
and the
MA(
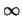
) representation of the AR(1) process is
The ACF of the AR(1) process is
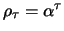
. For
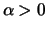
all autocorrelations are positive, for
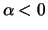
they
alternate between positive and negative, see Figure
11.3.
Example 12.2 (AR(2))
The AR(2) process with
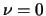
,
is stationary when given the roots
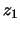
and
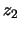
of the
quadratic equation
it holds that
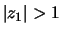
and
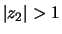
. We obtain solutions as
and
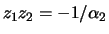
. Due to
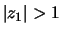
and
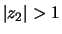
it
holds that
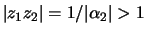
and
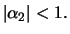 |
(12.11) |
From the Yule-Walker equations in the case of an AR(2) process
it follows that
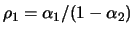
. The case
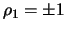
is excluded because a root would lie on the unit circle
(at 1 or -1). Thus for a stationary AR(2) process it must hold
that
from which, together with (
11.11), we obtain the
`stationarity triangle'
i.e., the region in which the AR(2) process is stationary.
The ACF of the AR(2) process is recursively given with
(11.12), (11.13) and
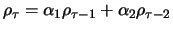 for
for 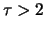 . Figure
(11.4) displays typical patterns.
. Figure
(11.4) displays typical patterns.
![]() , (AR(
, (AR(![]() )), is defined as
)), is defined as
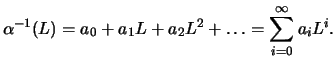
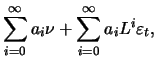
![]() )
process with given parameters is to use the Yule-Walker equations.
They are derived from the definition
of an AR(
)
process with given parameters is to use the Yule-Walker equations.
They are derived from the definition
of an AR(![]() ) process in (11.5) by multiplying by
) process in (11.5) by multiplying by
![]() and taking expectations.
and taking expectations.
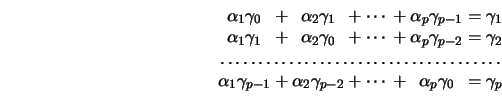
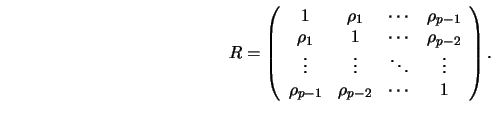
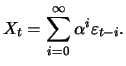
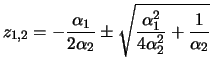
![]() for
for ![]() . Figure
(11.4) displays typical patterns.
. Figure
(11.4) displays typical patterns.![\includegraphics[width=0.5\defpicwidth]{acfar21.ps}](sfehtmlimg2075.gif)
![\includegraphics[width=0.5\defpicwidth]{acfar22.ps}](sfehtmlimg2076.gif)
![\includegraphics[width=0.5\defpicwidth]{acfar23.ps}](sfehtmlimg2077.gif)
![\includegraphics[width=0.5\defpicwidth]{acfar24.ps}](sfehtmlimg2078.gif)