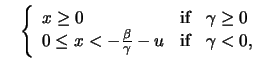Consider the stochastic behavior of the maximum
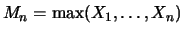 of
of 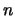 identically distributed random variables
identically distributed random variables
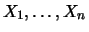 with cumulative distribution function (cdf)
with cumulative distribution function (cdf)
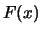 . From a risk management perspective
. From a risk management perspective
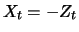 is the
negative return at day
is the
negative return at day  . The cdf of
. The cdf of 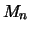 is
is
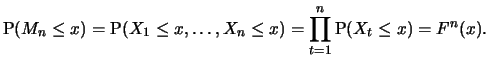 |
(18.1) |
We are only considering unbounded random variables 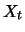 , i.e.
, i.e.
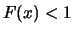 for all
for all
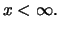 Obviously it holds that
Obviously it holds that
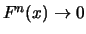 for all
for all 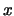 , when
, when
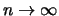 , and thus
, and thus
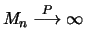 . The maximum of
. The maximum of 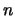 unbounded random variables increases over all boundaries. In order
to achieve a non-degenerate behavior limit,
unbounded random variables increases over all boundaries. In order
to achieve a non-degenerate behavior limit, 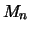 has to be
standardized in a suitable fashion.
has to be
standardized in a suitable fashion.
Definition 18.1 (Maximum Domain of Attraction)
The random variable
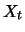
belongs to the
maximum domain of
attraction (MDA) of a non-degenerate distribution
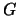
, if for
suitable sequences
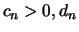
it holds that:
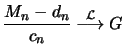
for
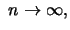
i.e.
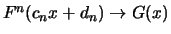
at all continuity points
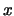
of the cdf
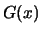
.
It turns out that only a few distributions  can be considered
as the asymptotic limit distribution of the standardized maximum
can be considered
as the asymptotic limit distribution of the standardized maximum
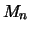 . They are referred to as the extreme value
distriubtions. These are the
following three distribution functions:
. They are referred to as the extreme value
distriubtions. These are the
following three distribution functions:
| Fréchet: |
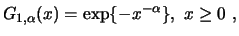 for for
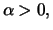 |
| |
|
| Gumbel: |
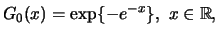 |
| |
|
| Weibull: |
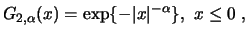 for for
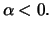 |
Fig.:
Fréchet (red), Gumbel (black) and Weibull distributions (blue).
 SFEevt1.xpl
SFEevt1.xpl
|
|
The Fréchet distributions are concentrated on the
non-negative real numbers
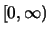 , while the Weibull
distribution, on the other hand, on
, while the Weibull
distribution, on the other hand, on
![$ (- \infty, 0],$](sfehtmlimg3420.gif) whereas the
Gumbel distributed random variables can attain any real number.
Figure 17.1 displays the density function of the Gumbel
distribution, the Fréchet distribution with parameter
whereas the
Gumbel distributed random variables can attain any real number.
Figure 17.1 displays the density function of the Gumbel
distribution, the Fréchet distribution with parameter
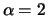 and the Weibull distribution with parameter
and the Weibull distribution with parameter
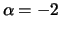 . All three distributions types can be displayed in a
single Mises form:
. All three distributions types can be displayed in a
single Mises form:
Definition 18.2 (Extreme Value Distributions)
The
generalized extreme value distribution (GEV =
generalized extreme value) with the
form parameter
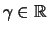
has the distribution function:
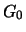 is the Gumbel distribution,
whereas
is the Gumbel distribution,
whereas
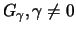 is linked to the Fréchet- and Weibull
distributions by the following
relationships:
is linked to the Fréchet- and Weibull
distributions by the following
relationships:
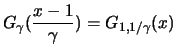
for
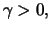
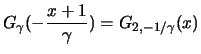
for
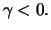
This definition describes the standard
form of the GEV distributions. In general
we can change the center and the scale to obtain other GEV
distributions:
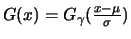 with the
form parameter
with the
form parameter 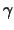 , the location parameter
, the location parameter
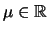 and the scale parameter
and the scale parameter
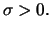 For asymptotic theory this does not matter since the
standardized sequences
For asymptotic theory this does not matter since the
standardized sequences 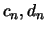 can be always chosen so that
the asymptotic distribution
can be always chosen so that
the asymptotic distribution  has the standard form (
has the standard form (
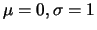 ). An important result of the asymptotic distribution
of the maximum
). An important result of the asymptotic distribution
of the maximum 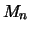 is the Fisher-Tippett
theorem:
is the Fisher-Tippett
theorem:
Theorem 18.1
If there exists sequences
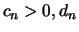
and a non-degenerate
distribution
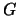
, so that
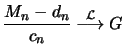
for
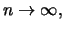
then
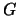
is a GEV distribution.
Proof:
As a form of clarification the basic ideas used to prove this
central result are outlined. Let  , and
, and ![$ [ z ]$](sfehtmlimg3439.gif) represent
the integer part of
represent
the integer part of 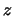 . Since
. Since ![$ F^ {[nt]}$](sfehtmlimg3440.gif) is the distribution
function of
is the distribution
function of ![$ M_{[nt]}$](sfehtmlimg3441.gif) , due to our assumptions on the asymptotic
distribution of
, due to our assumptions on the asymptotic
distribution of 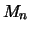 it holds that
On the other hand
it also holds that
it holds that
On the other hand
it also holds that
![$\displaystyle F^ {[nt]} (c_n x + d_n) = \{ F^ n (c_n x + d_n) \} ^ {\frac{[nt]}{n}}
\longrightarrow G^ t (x)\ $](sfehtmlimg3445.gif)
for
In
other words this means that
for
 . According to the Lemma, which is stated below,
this is only possible when
and
. According to the Lemma, which is stated below,
this is only possible when
and
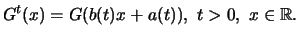 |
(18.2) |
This relationship holds for arbitrary values  . We use it in
particular for arbitrary
. We use it in
particular for arbitrary  and
and  and obtain
and obtain
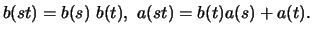 |
(18.3) |
The functional equations (17.2), (17.3) for
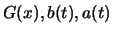 have only one solution, when
have only one solution, when 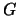 is one of the
distributions
is one of the
distributions
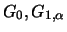 or
or
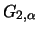 , that is,
, that is,
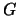 must be a GEV distribution.
must be a GEV distribution.

Lemma 18.1 (Convergence Type Theorem)
Let
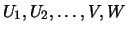
be random variables,
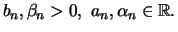
If
in distribution for
, then it holds that:
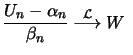
if and only if
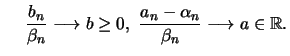
In this case
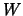
has the same distribution as
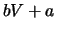
.
Notice that the GEV distributions are identical to the so called
max-stable distributions, by
which for all 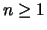 the maximum
the maximum 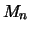 of
of 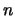 i.i.d. random
variables
i.i.d. random
variables
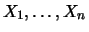 have the same distribution as
have the same distribution as
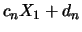 for appropriately chosen
for appropriately chosen
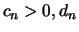 .
.
Fig.:
PP plot for the normal distribution and pseudo random variables with extreme value distributions. Fr'echet (upper left), Weibull (upper right) and Gumbel (below).
 SFEevt2.xpl
SFEevt2.xpl
|
|
Figure 17.2 shows the so called normal plot, i.e., it
compares the graph of the cdf of the normal distribution with the
one in Section 17.2 for the special case
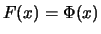 with computer generated random variables that have
a Gumbel distribution, Fréchet distribution with parameter
with computer generated random variables that have
a Gumbel distribution, Fréchet distribution with parameter
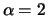 and a Weibull distribution with parameter
and a Weibull distribution with parameter 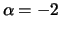 respectively. The differences with the normally distributed
random variables, which would have approximately a straight line
in a normal plot, can be clearly seen.
respectively. The differences with the normally distributed
random variables, which would have approximately a straight line
in a normal plot, can be clearly seen.
If the maximum of i.i.d. random variables converges in
distribution after being appropriately standardized, then the
question arises which of the three GEV distributions is the
asymptotic distribution. The deciding factor is how fast the
probability for extremely large observations decreases beyond a
threshold 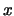 , when
, when 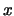 increases. Since this exceedance
probability plays an important role
in extreme value theory, we will introduce some more notations:
increases. Since this exceedance
probability plays an important role
in extreme value theory, we will introduce some more notations:
The relationship between the exceedance probability
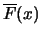 and the distribution of the maxima
and the distribution of the maxima 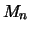 will
become clear with the following theorem.
will
become clear with the following theorem.
Theorem 18.2
a) For
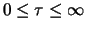
and every sequence of real numbers
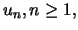
it holds for
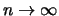
that
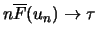
if and only if
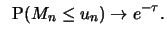
b)

belongs to the maximum domain
of attraction of the GEV distribution
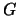
with the standardized
sequences
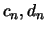
exactly when
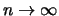
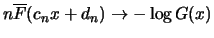
for all
The exceedance probability of the Fréchet distribution
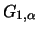 behaves like
behaves like
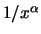 for
for
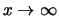 ,
because the exponential function around 0 is approximately linear,
i.e.,
,
because the exponential function around 0 is approximately linear,
i.e.,
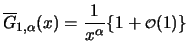
for
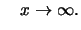
Essentially all of the distributions that belong to the MDA of
this Fréchet distribution show the same behavior;
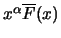 is almost constant for
is almost constant for
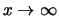 , or more
specifically: a slowly varying function.
, or more
specifically: a slowly varying function.
Definition 18.3
A positive measurable function
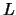
in
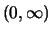
is called
slowly varying, if for all
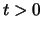
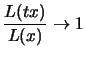
for
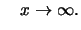
Typical slowly varying functions are, in addition to constants,
logarithmic growth rates, for example
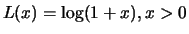 .
.
Theorem 18.3

belongs to the maximum domain of attraction of the Fréchet
distribution
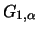
for some
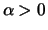
, if and only if
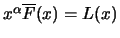
is a slowly varying
function. The random variables
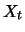
with the distribution
function

are unbounded, i.e.,
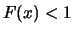
for all
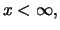
and it holds that
with
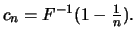
For the description of the standardized sequence 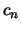 we have
used the following notation.
we have
used the following notation. 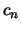 is an extreme quantile of the
distribution
is an extreme quantile of the
distribution  , and it holds that
, and it holds that
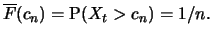
Definition 18.4 (Quantile Function)
If

is a distribution function, we call the generalized inverse
the
quantile function. It then
holds that
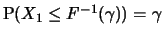
, i.e.,
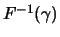
is the
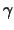
-
quantile
of the distribution

.
If  is strictly monotonic increasing and continuous, then
is strictly monotonic increasing and continuous, then
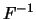 is the generalized inverse of
is the generalized inverse of  .
.
There is a corresponding criterion for the Weibull distribution
that can be shown using the relationship
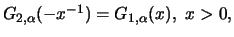 . Random variables, whose maxima are
asymptotically Weibull distributed, are by all means bounded,
i.e., there exists a constant
. Random variables, whose maxima are
asymptotically Weibull distributed, are by all means bounded,
i.e., there exists a constant
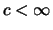 , such that
, such that 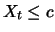 with probability 1. Therefore, in financial applications they are
only interesting in special situations where using a type of
hedging strategy, the loss, which can result from an investment,
is limited. In order to prohibit continuous differentiations in
various cases, in the following we will mainly discuss the case
where the losses are unbounded. The cases in which losses are
limited can be dealt with in a similar fashion.
with probability 1. Therefore, in financial applications they are
only interesting in special situations where using a type of
hedging strategy, the loss, which can result from an investment,
is limited. In order to prohibit continuous differentiations in
various cases, in the following we will mainly discuss the case
where the losses are unbounded. The cases in which losses are
limited can be dealt with in a similar fashion.
Fréchet distributions appear as asymptotic distributions of the
maxima of those random variables whose probability of values
beyond 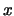 only slowly decreases with
only slowly decreases with 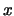 , whereas only bounded
random variables belong to the maximum domain of attraction of
Weibull distributions. Many known distributions such as the
exponential or the normal distribution do not belong to either one
of the groups. It is likely that in such cases the distribution of
the appropriate standardized maxima converges to a Gumbel
distribution. The general conditions need for this are however
more complicated and more difficult to prove than they were for
the Fréchet distribution.
, whereas only bounded
random variables belong to the maximum domain of attraction of
Weibull distributions. Many known distributions such as the
exponential or the normal distribution do not belong to either one
of the groups. It is likely that in such cases the distribution of
the appropriate standardized maxima converges to a Gumbel
distribution. The general conditions need for this are however
more complicated and more difficult to prove than they were for
the Fréchet distribution.
Theorem 18.4
The distribution function

of the unbounded random variables
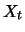
belongs to the maximum domain of attraction of the Gumbel
distribution if measurable scaling functions
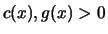
as well as an absolute continuous function
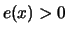
exist with
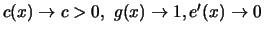
for
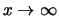
so that for
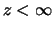
In this case it holds that
with
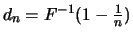
and
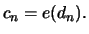
As a function 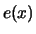 , the average excess
function can be used:
which will be considered in more detail in the following.
, the average excess
function can be used:
which will be considered in more detail in the following.
The exponential distribution with parameter 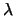 has the
distribution function
has the
distribution function
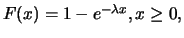 so that
so that
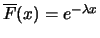 fulfills the
conditions stipulated in the theorem with
fulfills the
conditions stipulated in the theorem with
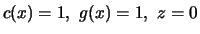 and
and
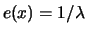 . The maximum
. The maximum 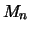 of
of 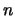 independent exponentially distributed random variables with
parameter
independent exponentially distributed random variables with
parameter 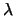 thus converges in distribution to the Gumbel
distribution:
thus converges in distribution to the Gumbel
distribution:
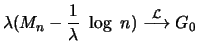
for
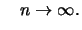
In general, however, the conditions are not so easy to check.
There are other simple sufficient conditions with which it can be
shown, for example, that also the normal distribution belongs to
the maximum domain of attraction of the Gumbel distribution. If,
for example, 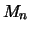 is the maximum of
is the maximum of 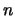 independent standard
normally distributed random variables, then it holds that
independent standard
normally distributed random variables, then it holds that
 SFEevtex1.xpl
SFEevtex1.xpl
Another member of the distributions in the maximum domain of
attraction of the Fréchet distribution
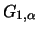 is the
Pareto distribution with the
distribution function
is the
Pareto distribution with the
distribution function
as well as all other distributions with Pareto
tails, i.e., with
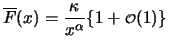
for
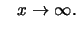
Since
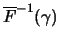 for
for
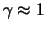 behaves
here like
behaves
here like
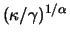 ,
, 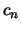 for
for
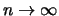 is identical to
is identical to
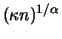 , and
, and
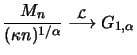
for
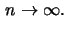
There is a tight relationship between the asymptotic behavior of
the maxima of random variables and the distribution of the
corresponding excesses which builds the foundation for an
important estimation method in the extreme value statistic, which
is defined in the next section. In general it deals with
observations crossing a specified threshold  . Their
distribution
. Their
distribution  is defined as follows:
is defined as follows:
Definition 18.5 (Excess Distribution)
Let

be an arbitrary threshold and

a distribution function
of an unbounded random variable
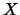
.
- a)
-
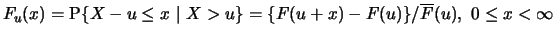 is called the
excess distribution beyond the threshold
is called the
excess distribution beyond the threshold  .
.
- b)
-
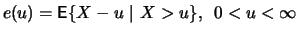 , is the
average excess function.
, is the
average excess function.
With partial integration it follows that this definition of the
average excess function together with the following Theorem
17.4 agrees with:
If  is a random variable with the distribution function
is a random variable with the distribution function
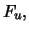 then its expectation is
then its expectation is
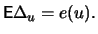
Theorem 18.5
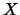
is a positive, unbounded random variable with an absolutely
continuous distribution function

.
a) The average excess function
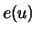
identifies

exactly:
b) If

is contained in the
MDA of the Fréchet distribution
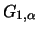
, then
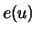
is
approximately linear for
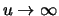
:
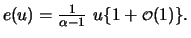
Definition 18.6 (Pareto Distribution)
The
generalized Pareto distribution (GP =
generalized Pareto) with parameters
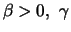
has the distribution function
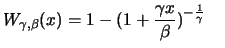
for
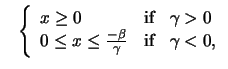
and
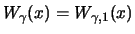
is called the
generalized
standard Pareto distribution or
standardized GP
distribution.
Figure 17.3 shows the generalized standard Pareto distribution
with parameters
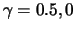 and
and 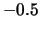 respectively.
respectively.
For
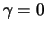 the standardized GP distribution is an exponential distribution with parameter
the standardized GP distribution is an exponential distribution with parameter 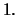 For
For
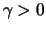 it is a Pareto distribution
it is a Pareto distribution
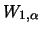 with
the parameter
with
the parameter
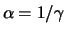 . For
. For
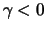 the GP
distribution is also referred to as a Beta distribution and
has the distribution function
the GP
distribution is also referred to as a Beta distribution and
has the distribution function
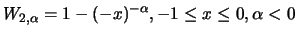 .
.
Fig.:
Standard pareto distribution (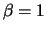 ) with parameter
) with parameter
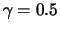 (red),
0 (black) and
(red),
0 (black) and 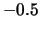 (blue).
(blue).
 SFEgpdist.xpl
SFEgpdist.xpl
|
|
Theorem 18.6
The distribution

is contained in the MDA of the GEV
distribution
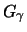
with the form parameter
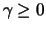
,
exactly when for a measurable function
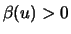
and the GP
distribution
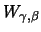
it holds that:
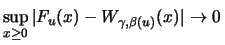
for
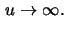
A corresponding result also holds for the case when 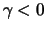 ,
in which case the supremum of
,
in which case the supremum of 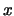 must be taken for those
must be taken for those
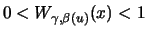 .
.
For the generalized Pareto distribution
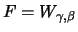 it holds for every finite threshold
it holds for every finite threshold 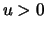
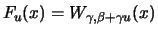
for
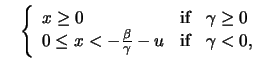
In this case
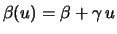 .
.
![]() of
of ![]() identically distributed random variables
identically distributed random variables
![]() with cumulative distribution function (cdf)
with cumulative distribution function (cdf)
![]() . From a risk management perspective
. From a risk management perspective
![]() is the
negative return at day
is the
negative return at day ![]() . The cdf of
. The cdf of ![]() is
is
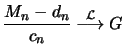 for
for ![]() is the Gumbel distribution,
whereas
is the Gumbel distribution,
whereas
![]() is linked to the Fréchet- and Weibull
distributions by the following
relationships:
is linked to the Fréchet- and Weibull
distributions by the following
relationships:
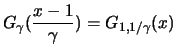 for
for 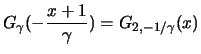 for
for 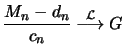 for
for ![$\displaystyle \frac{M_{[nt]} - d_{[nt]}}{c_{[nt]}} \stackrel{{\cal L}}{\longrig...
...\ \, \quad \frac{M_{[nt]} - d_n}{c_n} \stackrel{{\cal L}}{\longrightarrow} G^ t$](sfehtmlimg3446.gif)
![$\displaystyle \frac{c_n}{c_{[nt]}} \longrightarrow b(t) \ge 0,\
\quad \frac{d_n - d_{[nt]}}{c_{[nt]}} \longrightarrow a(t) $](sfehtmlimg3447.gif)
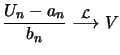
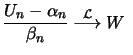 if and only if
if and only if 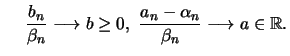
![]() the maximum
the maximum ![]() of
of ![]() i.i.d. random
variables
i.i.d. random
variables
![]() have the same distribution as
have the same distribution as
![]() for appropriately chosen
for appropriately chosen
![]() .
.
![\includegraphics[width=0.4\defpicwidth]{evt21.ps}](sfehtmlimg3463.gif)
![\includegraphics[width=0.4\defpicwidth]{evt22.ps}](sfehtmlimg3464.gif)
![\includegraphics[width=0.4\defpicwidth]{evt23.ps}](sfehtmlimg3465.gif)
![]() , when
, when ![]() increases. Since this exceedance
probability plays an important role
in extreme value theory, we will introduce some more notations:
increases. Since this exceedance
probability plays an important role
in extreme value theory, we will introduce some more notations:
![]() behaves like
behaves like
![]() for
for
![]() ,
because the exponential function around 0 is approximately linear,
i.e.,
,
because the exponential function around 0 is approximately linear,
i.e.,
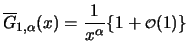 for
for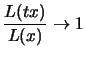 for
for![]() .
.
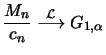
![]() . Random variables, whose maxima are
asymptotically Weibull distributed, are by all means bounded,
i.e., there exists a constant
. Random variables, whose maxima are
asymptotically Weibull distributed, are by all means bounded,
i.e., there exists a constant
![]() , such that
, such that ![]() with probability 1. Therefore, in financial applications they are
only interesting in special situations where using a type of
hedging strategy, the loss, which can result from an investment,
is limited. In order to prohibit continuous differentiations in
various cases, in the following we will mainly discuss the case
where the losses are unbounded. The cases in which losses are
limited can be dealt with in a similar fashion.
with probability 1. Therefore, in financial applications they are
only interesting in special situations where using a type of
hedging strategy, the loss, which can result from an investment,
is limited. In order to prohibit continuous differentiations in
various cases, in the following we will mainly discuss the case
where the losses are unbounded. The cases in which losses are
limited can be dealt with in a similar fashion.
![]() only slowly decreases with
only slowly decreases with ![]() , whereas only bounded
random variables belong to the maximum domain of attraction of
Weibull distributions. Many known distributions such as the
exponential or the normal distribution do not belong to either one
of the groups. It is likely that in such cases the distribution of
the appropriate standardized maxima converges to a Gumbel
distribution. The general conditions need for this are however
more complicated and more difficult to prove than they were for
the Fréchet distribution.
, whereas only bounded
random variables belong to the maximum domain of attraction of
Weibull distributions. Many known distributions such as the
exponential or the normal distribution do not belong to either one
of the groups. It is likely that in such cases the distribution of
the appropriate standardized maxima converges to a Gumbel
distribution. The general conditions need for this are however
more complicated and more difficult to prove than they were for
the Fréchet distribution.
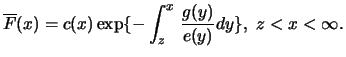
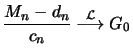
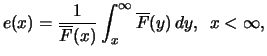
![]() has the
distribution function
has the
distribution function
![]() so that
so that
![]() fulfills the
conditions stipulated in the theorem with
fulfills the
conditions stipulated in the theorem with
![]() and
and
![]() . The maximum
. The maximum ![]() of
of ![]() independent exponentially distributed random variables with
parameter
independent exponentially distributed random variables with
parameter ![]() thus converges in distribution to the Gumbel
distribution:
thus converges in distribution to the Gumbel
distribution:
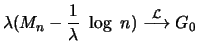 for
for![]() is the maximum of
is the maximum of ![]() independent standard
normally distributed random variables, then it holds that
independent standard
normally distributed random variables, then it holds that
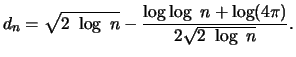
![]() is the
Pareto distribution with the
distribution function
is the
Pareto distribution with the
distribution function

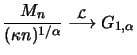 for
for ![]() . Their
distribution
. Their
distribution ![]() is defined as follows:
is defined as follows:
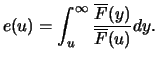
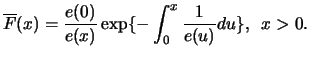
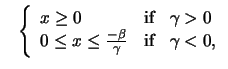
![]() the standardized GP distribution is an exponential distribution with parameter
the standardized GP distribution is an exponential distribution with parameter ![]() For
For
![]() it is a Pareto distribution
it is a Pareto distribution
![]() with
the parameter
with
the parameter
![]() . For
. For
![]() the GP
distribution is also referred to as a Beta distribution and
has the distribution function
the GP
distribution is also referred to as a Beta distribution and
has the distribution function
![]() .
.
![]() it holds for every finite threshold
it holds for every finite threshold ![]()