2.6 Goodness of Fit Measures

As was mentioned in the previous chapter, the measures of goodness of fit are aimed at quantifying how well the OLS regression we have obtained fits the data. The two measures that are usually presented are the standard error of the regression and the $R^{2}$.

In the estimation section, we proved that if the regression model contains intercept, then the sum of the residuals are null (expression 2.32), so the average magnitude of the residuals can be expressed by its sample standard deviation, that is to say, by:

$$\frac{\sum_{i=1}^{n}\hat{u}_{i}^{2}}{n-1}$$

Given the definition of residual, if the regression fits the data well, we should expect it to have a small value. Nevertheless, in the last expression we can substitute $n-1$ by $n-k$, and then, the square of this expression is an unbiased estimator of $\sigma ^{2}$. Thus, we can use the standard error of the regression ($SER$), as a measure of fit:

$$SER=\sqrt{\frac{\sum_{i=1}^{n}\hat{u}_{i}^{2}}{n-k}}=\sqrt{\frac{\hat{u}^{\top }\hat{u}}{n-k}}= \sqrt{\hat{\sigma}^{2}}=\hat{\sigma}$$ (2.128)

In general, the smaller the SER value, the better the regression fits the data. However, in order to establish whether a value is to be considered large or small, we need a reference value. The mean of the endogenous variable $\bar{y}$ can be an adequate reference, given that both are measured in the same units, and then we can obtain the percent of $\bar{y}$ which is represented in $SER$. For example, a $SER$ value of 4 percent of $\bar{y}$ would suggest that the fit seems adequate.

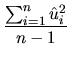
If we want to compare the goodness of fit between two models whose endogenous variables are different, the $R^{2}$ is a more adequate measure than the standard error of the regression, because the $R^{2}$ does not depend on the magnitude of the variables. In order to obtain this measure, we begin, similarly to the univariate linear model by writing the variance decomposition expression, which divides the sample total variation (TSS) in $y$, into the variation which is explained by the model, or explained sum of squares (ESS), and the variation which is not explained by the model, or residual sum of squares (RSS):

$$(y^{D})^{\top }Y^{D}=(\hat{y}^{D})^{\top }\hat{y}^{D}+\hat{u}^{\top }\hat{u} \Rightarrow TSS=ESS+RSS$$ (2.129)

where $\hat{y}^{D}$ is the estimated $y$ vector in deviations, obtained through the matrix $G$, which was defined in (2.40). On this basis, the $R^{2}$ coefficient is defined as:

$$R^{2}=1-\frac{RSS}{TSS}=\frac{ESS}{TSS}$$ (2.130)

which indicates the percentage of the sample total variation in $y$ which is explained by the regression model.

From (2.129) we can deduce that, if the regression explains all the total variation in $y$, then $TSS=ESS$, which implies $R^{2}=1$. However, if the regression explains nothing, then $ESS=0$ and $R^{2}=0$. Thus, we can conclude that $R^{2}$ is bounded between 0 and 1, in such a way that values of it close to one imply a good fit of the regression.

Nevertheless, we should be careful in forming conclusions, because the magnitude of the $R^{2}$ is affected by the kind of data employed in the model. In this sense, when we use time series data and the trends of the endogenous and the explanatory variables are similar, then the $R^{2}$ is usually large, even if there is no strong relationship between these variables. However, when we work with cross-section data , the $R^{2}$ tends to be lower, because there is no trend, and also due to the substantial natural variation in individual behavior. These arguments usually lead the researcher to require a higher value of this measure if the regression is carried out with time series data.

The bounds of the $R^{2}$ we have mentioned do not hold when the estimated model does not contain an intercept. As Patterson (2000) shows, this measure can be larger than one, and even negative. In such cases, we should use an $\textsl{uncentered}$ $R^{2}$ as a measure of fit, which is constructed in a similar way as the $R^{2}$, but where neither $TSS$ nor $ESS$ are calculated by using the variables in deviations, that is to say:

$$R_{u}^{2}=1-\frac{\hat{u}^{\top }\hat{u}}{y^{\top }y}=\frac{\hat{y}^{\top }\hat{y}}{y^{\top }y}$$ (2.131)

In practice, very often several regressions are estimated with the same endogenous variable, and then we want to compare them according to their goodness of fit. For this end, the $R^{2}$ is not valid, because it never decreases when we add a new explanatory variable. This is due to the mathematical properties of the optimization which underly the LS procedure. In this sense, when we increase the number of regressors, the objective function $\hat{u}^{\top }\hat{u}$ decreases or stays the same, but never increases. Using (2.130), we can improve the $R^{2}$ by adding variables to the regression, even if the new regressors do not explain anything about $y$.

In order to avoid this behavior, we compute the so-called adjusted $R^{2}$ $(\bar{R}^{2})$ as:

$$\bar{R}^{2}=1-\frac{\frac{\hat{u}^{\top }\hat{u}}{n-k}}{\frac{(y^{D})^{\top }y^{D}}{n-1}}= 1-\frac{(SER)^{2}}{\frac{(y^{D})^{\top }y^{D}}{n-1}}$$ (2.132)

where $RSS$ and $ESS$ are adjusted by their degrees of freedom.

Given that $TSS$ does not vary when we add a new regressor, we must focus on the numerator of (2.132). When a new variable is added to the set of regressors, then $k$ increases, and both $n-k$ and $\hat{u}^{\top }\hat{u}$ decrease, so we must find out how fast each of them decrease. If the decrease of $n-k$ is less than that of $\hat{u}^{\top }\hat{u}$, then $\bar{R}^{2}$ increases, while it decreases if the reduction of $\hat{u}^{\top }\hat{u}$ is less than that of $n-k$. The $R^{2}$ and $\bar{R}^{2}$ are usually presented in the softwar.

The relationship between $R^{2}$ and $\bar{R}^{2}$ is given by:

$$\bar{R}^{2}=1-\frac{n-1}{n-k}(1-R^{2})$$ (2.133)

where we can see that for $k \geq 1$, $\bar{R}^{2}$ is always less than $R^{2}$, and it can even be negative, so its meaning is not as clear as that of $R^{2}$.

With respect to the $SER$, there is an inverse relationship between it and $\bar{R}^{2}$: if $SER$ increases, then $\bar{R}^{2}$ decreases, and vice versa.

Finally, we should note that these measures should not be used if we are comparing regressions which have a different endogenous variable, even if they are based on the same set of data (for example, $y$ and $\ln y$). Moreover, when we want to evaluate an estimated model, other statistics, together with these measures of fit, must be calculated. These usually refer to the maintenance of the classical assumptions of the MLRM.