Having specified the MLRM given in
(2.1) or (2.2), the following econometric
stage to carry out is the estimation, which consists of
quantifying the parameters of the model, using the observations of
![]() and
and ![]() collected in the sample of size
collected in the sample of size ![]() . The set of
parameters to estimate is
. The set of
parameters to estimate is ![]() : the k coefficients of the vector
: the k coefficients of the vector
![]() , and the dispersion parameter
, and the dispersion parameter
![]() , about which we
have no a priori information.
, about which we
have no a priori information.
Following the same scheme of the previous chapter, we are going to describe the two common estimation procedures: the Least Squares (LS) and the Maximum Likelihood (ML) Methods.
The LS procedure selects those
values of ![]() that minimize the sum of squares of the
distances between the actual values of
that minimize the sum of squares of the
distances between the actual values of ![]() and the adjusted (or
estimated) values of the endogenous variable. Let
and the adjusted (or
estimated) values of the endogenous variable. Let
![]() be a possible estimation (some function of the
sample observations) of
be a possible estimation (some function of the
sample observations) of ![]() . Then, the adjusted value of the
endogenous variable is given by:
. Then, the adjusted value of the
endogenous variable is given by:
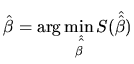 |
(2.20) |
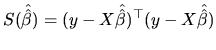 |
(2.21) |
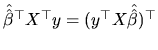 ,
and both elements are
,
and both elements are
From assumption 2 of the last section, we know that ![]() has full
rank, and so we can state that the inverse of
has full
rank, and so we can state that the inverse of
![]() exists, in such a way that we can obtain
exists, in such a way that we can obtain
![]() by
premultiplying (2.24) by
by
premultiplying (2.24) by
![]() :
:
The second-order condition of minimization establishes that the second partial derivatives matrix (hessian matrix) has to be positive definite. In our case, such a matrix is given by:
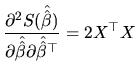 |
(2.27) |
From (2.25), and given that the regressors are fixed, it
follows that
![]() is a linear function of the vector
is a linear function of the vector ![]() ,
that is to say:
,
that is to say:
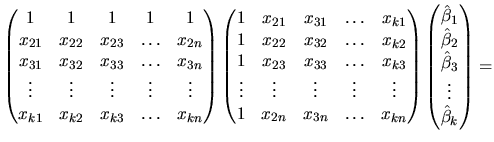
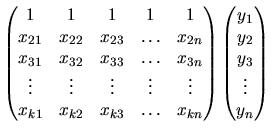
Thus, the ![]() equations which allow us to obtain the unknown
coefficients are the following:
equations which allow us to obtain the unknown
coefficients are the following:
From (2.30) we derive some algebraic properties of the OLS method:
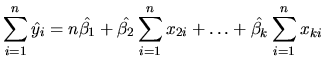
Using (2.31) and (2.18), it is proved that the residuals satisfy:
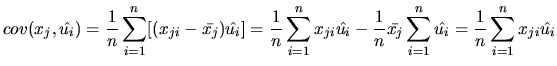
with
![]() . The last expression can be written in matrix
form as:
. The last expression can be written in matrix
form as:
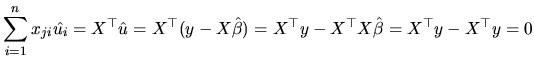
Note that the algebraic property ![]() is always satisfied, while
the properties
is always satisfied, while
the properties ![]() and
and ![]() might not be maintained if the model
has not intercept. This exception can be easily shown, because the
first equation in (2.30) disappears when there is no
constant term.
might not be maintained if the model
has not intercept. This exception can be easily shown, because the
first equation in (2.30) disappears when there is no
constant term.
With respect to the OLS estimation of
![]() , we must note
that it is not obtained as a result of the minimization problem,
but is derived to satisfy two requirements:
, we must note
that it is not obtained as a result of the minimization problem,
but is derived to satisfy two requirements: ![]() to use the OLS
residuals (
to use the OLS
residuals (![]() ), and
), and ![]() to be unbiased. Generalizing the
result of the previous chapter, we have:
to be unbiased. Generalizing the
result of the previous chapter, we have:
An alternative way of obtaining the OLS estimates of the coefficients consists of expressing the variables in deviations with respect to their means; in this case, it can be proved that the value of the estimators and the residuals are the same as that of the previous results. Suppose we have estimated the model, so that we can write it as:
This model called
![]() differs from
(2.35) in two aspects:
differs from
(2.35) in two aspects: ![]() the intercept does not
explicitly appear in the equation model, and
the intercept does not
explicitly appear in the equation model, and ![]() all variables
are expressed in deviations from their means.
all variables
are expressed in deviations from their means.
Nevertheless, researchers are usually interested in evaluating the effect of the explanatory variables on the endogenous variable, so the intercept value is not the main interest, and so, specification (2.37) contains the relevant elements. In spite of this, we can evaluate the intercept later from (2.36), in the following terms:
This approach can be formalized in matrix form, writing (2.35) as:
Consider
![]() a partitioned matrix, and
a partitioned matrix, and
![]() a partitioned
vector, where
a partitioned
vector, where ![]() denotes the
denotes the
![]() matrix whose
columns are the observations of each regressor,
matrix whose
columns are the observations of each regressor, ![]() is an
is an
![]() vector of ones, and
vector of ones, and
![]() is the
is the
![]() vector of all the estimated coefficients except
the intercept.
vector of all the estimated coefficients except
the intercept.
Let ![]() be an
be an ![]() square matrix of the form:
square matrix of the form:
This last expression is the matrix form of (2.37). Now,
we premultiply (2.41) by
![]() , obtaining:
, obtaining:
and taking advantage of the fact that ![]() is also a symmetric
matrix (i.e.,
is also a symmetric
matrix (i.e.,
![]() ), we can rewrite the last expression
as follows:
), we can rewrite the last expression
as follows:
The system of ![]() equations given by (2.44) leads to
the same value of
equations given by (2.44) leads to
the same value of
![]() as that obtained from
(2.24). The only difference between the two systems is
due to the intercept, which is estimated from (2.24),
but not from (2.44). Nevertheless, as we have mentioned
earlier, once we have the values of
as that obtained from
(2.24). The only difference between the two systems is
due to the intercept, which is estimated from (2.24),
but not from (2.44). Nevertheless, as we have mentioned
earlier, once we have the values of
![]() from
(2.44), we can calculate
from
(2.44), we can calculate
![]() through
(2.38). Furthermore, according to (2.41), the
residuals vector is the same as that obtained from
(2.24), so the estimate of
through
(2.38). Furthermore, according to (2.41), the
residuals vector is the same as that obtained from
(2.24), so the estimate of
![]() is that
established in (2.34).
is that
established in (2.34).
Assumption 6 about the normality of the disturbances allows us to
apply the maximum likelihood (ML) criterion to obtain the values
of the unknown parameters of the MLRM. This method consists of the
maximization of the likelihood function, and the values of ![]() and
and
![]() which maximize such a function are the ML
estimates. To obtain the likelihood function, we start by
considering the joint density function of the sample, which
establishes the probability of a sample being realized, when the
parameters are known.
Firstly, we consider a general framework. Let
which maximize such a function are the ML
estimates. To obtain the likelihood function, we start by
considering the joint density function of the sample, which
establishes the probability of a sample being realized, when the
parameters are known.
Firstly, we consider a general framework. Let ![]() be a random vector
which is independently distributed as an n-multivariate normal ,
with expectations vector
be a random vector
which is independently distributed as an n-multivariate normal ,
with expectations vector ![]() , and variance-covariance
matrix
, and variance-covariance
matrix ![]() . The probability density function of
. The probability density function of ![]() is given by:
is given by:
In the framework of the MLRM, the set of classical assumptions
stated for the random component allowed us to conclude that the
![]() vector is distributed as an n-multivariate normal, with
vector is distributed as an n-multivariate normal, with
![]() being the vector of means , and
being the vector of means , and
![]() the
variance-covariance matrix (results (2.15) and
(2.16)). From (2.45) and (2.46), the
likelihood function is:
the
variance-covariance matrix (results (2.15) and
(2.16)). From (2.45) and (2.46), the
likelihood function is:
The ML method maximizes (2.47) in order to obtain the ML
estimators of ![]() and
and
![]() .
.
In general, the way of deriving the likelihood function
(2.47) is based on the relationship between the
probability distribution of ![]() and that of
and that of ![]() . Suppose
. Suppose ![]() and
and
![]() are two random vectors, where
are two random vectors, where ![]() with
with ![]() being a
monotonic function. If we know the probability density function of
being a
monotonic function. If we know the probability density function of
![]() , denoted by
, denoted by ![]() , we can obtain the probability density
function of
, we can obtain the probability density
function of ![]() as follows:
as follows:
Although the ML method maximizes the likelihood function, it is
usually simpler to work with the log of this function. Since the
logarithm is a monotonic function, the parameter values that
maximize L are the same as those that maximize the log-likelihood
(![]() ). In our case,
). In our case, ![]() has the following form:
has the following form:
All estimation quantlets in the stats quantlib have as input parameters:
In the following example, we will use Spanish economic data to
illustrate the MLRM estimation. The file
data.dat
contains
quarterly data from 1980 to 1997 (sample size ![]() ) for the
variables consumption, exports and M1 (monetary supply). All
variables are expressed in constant prices of 1995.
) for the
variables consumption, exports and M1 (monetary supply). All
variables are expressed in constant prices of 1995.
Descriptive statistics of the three variables which are included in the consumption function can be found in the Table 2.1.
|
On the basis of the information on the data file, we estimate the consumption function; the endogenous variable we want to explain is consumption, while exportations and M1 are the explanatory variables, or regressors.
The quantlet XEGmlrm01.xpl produces some summary statistics
The quantlet in the
stats
quantlib which can be employed
to obtain only the OLS (or ML) estimation of the coefficients
![]() and
and
![]() is
is
 gls
.
gls
.
|
In XEGmlrm02.xpl, we have used the quantlet
 gls
to
compute the OLS estimates of
gls
to
compute the OLS estimates of ![]() (b), and both the OLS
and ML estimates of
(b), and both the OLS
and ML estimates of ![]() (sigls and sigml).
(sigls and sigml).