4.1 Introduction

A univariate time series consists of a set of observations on a single variable, $ y$. If there are $ T$ observations, they may be denoted by $ y_t, t=1, 2, \ldots, T$. A univariate time series model for $ y_t $ is formulated in terms of past values of $ y_t $ and/or its position in relation to time.

Time series of economic data display many different characteristics and one easy way of starting the analysis of a series is to display the data by means of a timeplot in which the series of interest is graphed against time. A visual inspection of a time series plot allows us to see the relevant feature of dependence among observations and other important characteristics such as trends (long-run movements of the series), seasonalities, cycles of period longer than a year, structural breaks, conditional heteroskedasticity, etc.

Figure 4.1: Time series plots
\includegraphics[width=1.3\defpicwidth]{4series.ps}

Figure 4.1 shows graphics of four economic time series that exhibit some of these characteristics. The $ Minks$ series plotted in graphic (a) evolves around a constant mean with cycles of period approximately 10 years, while the $ GDP$ series presents an upward trending pattern (graphic (b)) and the $ Tourists $ series is dominated by a cyclical behavior that repeats itself more or less every year and which is called seasonality (graphic (c)). On the other hand, finance time series usually present variances that change over time as can be observed in graphic (d). This behavior can be captured by conditional heteroskedasticity models that will be treated in detail in Chapter 6.

A time series model should reproduce these characteristics but there is no unique model to perform this analysis. With regard to trends and seasonalities, a simple way to deal with them is working within the framework of linear regression models (Diebold; 1997). In these models, the trend is specified as a deterministic function of time about which the series is constrained to move forever. For instance, a simple linear regression model able to represent the trending behaviour of the $ GDP$ series can be formulated as follows:

$\displaystyle y_t = \alpha + \beta t + u_t $

where $ u_t$ is the error term that may be correlated. The variable $ t$ is constructed artificially as a 'dummy variable' that takes the value 1 in the first period of the sample, 2 in the second period and so on.

As far as seasonality is concerned, it can be easily modelled as a deterministic function of time by including in the regression model a set of $ s$ seasonal dummies:

$\displaystyle D_{jt} = \left\{ \begin{array}{ll} 1 & t \in \hbox{ season} \, j \\ 0 & \hbox{otherwise} \\ \end{array} \right. \, \, j = 1, 2, \ldots, s $

where $ s$ is the number of seasons in a year, thus, $ s = 4 $ if we have quarterly data, $ s =12$ if we have monthly data, and so forth. A linear regression model for a time series with a linear trend and seasonal behaviour can be formulated as follows:

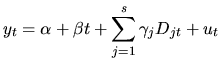
$\displaystyle y_t = \alpha + \beta t + \sum_{j=1}^{s} \gamma_j D_{jt} + u_t $

where $ \gamma_j$ are the seasonal coefficients constrained to sum zero.

This kind of models are very simple and may be easily estimated by least squares. Trends and seasonalities estimated by these models are global since they are represented by a deterministic function of time which holds at all points throughtout the sample. Forecasting is straightforward as well: it consists of extrapolating these global components into the future.

A classical alternative to these models are the Exponential Smoothing Procedures (see Gardner (1985) for a survey). These models are local in the sense that they fit trends and seasonalities placing more weight on the more recent observations. In this way, these methods allow the components to change slowly within the sample and the most recent estimations of these components are extrapolated into the future in forecasting. These models are easy to implement and can be quite effective. However, they are ad hoc models because they are implemented without a properly defined statistical model. A class of unobserved components models that allow trends and seasonalities to evolve in time stochastically may be found in Harvey (1989). Last, modelling time series with trend and/or seasonal behaviour within the ARIMA framework will be presented in section 4.3 and in Chapter 5 respectively.