The models presented so far are based on the stationarity assumption, that
is, the mean and the variance of the underlying process are constant and
the autocovariances depend only on the time lag. But many economic and
business time series are nonstationary. Nonstationary time series can occur
in many different ways. In particular, economic time series usually show
time-changing levels, ![]() , (see graph (b) in figure 4.1)
and/or variances (see graph (c) in figure 4.1).
, (see graph (b) in figure 4.1)
and/or variances (see graph (c) in figure 4.1).
When a time series is not stationary in variance we need a proper variance stabilizing transformation. It is very common for the variance of a nonstationary process to change as its level changes. Thus, let us assume that the variance of the process is:
Thus, the transformation ![]() must be chosen so that:
must be chosen so that:
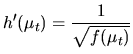
More generally, to stabilize the variance, we can use the power transformation introduced by Box and Cox (1964):
One of the dominant features of many economic and business time series is the trend. Trend is slow, long-run evolution in the variables that we want to model. In business, economics, and finance time series, trend is usually produced by slowly evolving preferences, technologies and demographics. This trend behavior can be upward or downward, steep or not, and exponential or approximately linear. With such a trending pattern, a time series is nonstationary, it does not show a tendency of mean reversion.
Nonstationarity in the mean, that is a non constant level, can be modelled in different ways. The most common alternatives are deterministic trends and stochastic trends.
Let us consider the extension of Wold's decomposition theorem for nonstationary series given by Cramer (1961):
For example, if the mean function ![]() follows a linear trend, one can use the deterministic linear trend model:
follows a linear trend, one can use the deterministic linear trend model:
Sometimes trend appears nonlinear, or curved, as for example when a variable increases at an increasing or decreasing rate. In fact, it is not required that trends be linear only that they be smooth. Quadratic trend models can potentially capture nonlinearities such as those observed in some series. Such trends are quadratic as opposed to linear functions of time,
Thus, trend is a linear function of time. This situation, in which a trend appears nonlinear in levels but linear in logarithms is called exponential trend or log-linear trend and is very common in economics because economic variables often displays roughly constant growth rates.
Nonstationarity in the mean can be dealt within the class of the
![]() models (4.7). An
models (4.7). An ![]() model is
nonstationary if its
model is
nonstationary if its ![]() polynomial does not satisfy the
stationarity condition, that is, if some of its roots do not lie
outside the unit circle. If the
polynomial does not satisfy the
stationarity condition, that is, if some of its roots do not lie
outside the unit circle. If the ![]() polynomial contains at least
one root inside the unit circle, the behavior of a
realization of the process will be explosive. However, this is not
the sort of evolution that can be observed in economic and
business time series. Although many of them are nonstationary,
these series behave very much alike except for their difference in
the local mean levels. If we want to model the evolution of the
series independent of its level within the framework of
polynomial contains at least
one root inside the unit circle, the behavior of a
realization of the process will be explosive. However, this is not
the sort of evolution that can be observed in economic and
business time series. Although many of them are nonstationary,
these series behave very much alike except for their difference in
the local mean levels. If we want to model the evolution of the
series independent of its level within the framework of ![]() models, the
models, the ![]() polynomial must satisfy:
polynomial must satisfy:
Applying this decomposition to the general ![]() model:
model:
where ![]() is a polynomial of order
is a polynomial of order ![]() and
and
![]() . If
. If ![]() is a stationary
is a stationary ![]() polynomial, we say
that
polynomial, we say
that ![]() has a unit autoregressive root. When the nonstationary
has a unit autoregressive root. When the nonstationary
![]() polynomial presents more than one unit root, for instance
polynomial presents more than one unit root, for instance
![]() , it can be decomposed as:
, it can be decomposed as:
In short, if we use ![]() processes for modelling nonstationary
time series, the nonstationarity leads to the presence of unit
roots in the autoregressive polynomial. In other words, the series
processes for modelling nonstationary
time series, the nonstationarity leads to the presence of unit
roots in the autoregressive polynomial. In other words, the series
![]() is nonstationary but its
is nonstationary but its ![]() th differenced series,
th differenced series,
![]() , for some integer
, for some integer ![]() , follows a stationary and
invertible
, follows a stationary and
invertible
![]() model. A process
model. A process ![]() with these
characteristics is called an integrated process of order
d and it is denoted by
with these
characteristics is called an integrated process of order
d and it is denoted by
![]() . It can be noted
that the order of integration of a process is the number of
differences needed to achieve stationarity, i.e., the
number of unit roots present in the process. In practice
. It can be noted
that the order of integration of a process is the number of
differences needed to achieve stationarity, i.e., the
number of unit roots present in the process. In practice ![]() and
and ![]() processes are by far the most important cases for
economic and business time series, arising
processes are by far the most important cases for
economic and business time series, arising ![]() series much less
frequently. Box and Jenkins (1976) refer to this kind of
nonstationary behavior as homogeneous nonstationarity, indicating
that the local behavior of this sort of series is independent of
its level (for
series much less
frequently. Box and Jenkins (1976) refer to this kind of
nonstationary behavior as homogeneous nonstationarity, indicating
that the local behavior of this sort of series is independent of
its level (for ![]() processes) and of its level and slope (for
processes) and of its level and slope (for
![]() processes).
processes).
In general, if the series ![]() is integrated of order
is integrated of order ![]() , it can
be represented by the following model:
, it can
be represented by the following model:
The resulting homogeneous nonstationary model (4.19) has been
referred to as the Autoregressive Integrated Moving Average model of
order ![]() and is denoted as the
and is denoted as the
![]() model. When
model. When ![]() ,
the
,
the
![]() is also called the Integrated Moving Average model of
order
is also called the Integrated Moving Average model of
order ![]() and it is denoted as the
and it is denoted as the ![]() model. When
model. When ![]() , the
resulting model is called the Autoregressive Integrated model
, the
resulting model is called the Autoregressive Integrated model ![]() .
.
In order to get more insight into the kind of nonstationary
behavior implied by integrated processes, let us study with some
detail two of the most simple ![]() models: random walk and random walk
with drift models.
models: random walk and random walk
with drift models.
The random walk model is simply an ![]() with coefficient
with coefficient ![]() :
:
That is, in the random walk model the value of ![]() at time
at time ![]() is
equal to its value at time
is
equal to its value at time ![]() plus a random shock. The random
walk model is not covariance stationary because the
plus a random shock. The random
walk model is not covariance stationary because the ![]() coefficient is not less than one. But since the first difference
of the series follows a white noise process,
coefficient is not less than one. But since the first difference
of the series follows a white noise process, ![]() is an
integrated process of order 1,
is an
integrated process of order 1, ![]() . This model has been widely
used to describe the behavior of finance time series such as stock
prices, exchange rates, etc.
. This model has been widely
used to describe the behavior of finance time series such as stock
prices, exchange rates, etc.
Graph (a) of figure 4.11 shows a simulated realization of size
150 of a random walk process, with
![]() . It can be
observed that the series does not display what is known as a mean reversion
behavior: it wanders up and down randomly with no tendency to return to any
particular point. If a shock increases the value of a random walk, there is
no tendency for it to necessarily lower again, it is expected to stay
permanently higher.
. It can be
observed that the series does not display what is known as a mean reversion
behavior: it wanders up and down randomly with no tendency to return to any
particular point. If a shock increases the value of a random walk, there is
no tendency for it to necessarily lower again, it is expected to stay
permanently higher.
Taking expectations in (4.20) given the past information
![]() , we get:
, we get:
Assuming that the random walk started at some time ![]() with value
with value ![]() ,
we get:
,
we get:
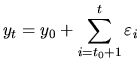
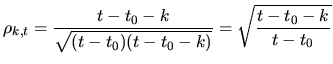
The random walk with drift model results of adding a nonzero constant term to the random walk model:
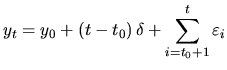
The random walk with drift is a model that on average grows each period by
the drift, ![]() . This drift parameter
. This drift parameter ![]() plays the same role as
the slope parameter in the linear deterministic trend model (4.18).
Just as the random walk has no particular level to which it returns, so
the random walk with drift model has no particular trend to which it
returns. If a shock moves the value of the process below the
currently projected trend, there is no tendency for it to return; a new
trend simply begins from the new position of the series (see graph (b) in
figure 4.11).
plays the same role as
the slope parameter in the linear deterministic trend model (4.18).
Just as the random walk has no particular level to which it returns, so
the random walk with drift model has no particular trend to which it
returns. If a shock moves the value of the process below the
currently projected trend, there is no tendency for it to return; a new
trend simply begins from the new position of the series (see graph (b) in
figure 4.11).
In general, if a process is integrated, that is,
![]() for some
for some ![]() , shocks have completely permanent effects; a unit shock
moves the expected future path of the series by one unit forever. Moreover,
the parameter
, shocks have completely permanent effects; a unit shock
moves the expected future path of the series by one unit forever. Moreover,
the parameter ![]() plays very different roles for
plays very different roles for ![]() and
and ![]() . When
. When
![]() , the process is stationary and the parameter
, the process is stationary and the parameter ![]() is
related to the mean of the process,
is
related to the mean of the process, ![]() :
:
However, when ![]() , the presence of the constant term
, the presence of the constant term ![]() introduces a deterministic linear trend in the process (see graph (b) in
figure 4.11). More generally, for models involving the
introduces a deterministic linear trend in the process (see graph (b) in
figure 4.11). More generally, for models involving the
![]() th differenced series
th differenced series
![]() , the nonzero parameter
, the nonzero parameter ![]() can
be shown to correspond to the coefficient
can
be shown to correspond to the coefficient ![]() of
of ![]() in the
deterministic trend,
in the
deterministic trend,
![]() . That is why, when
. That is why, when ![]() , the parameter
, the parameter ![]() is referred
to as the deterministic trend term. In this case, the models may be
interpreted as including a deterministic trend buried in a nonstationary
noise.
is referred
to as the deterministic trend term. In this case, the models may be
interpreted as including a deterministic trend buried in a nonstationary
noise.
As we have seen the properties of a time series depend on its
order of integration, ![]() , that is on the presence of unit roots.
It is important to have techniques available to determine the
actual form of nonstationarity and to distinguish between
stochastic and deterministic trends if possible. There are two
kinds of statistical tests: one group is based on the unit root
hypothesis while the other is on the stationary null hypothesis.
, that is on the presence of unit roots.
It is important to have techniques available to determine the
actual form of nonstationarity and to distinguish between
stochastic and deterministic trends if possible. There are two
kinds of statistical tests: one group is based on the unit root
hypothesis while the other is on the stationary null hypothesis.
There is a large literature on testing for unit roots theory. A
good survey may be found in Dickey and Bell and Miller (1986), among
others. Let us consider the simple ![]() model:
model:
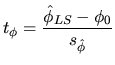
The ![]() model (4.23) can be written as follows by
substracting
model (4.23) can be written as follows by
substracting ![]() to both sides of the equation:
to both sides of the equation:
Up to now it has been shown how to test the null hypothesis of a random
walk (one unit root) against the alternative of a zero mean, stationary
![]() . For economic time series, it could be of interest to consider
alternative hypothesis including stationarity around a constant and/or a
linear trend. This could be achieved by introducing these terms in
model (4.24):
. For economic time series, it could be of interest to consider
alternative hypothesis including stationarity around a constant and/or a
linear trend. This could be achieved by introducing these terms in
model (4.24):
The unit-root null hypothesis is simply
![]() in both
models (4.25)-(4.26). Dickey-Fuller tabulated the
critical values for the corresponding statistics, denoted by
in both
models (4.25)-(4.26). Dickey-Fuller tabulated the
critical values for the corresponding statistics, denoted by
![]() and
and
![]() respectively. It should be noted that
model (4.26) under the null hypothesis becomes a random walk
plus drift model, which is a hypothesis that frequently arises in economic
applications.
respectively. It should be noted that
model (4.26) under the null hypothesis becomes a random walk
plus drift model, which is a hypothesis that frequently arises in economic
applications.
The tests presented so far have the disadvantage that they assume
that the three models considered (4.24), (4.25)
and (4.26) cover all the possibilities under the null
hypothesis. However, many ![]() series do not behave in that way.
In particular, their Data Generating Process may include nuisance
parameters, like an autocorrelated process for the error term, for
example. One method to allow a more flexible dynamic behavior in
the series of interest is to consider that the series
series do not behave in that way.
In particular, their Data Generating Process may include nuisance
parameters, like an autocorrelated process for the error term, for
example. One method to allow a more flexible dynamic behavior in
the series of interest is to consider that the series ![]() follows
an
follows
an ![]() model:
model:
This assumption is not particularly restrictive since every ![]() model always have an
model always have an ![]() representation if its moving average
polynomial is invertible. The
representation if its moving average
polynomial is invertible. The ![]() model can be rewritten as
the following regression model:
model can be rewritten as
the following regression model:
The most common values for ![]() are zero and 1 in economic and business time
series. That is why we have concentrated so far in testing the null
hypothesis of one unit root against the alternative of stationarity
(possibly in deviations from a mean or a linear trend). But it is possible
that the series present more than one unit root. If we want to test, in
general, the hypothesis that a series is
are zero and 1 in economic and business time
series. That is why we have concentrated so far in testing the null
hypothesis of one unit root against the alternative of stationarity
(possibly in deviations from a mean or a linear trend). But it is possible
that the series present more than one unit root. If we want to test, in
general, the hypothesis that a series is ![]() against the alternative
that it is
against the alternative
that it is ![]() , Dickey and Pantula (1987) suggest to follow a sequential
procedure. First, we should test the null hypothesis of
, Dickey and Pantula (1987) suggest to follow a sequential
procedure. First, we should test the null hypothesis of ![]() unit roots
against the alternative of
unit roots
against the alternative of ![]() unit roots. If we reject this
unit roots. If we reject this ![]() ,
then the null hypothesis of
,
then the null hypothesis of ![]() unit roots should be tested against the
alternative of
unit roots should be tested against the
alternative of ![]() unit roots. Last, the null of one unit root is
tested against the alternative of stationarity.
unit roots. Last, the null of one unit root is
tested against the alternative of stationarity.
If we want to check the stationarity of a time series or a linear combination of time series, it would be interesting to test the null hypothesis of stationarity directly. Bearing in mind that the classical hypothesis testing methodology ensures that the null hypothesis is accepted unless there is strong evidence against it, it is not surprising that a good number of empirical work show that standard unit-root tests fail to reject the null hypothesis for many economic time series. Therefore, in trying to decide wether economic data are stationary or integrated, it would be useful to perform tests of the null hypothesis of stationarity as well as tests of the unit-root null hypothesis.
Kwiatkowski, Phillips, Schmidt and Shin (1992) (KPSS) have developed a test for the null hypothesis of stationarity against the alternative of unit root. Let us consider the following Data Generating Process:
Let
![]() , be the LS residuals
of the auxiliary regression:
, be the LS residuals
of the auxiliary regression:
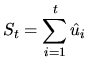
The test statistic developed by KPSS is based on the idea that for
a trend stationary process, the variance of the sum series ![]() should be relative small, while it should be important in the
presence of one unit root. Then, the test statistic for the null
hypothesis of trend stationarity versus a stochastic trend
representation is:
should be relative small, while it should be important in the
presence of one unit root. Then, the test statistic for the null
hypothesis of trend stationarity versus a stochastic trend
representation is:
where
![]() stands for a consistent estimation of the
'long-term' variance of the error term
stands for a consistent estimation of the
'long-term' variance of the error term ![]() . KPSS derived the
asymptotic distribution of this test statistic under the stronger
assumptions that
. KPSS derived the
asymptotic distribution of this test statistic under the stronger
assumptions that ![]() is normal and
is normal and
![]() , and tabulated the corresponding critical values.
Since
, and tabulated the corresponding critical values.
Since ![]() only takes positive values,
this test procedure is an upper tail test. The null hypothesis of trend
stationarity is rejected when
only takes positive values,
this test procedure is an upper tail test. The null hypothesis of trend
stationarity is rejected when ![]() exceeds the critical value.
exceeds the critical value.
The distribution of this test statistic has been tabulated as well for the
special case in which the slope parameter of model (4.30) is ![]() . In such a case, the process
. In such a case, the process ![]() is stationary around a level
(
is stationary around a level
(![]() ) rather than around a trend under the null hypothesis.
Therefore, the residual
) rather than around a trend under the null hypothesis.
Therefore, the residual ![]() , is obtained from the auxiliary
regression of
, is obtained from the auxiliary
regression of ![]() on an intercept only, that is
on an intercept only, that is
![]() .
.
[1,] Order Test Statistic Crit. Value [2,] 0.1 0.05 0.01 [3,] _______________________________________________________ [4,] 2 const 0.105 0.347 0.463 0.739 [5,] 2 trend 0.103 0.119 0.146 0.216