4.4 Forecasting with ARIMA Models

4.4.1 The Optimal Forecast

Let us assume that the series $y_1, y_2, \ldots, y_T$ follows the general $ARIMA(p,d,q)$ model that can be rewritten in terms of the present and past values of $\varepsilon_t$:

$$y_t = \frac{ \Theta(L)}{\Phi(L) \Delta^d} \, \varepsilon_t = \psi... ...fty}(L) \, \varepsilon_t = (1 + \psi_1 L + \psi_2 L^2 +\ldots) \, \varepsilon_t$$ (4.32)

Our objective is to forecast a future value $y_{T+\ell}$ given our information set that consists of the past values $Y_T = (y_T, y_{T-1}, \ldots)$. The future value $y_{T+\ell}$ is generated by model (4.32), thus

$$y_{T+\ell} = \varepsilon_{T+\ell} + \psi_1 \varepsilon_{T+\ell-1} + \psi_2 \varepsilon_{T+\ell-2} + \ldots$$

Let us denote by $y_T(\ell)$ the $\ell$-step ahead forecast of $y_{T+\ell}$ made at origin $T$. It can be shown that, under reasonable weak conditions, the optimal forecast of $y_{T+\ell}$ is the conditional expectation of $y_{T+\ell}$ given the information set, denoted by $E[y_{T+\ell}\vert Y_T]$. The term optimal is used in the sense that minimizes the Mean Squared Error (MSE). Although the conditional expectation does not have to be a linear function of the present and past values of $y_t$, we shall consider linear forecasts because they are fairly easy to work with. Furthermore, if the process is normal, the Minimum MSE forecast (MMSE) is linear. Therefore, the optimal forecast $\ell$-step ahead is:

$$y_T(\ell) = E[y_{T+\ell}\vert Y_T] = E[\varepsilon_{T+\ell}+ \psi_1 \varepsilon_{T+\ell-1} + \psi_2 \varepsilon_{T+\ell-2} + \ldots\vert Y_T]$$

$$= \psi_{\ell} \varepsilon_T + \psi_{\ell+1} \varepsilon_{T-1} + \psi_{\ell+2} \varepsilon_{T-2} + \ldots$$

since past values of $\varepsilon_{T+j}$, for $j \leq0$, are known and future values of $\varepsilon_{T+j}$, for $j > 0$, have zero expectation.

The $\ell$-step ahead forecast error is a linear combination of the future shocks entering the system after time $T$:

$$e_T(\ell) = y_{T+\ell} - y_T(\ell) = \varepsilon_{T+\ell} + \psi_1 \varepsilon_{T+\ell-1} + \ldots + \psi_{\ell-1} \varepsilon_{T+1}$$

Since $E[e_T(\ell)\vert Y_T] = 0$, the forecast $y_T(\ell)$ is unbiased with MSE:

$$MSE[y_T(\ell)] = V(e_T(\ell)) = \sigma^2_{\varepsilon} (1 + \psi_1^2 + \ldots + \psi_{\ell}^2)$$ (4.33)

Given these results, if the process is normal, the $(1-\alpha)$ forecast interval is:

$$\left[\; y_T(\ell) \pm N_{\alpha/2} \sqrt{V(e_T(\ell))}\; \right]$$ (4.34)

For $\ell = 1$, the one-step ahead forecast error is $e_T(1) = y_{T+1} - y_T(1) = \varepsilon_{T+1}$, therefore $\sigma^2_{\varepsilon}$ can be interpreted as the one-step ahead prediction error variance.

4.4.2 Computation of Forecasts

Let us consider again the general $ARIMA(p,d,q)$ model that can be written as well as:

$$\Pi_{p+d}(L) y_t = (1 - \pi_1 L - \pi_2 L^2 - \ldots - \pi_{p+d} L^{p+d}) y_t = \Theta(L) \varepsilon_{t}$$ (4.35)

where $\Pi_{p+d}(L) = \Phi_p(L) (1 - L)^d$. Thus, the future value of $y_{T+\ell}$ generated by (4.35) is:

$$y_{T+\ell} = \pi_1 y_{T+\ell-1} + \ldots + \pi_{p+d} y_{T+\ell-p-... ...} + \theta_1 \varepsilon_{T+\ell-1} + \ldots + \theta_q \varepsilon_{T+\ell-q}$$

and the MMSE forecast is given by the expectation conditional to the information set:

$$y_T(\ell) = \textrm{E}\,[\;y_{T+\ell}\vert Y_T] = \pi_1 E[y_{T+\ell-1}\vert Y_T] + \ldots + \pi_{p+d} E[y_{T+\ell-p-d}\vert Y_T]$$

$$+ E[\varepsilon_{T+\ell}\vert Y_T] + \theta_1 E[\varepsilon_{T+\ell-1}\vert Y_T] + \ldots + \theta_q E[\varepsilon_{T+\ell-q}\vert Y_T]$$

The forecast $y_T(\ell)$ is computed substituting past expectations for known values and future expectations by forecast values, that is:

$$E[y_{T+j}\vert Y_T] = \left\{ \begin{array}{ll} y_{T+j} & j \leq 0 \\ y_T(j) & j > 0 \end{array} \right.$$

$$E[\varepsilon_{T+j}\vert Y_T] = \left\{ \begin{array}{rl} \varepsilon_{T+j} & j \leq 0 \\ 0 & j > 0 \end{array} \right.$$

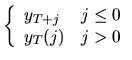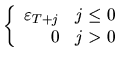In practice, the parameters of the $ARIMA(p,d,q)$ model should be estimated, but for convenience, we assume that they are given.

4.4.3 Eventual Forecast Functions

Following the results of section 4.4.2, if the series $y_t$ follows an $ARIMA(p,d,q)$ model, the $\ell$-step ahead forecast at origin $T$ is given by:

$$y_T(\ell) = \pi_1 y_{T}(\ell-1) + \ldots + \pi_{p+d}\, y_{T}(\ell... ...+ \theta_1 \varepsilon_{T}(\ell-1) + \ldots + \theta_q \varepsilon_{T}(\ell-q)$$

Therefore, when the forecast horizon $\ell > q$:

$$y_T(\ell) = \pi_1 \,y_{T}(\ell-1) + \pi_2\, y_{T}(\ell-2) + \ldots + \pi_{p+d} \, y_{T}(\ell-p-d)$$

That is, the $\ell$-step ahead forecast for $\ell > q$ satisfies the homogeneous difference equation of order $(p+d)$:

$$y_T(\ell) - \pi_1 \,y_{T}(\ell-1) - \pi_2\, y_{T}(\ell-2) - \ldots - \pi_{p+d} \, y_{T}(\ell-p-d) = 0$$ (4.36)

Let us factorize the polynomial $\Pi(L)$ in terms of its roots as follows:

$$\Pi(L) = (1 - \pi_1 L - \pi_2 L^2 - \ldots - \pi_{p+d} L^{p+d}) = \prod_{i=1}^{N} (1 - R_i^{-1} L)^{n_i}$$

where $\sum_{1}^{N} n_i = p+d$. Then, the general solution of the homogeneous difference equation (4.36) is:

$$y_T(\ell) = \sum_{i=1}^{N} \left[ \sum_{j=0}^{n_i-1} k_{ij}^{T} \, \ell^j \right] (R^{-1}_i)^{\ell} \hskip 1cm \ell > q-p-d$$ (4.37)

where $k_{ij}^{T}$ are constants that depend on time origin $T$, that is, these constants change when the forecast origin is changed.

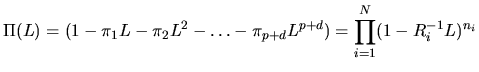
The expression (4.37) is called the eventual forecast function, because it holds only for $\ell > q-p-d$. If $q < p+d$, then the eventual forecast function holds for all $\ell >0$. This eventual forecast function passes through the $(p+d)$ values given by $y_T(q), y_T(q-1), \ldots, y_T(q-p-d+1)$.

4.4.3.0.1 Example 1: Stationary processes.

Let us consider the $ARIMA(1,0,1)$ process in deviations to the mean $\mu$:

$$(1 - \phi L) (y_t - \mu) = (1 + \theta L) \varepsilon_t \qquad \vert\phi\vert<1$$

For $\ell > q=1$, the forecast function $y_T(\ell)$ satisfies the difference equation:

$$(1 - \phi L) (y_t - \mu) = 0$$

Therefore, the eventual forecast function is given by:

$$y_T(\ell) - \mu = k^{T} \phi^{\ell}$$

$$y_T(\ell) = \mu + k^{T} \phi^{\ell} \hskip 1cm \ell > q-p-d = 0$$

Figure 4.12: Forecast of $AR(1)$ model

XEGutsm09.xpl

Let us take as an example the forecast of an $AR(1)$ process with $\delta=0.9$ and $\phi=0.7$. Figure 4.12 shows the eventual forecast function of the model considered (dotted line). It can be observed that this function increases at the beginning until it reaches the mean value, 3. This result, that is,

$$\lim_{\ell \rightarrow \infty} y_T(\ell) = \mu$$

holds for every stationary process. The dashed lines give the interval forecasts, whose limits approach to horizontal parallel lines. This is due to the fact that for every stationary process the $\lim_{\ell \rightarrow \infty} V(e_T(\ell))$ exists and it is equal to $V(y_t)$.

4.4.3.0.2 Example 2: Integrated processes of order 1.

Let us consider the following $ARIMA(0,1,1)$ model:

$$(1 - L) y_t = (1 + \theta L) \varepsilon_t$$

The eventual forecast function is the solution to the difference equation:

$$(1 - L) y_t = 0 \hskip 1cm \ell > q=1$$

that is given by:

$$y_T(\ell) = k^{T} 1^{\ell} = k^{T} \hskip 1cm \ell > q-p-d=0$$

This eventual forecast function passes through the one-step ahead forecast $y_T(1)$ and remains there as $\ell$ increases.

If $\theta =0$, we get the random walk model (4.20) and the eventual forecast function takes the form:

$$y_T(\ell) = y_T \hskip 1cm \ell > 0$$

That is, the optimal forecast is simply the current value, regardless of the forecast horizon. If a shock occurs at time $T$, its effect does not disappear as the forecast horizon increases, because there is no mean to which the process may revert (see graph (a) in figure 4.13).

The eventual forecast function for the random walk plus drift model (4.21) is the solution to the following difference equation:

$$(1 - L) y_t = \delta$$

Thus:

$$y_T(\ell) = k^{T} 1^{\ell} + \delta \ell = k^{T} + \delta \ell$$ (4.38)

Therefore the eventual forecast function is a straight line in which only the intercept depends on the time origin, $T$, through the constant $k^{T}$ (see graph (b) in figure 4.13).

Figure 4.13: Forecast of $I(1)$ models

XEGutsm10.xpl

It can be observed in figure 4.13 that the interval forecast limits increase continuously as the forecast horizon $\ell$ becomes larger. It should be taken into account that when the process is nonstationary the limit $\lim_{\ell \rightarrow \infty} V(e_T(\ell))$ does not exist.

4.4.3.0.3 Example 3: Integrated processes of order 2.

Let us consider the $ARIMA(0,2,2)$ model:

$$(1 - L)^2 y_t = (1 + \theta_1 L + \theta_2 L^2) \varepsilon_t$$

Solving the homogeneous difference equation:     $(1 - L)^2 y_t = 0 \hskip .5cm \ell > 2 \quad$ we get the eventual forecast function as:

$$y_T(\ell) = k_1^{T} 1^{\ell} + k_2^{T} 1^{\ell} \ell = k_1^{T} + k_2^{T} \ell$$

Thus, the eventual forecast function is a straight line passing through the forecasts $y_T(1)$ and $y_T(2)$. Although this forecast function shows the same structure as equation (4.38), it should be noted that both the intercept and the slope of the eventual forecast function depend on the time origin $T$.