4.6 Regression Models for Time Series

In Econometrics the relationships between economic variables proposed by the Economic Theory are usually studied within the framework of linear regression models (see chapters 1 and 2). The data of many economic and business variables are collected in the form of time series. In this section we deal with the problems that may appear when estimating regression models with time series data.

It can be proved that many of the results on the properties of LS estimators and inference rely on the assumption of stationarity of the explanatory variables. Thus, the standard proof of consistency of the LS estimator depends on the assumption plim $ (X'X/T) = Q $, where $ X$ is the data matrix and $ Q$ is a fixed matrix. This assumption implies that the sample moments converge to the population values as the sample size $ T$ increases. But the explanatory variables must be stationary in order to have fixed values in the matrix $ Q$.

As it has been discussed in section 4.3.2, many of the macroeconomic, finance, monetary variables are nonstationary presenting trending behaviour in most cases. From an econometric point view, the presence of a deterministic trend (linear or not) in the explanatory variables does not raise any problem. But many economic and business time series are nonstationary even after eliminating deterministic trends due to the presence of unit roots, that is, they are generated by integrated processes. When nonstationary time series are used in a regression model one may obtain apparently significant relationships from unrelated variables. This phenomenom is called spurious regression. Granger and Newbold (1974) estimated regression models of the type:

$\displaystyle y_t$ $\displaystyle =$ $\displaystyle \beta_0 + \beta_1 x_t + u_t$ (4.54)

where $ y_t $ and $ x_t$ were unrelated random walks:
$\displaystyle \Delta y_t$ $\displaystyle =$ $\displaystyle \varepsilon_{1t} \qquad \varepsilon_{1t} \sim iid(0, \sigma^2_1)$  
$\displaystyle \Delta x_t$ $\displaystyle =$ $\displaystyle \varepsilon_{2t} \qquad \varepsilon_{2t} \sim iid(0, \sigma^2_2)$  

Since $ x_t$ neither affects nor is affected by $ y_t $, one expects the coefficient $ \beta $ to converge to zero and the coefficient of determination, $ R^2$ to also tend to zero. However, they found that, frequently, the null hypothesis of no relationship is not rejected along with very high $ R^2$ and very low Durbin-Watson statistics. It should be noted that the autocorrelation of the random walk $ x_t$ is projected into $ y_t $ which being a random walk as well is also highly correlated. Following these results they suggest that finding high $ R^2$ and low D-W statistics can be a signal of a spurious regression.

These results found by Granger and Newbold (1974) were analytically explained by Phillips (1986). He shows that the t-ratios in model (4.54) do not follow a t-Student distribution and they go to infinity as $ T$ increases. This implies that for any critical value the ratios of rejection of the null hypothesis $ \beta_1=0$ increase with $ T$. Phillips (1986) showed as well that the D-W statistic converges to zero as $ T$ goes to infinity, while it converges to a value different from zero when the variables are related. Then, the value of the D-W statistic may help us to distinguish between genuine and spurious regressions. Summarizing, the spurious regression results are due to the nonstationarity of the variables and the problem is not solved by increasing the sample size $ T$, it even gets worse.

Due to the problems raised by regressing nonstationary variables, econometricians have looked for solutions. One classical approach has been to detrend the series adjusting a determinist trend or including directly a deterministic function of time in the regression model (4.54) to take into account the nonstationary behaviour of the series. However, Phillips (1986) shows that this does not solve the problem if the series are integrated. The t-ratios in the regression model with a deterministic trend do not follow a t-Student distribution and therefore standard inference results could be misleading. Furthermore, it still appears spurious correlation between detrended random walks, that is, spurious regression. A second approach to work with nonstationary series is to look for relationships between stationary differenced series. However, it has to be taken into account that the information about the long-run relationship is lost, and the economic relationship may be different between levels and between increments.


4.6.1 Cointegration

When estimating regression models using time series data it is necessary to know whether the variables are stationary or not (either around a level or a deterministic linear trend) in order to avoid spurious regression problems. This analysis can be perform by using the unit root and stationarity tests presented in section 4.3.3.

It is well known that if two series are integrated to different orders, linear combinations of them will be integrated to the higher of the two orders. Thus, for instance, if two economic variables $ (y_t, x_t)$ are $ I(1)$, the linear combination of them, $ z_t$, will be generally $ I(1)$. But it is possible that certain combinations of those nonstationary series are stationary. Then it is said that the pair $ (y_t, x_t)$ is cointegrated. The notion of cointegration is important to the analysis of long-run relationships between economic time series. Some examples are disposable income and consumption, goverment spending and tax revenues or interest rates on assets of differents maturities. Economic theory suggests that economic time series vectors should move jointly, that is, economic time series should be characterized by means of a long-run equilibrium relationship. Cointegration implies that these pairs of variables have similar stochastic trends. Besides, the dynamics of the economic variables suggests that they may deviate from this equilibrium in the short term, and when the variables are cointegrated the term $ z_t$ is stationary.

The definition of cointegration can be generalized to a set of $ N$ variables (Engle and Granger; 1987): The components of the vector $ y_t $ are said to be co-integrated of order d,b denoted $ y_t \sim CI(d,b)$, if (i) all components of $ y_t $ are $ I(d) $; (ii) there exists a vector $ \alpha (\neq 0)$ so that $ z_t = \alpha'y_t \sim I(d-b), b>0$. The vector $ \alpha $ is called the co-integrating vector.

The relationship $ \alpha'y_t =0$ captures the long-run equilibrium. The term $ \alpha'y_t = z_t$ represents the deviation from the long-run equilibrium so it is called the equilibrium error. In general, more than one cointegrating relationship may exist between $ N$ variables, with a maximum of $ N-1$. For the case of two $ I(1)$ variables, the long-run equilibrium can be written as $ y_{t} = \beta_0 + \beta_1 x_{t}$ and the cointegrating vector is $ (1, - \beta_1$). Clearly the cointegrating vector is not unique, since by multiplying both sides of $ z_t = \alpha'y_t$ by a nonzero scalar the equality remains valid.

4.6.1.0.1 Testing for Cointegration

Engle and Granger (1987) suggest to test whether the vector $ y_t $ is cointegrated by using standard unit-roots statistics such as the $ ADF$ to test the stationarity of the equilibrium error term. For example, in the simple case of two variables $ x_t,y_t \sim I(1)$, to test the null hypothesis of cointegration is equivalent to test the stationarity of $ u_t = y_t - \beta_0 -\beta_1 x_t$. Given that the error term $ u_t$ is not observable, it is approximated by the LS residuals:

$\displaystyle \hat{u}_t = y_t - \hat{\beta}_0 - \hat{\beta}_1 x_t$

and, in order to perform the Dickey-Fuller test, we could estimate the regressions:
$\displaystyle \Delta \hat{u}_t$ $\displaystyle =$ $\displaystyle \alpha + \rho \, \hat{u}_{t-1} + \varepsilon_t$  
$\displaystyle \Delta \hat{u}_t$ $\displaystyle =$ $\displaystyle \alpha + \beta t + \rho \, \hat{u}_{t-1} + \varepsilon_t$  

and examine the corresponding $ \tau_\mu$ or $ \tau_\tau$ statistics. Since the $ ADF$ test is based on estimated values of $ u_t$, the critical values must be corrected. Their asymptotical critical values were computed by Davidson and MacKinnon (1993) (see table 4.6) whereas the critical values for small sample sizes can be found in MacKinnon (1991).


Table 4.6: Asymptotic critical values for the cointegration test
No. Test Significance level
*[1mm] variables statistic 0.01 0.05 0.10
*[1mm] N=2 $ \tau_\mu$ -3.90 -3.34 -3.04
  $ \tau_{\tau} $ -4.32 -3.78 -3.50
N=3 $ \tau_\mu$ -4.29 -3.74 -3.45
  $ \tau_{\tau} $ -4.66 -4.12 -3.84
N=4 $ \tau_\mu$ -4.64 -4.10 -3.81
  $ \tau_{\tau} $ -4.97 -4.43 -4.15
N=5 $ \tau_\mu$ -4.96 -4.42 -4.13
  $ \tau_{\tau} $ -5.25 -4.72 -4.43
N=6 $ \tau_\mu$ -5.25 -4.71 -4.42
  $ \tau_{\tau} $ -5.52 -4.98 -4.70
Source: Davidson and MacKinnon (1993)


4.6.1.0.2 Estimation.

The cointegrating vector $ \alpha $ can be estimated by least squares, that is, by minimizing the sum of the squared deviations from the equilibrium $ z_t$. For example, for a set of two $ I(1)$ variables this criteria is equal to:

$\displaystyle min \sum_{t=1}^{T} (y_{t} - \beta_0 - \beta_1 x_{t})^2$

so, the estimate of the cointegrating vector is calculated by applying least squares on the linear regression:

$\displaystyle y_{t} = \beta_0 + \beta_1 x_{t} + u_t$ (4.55)

which captures the long-run pattern and it is called the co-integrating regression. Given that the variables are cointegrated, the LS estimators have good properties. Stock (1987) proves that this estimator is consistent with a finite sample bias of order $ T^{-1}$ and provides the expression for the asymptotic distribution.

4.6.1.0.3 Example: Consumption and GDP

Let's analyze the relationship between consumption and $ GDP$ in the European Union with quarterly data from 1962 to 2001 (see figure 4.22). The unit root tests conclude that both series are $ I(1)$. The value of the cointegration statistic is -3.79, so both variables are cointegrated. The estimated cointegration relationship is:

$\displaystyle \hat{C}_t = -1.20 + 0.50\, GDP_t $

Figure 4.22: European Union GDP (dotted) and private consumption (solid)
\includegraphics[width=0.8\defpicwidth]{eucoi.ps}


4.6.2 Error Correction Models

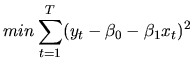
At is has been mentioned above, a classical approach to build regression models for nonstationary variables is to difference the series in order to achieve stationarity and analyze the relationship between stationary variables. Then, the information about the long-run relationship is lost. But the presence of cointegration between regressors and dependent variable implies that the level of these variables are related in the log-run. So, although the variables are nonstationary, it seems more appropriate in this case to estimate the relationship between levels, without differencing the data, that is, to estimate the cointegrating relationship. On the other hand, it could be interesting as well to formulate a model that combines both long-run and short-run behaviour of the variables. This approach is based on the estimation of error correction models ($ ECM$) that relate the change in one variable to the deviations from the long-run equilibrium in the previous period. For example, an $ ECM$ for two $ I(1)$ variables can be written as:

$\displaystyle \Delta y_t = \gamma_0 + \gamma_1(y_{t-1} - \beta_0 - \beta_1 x_{t-1}) + \gamma_2 \Delta x_t + v_t $

The introduction of the equilibrium error of the previous period as explanatory variable in this representation allows us to move towards a new equilibrium, whereas the term $ v_t$ is a stationary disturbance that leads transitory deviations from the equilibrium path. The parameter $ \gamma_1$ measures the speed of the movement towards the new equilibrium.

This model can be generalized as follows (Engle and Granger; 1987): a vector of time series $ y_t $ has an error correction representation if it can be expressed as:

$\displaystyle A(L) (1-L) y_t = -\gamma z_{t-1} + v_t$

where $ v_t$ is a stationary multivariate disturbance, with $ A(0)=I, A(1)$ has all elements finite, $ z_t = \alpha'y_t$ and $ \gamma \neq 0$. The parameters of the correction error form are estimated by substituting the disequilibrium $ z_t$ by the estimate $ \hat{z}_t =\hat{\alpha}^{\prime} y_t$.

In the previous example it means that the following equation is estimated by least squares:

$\displaystyle \Delta y_{t}$ $\displaystyle =$ $\displaystyle \gamma_0 + \gamma_1 \hat{u}_{t-1} + \gamma_2 \Delta x_t + v_t$  

where $ \hat{u}_t$ are the least squares residuals from the cointegrating regression (4.55). The resulting $ \hat{\gamma}$ are consistent and asymptotically normal under standard assumptions.