We show that our treatment of missing values delivers the same results as the procedure
proposed by Shumway and Stoffer (2000,1982). For
this task, let us assume that the
![]() vector of observations
vector of observations ![]()
has missing values. Here, observations 2 and 4 are missing. Thus, we have only ![]() observations. For Kalman filtering in
XploRe
, all missing values in
observations. For Kalman filtering in
XploRe
, all missing values in ![]() and the
corresponding rows and columns in the measurement matrices
and the
corresponding rows and columns in the measurement matrices ![]() ,
, ![]() , and
, and ![]() , are
deleted. Thus, the adjusted vector of observations is
, are
deleted. Thus, the adjusted vector of observations is
where the subscript 1 indicates that this is the vector of observations used in the
XploRe
routines. The procedure of Shumway and Stoffer instead rearranges the
vectors in such a way that the first ![]() entries are the observations--and thus given
by
entries are the observations--and thus given
by ![]() --and the last
--and the last ![]() entries are the missing values. However, all
missing values must be replaced with zeros.
entries are the missing values. However, all
missing values must be replaced with zeros.
For our proof, we use the following generalized formulation of the measurement equation
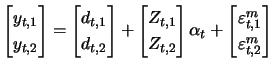 |
and
cov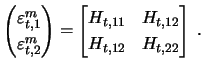 |
![]() contains the observations and
contains the observations and ![]() the missing values. The procedure of
Shumway and Stoffer employs the generalized formulation given above and sets
the missing values. The procedure of
Shumway and Stoffer employs the generalized formulation given above and sets ![]() ,
,
![]() ,
, ![]() , and
, and
![]() (Shumway and Stoffer; 2000, p. 330). We should
remark that the dimensions of these matrices also depend on
(Shumway and Stoffer; 2000, p. 330). We should
remark that the dimensions of these matrices also depend on ![]() via
via ![]() . However, keep notation simple we do not make this time dependency explicit. It is
important to mention that matrices with subscript 1 and 11 are equivalent to the adjusted
matrices of
XploRe
's filtering routines.
. However, keep notation simple we do not make this time dependency explicit. It is
important to mention that matrices with subscript 1 and 11 are equivalent to the adjusted
matrices of
XploRe
's filtering routines.
First, we show by induction that both procedures deliver the same results for the Kalman filter. Once this equivalence is established, we can conclude that the smoother also delivers identical results.
Now, given ![]() and
and ![]() , we have to show that also the filter recursions
, we have to show that also the filter recursions
deliver the same results. Using ss to label the results of the Shumway and Stoffer procedure, we obtain by using
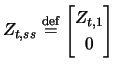 |
that
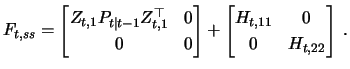 |
The inverse is given by (Sydsæter, Strøm and Berck; 2000, 19.49)
where ![]() is just the covariance matrix of the innovations of
XploRe
's procedure.
With (13.14) we obtain that
is just the covariance matrix of the innovations of
XploRe
's procedure.
With (13.14) we obtain that
and accordingly for the innovations
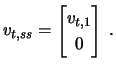 |
We obtain immediately
Plugging this expression into (13.13)--taking into account that
![]() and
and ![]() are identical--delivers
are identical--delivers
| and |
This completes the first part of our proof.
The Kalman smoother recursions use only system matrices that are the same for both
procedures. In addition to the system matrices, the output of the filter is used as an
input, see Subsection 13.5.5. But we have already shown that the filter
output is identical. Thus the results of the smoother are the same for both procedures as
well.
![]()
We want to show that the Kalman smoother produces constant estimates through time for all
state variables that are constant by definition. To proof this result, we use some of the
smoother recursions given in Subsection 13.5.5.
First of all, we rearrange the state vector such that the last
![]() variables
are constant. This allows the following partition of the transition matrix
variables
are constant. This allows the following partition of the transition matrix
with the ![]() identity matrix
identity matrix ![]() . Furthermore, we define with the same partition
. Furthermore, we define with the same partition
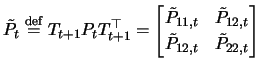 |
The filter recursion for the covariance matrix are given as
where the upper left part of ![]() contains the covariance matrix of the disturbances
for the stochastic state variables. We see immediately that only the upper left part of
contains the covariance matrix of the disturbances
for the stochastic state variables. We see immediately that only the upper left part of
![]() is different from
is different from
![]() .
.
Our goal is to show that for the recursions of the smoother holds
where both ![]() s stand for some complicated matrices. With this result at hand, we obtain
immediately
s stand for some complicated matrices. With this result at hand, we obtain
immediately
| (13.17) |
for all ![]() , where
, where ![]() contains the last
contains the last ![]() elements of the smoothed state
elements of the smoothed state
![]() .
.
Furthermore, it is possible to show with the same result that the lower right partition
of ![]() is equal to the lower right partition of
is equal to the lower right partition of ![]() for all
for all ![]() . This lower right
partition is just the covariance matrix of
. This lower right
partition is just the covariance matrix of ![]() . Just write the smoother recursion
. Just write the smoother recursion
Then check with (13.15) and (13.16) that the lower-right
partition of the first matrix on the right hand side is a ![]() matrix of zeros.
The lower-right partition of the second matrix is given by the the lower-right partition
of
matrix of zeros.
The lower-right partition of the second matrix is given by the the lower-right partition
of ![]() .
.
Now, it is easy to see that
| (13.19) |
We have (Sydsæter, Strøm and Berck; 2000, 19.49)
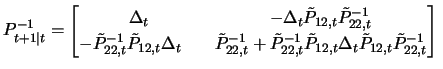 |
(13.20) |
with ![]() as a known function of the partial matrices. If we multiply this matrix
with the lower partition of
as a known function of the partial matrices. If we multiply this matrix
with the lower partition of
![]() we obtain immediately
we obtain immediately ![]() . With this
result and (13.18) we derive (13.16).
. With this
result and (13.18) we derive (13.16).
![]()