13.5 Estimating and filtering in XploRe


13.5.1 Overview

The procedure for Kalman filtering in XploRe is as follows: first, one has to set up the system matrices using 26692 gkalarray . The quantlet adjusts the measurement matrices for missing observations.

After the set up of the system matrices, we calculate the Kalman filter with 26695 gkalfilter . This quantlet also calculates the value of the log likelihood function given in equation (13.9). That value will be used to estimate the unknown parameters of the system matrices with numerical maximization (Hamilton; 1994, Chapter 5). The first and second derivatives of the log likelihood function will also be calculated numerically. To estimate the unknown state vectors--given the estimated parameters--we use the Kalman smoother 26698 gkalsmoother . For diagnostic checking, we use the standardized residuals (13.11). The quantlet 26701 gkalresiduals calculates these residuals.


13.5.2 Setting the system matrices


gkalarrayOut = 26754 gkalarray (Y,M,IM,XM)
sets the system matrices for a time varying SSF

The Kalman filter quantlets need as arguments arrays consisting of the system matrices. The quantlet 26757 gkalarray sets these arrays in a user-friendly way. The routine is especially convenient if one works with time varying system matrices. In our SSF (13.4), only the system matrix $ Z_t$ is time varying. As one can see immediately from the general SSF (13.3), possibly every system matrix can be time varying.

The quantlet uses a three step procedure to set up the system matrices.

  1. To define a system matrix all constant entries must be set to their respective values and all time varying entries must be set to an arbitrary number (for example to 0).
  2. One must define an index matrix for every system matrix. An entry is set to 0 when its corresponding element in the system matrix is constant and to some positive integer when it is not constant.
  3. In addition, for every time varying system matrix, one also has to specify a data matrix that contains the time varying entries.

26760 gkalarray uses the following notation: $ \tt Y$ denotes the matrix of all observations $ [y_1,\hdots, y_T]$, $ \tt M$ denotes the system matrix, $ \tt IM$ denotes the corresponding index matrix and $ \tt XM$ the data matrix.

If all entries of a system matrix are constant over time, then the parameters have already been put directly into the system matrix. In this case, one should set the index and the data matrix to 0.

For every time varying system matrix, only constant parameters--if there are any--have already been specified with the system matrix. The time-varying coefficients have to be specified in the index and the data matrix.

In our example, only the matrices $ Z_t$ are time varying. We have


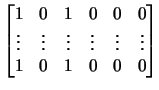$\displaystyle {\tt Z}$ $\displaystyle \stackrel{\mathrm{def}}{=}$ $\displaystyle \begin{bmatrix} 1 & 0 & 1 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & 0 & 1 & 0 & 0 & 0 \end{bmatrix}$  
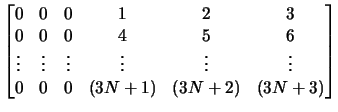$\displaystyle {\tt IZ}$ $\displaystyle \stackrel{\mathrm{def}}{=}$ $\displaystyle \begin{bmatrix} 0 & 0 & 0 & 1 & 2 & 3 \\ 0 & 0 & 0 & 4 & 5 & 6 \... ...\vdots & \vdots & \vdots \\ 0 & 0 & 0 & (3N+1) & (3N+2) & (3N+3) \end{bmatrix}$  
$\displaystyle {\tt XZ}$ $\displaystyle \stackrel{\mathrm{def}}{=}$ $\displaystyle \; {\tt XFGhousequality}$  

The system matrix $ Z_t$ has the dimension $ (N\times6)$. The non-zero entries in the index matrix $ \tt IZ$ prescribe the rows of XFGhousequality , which contain the time varying elements.

The output of the quantlet is an array that stacks the system matrices one after the other. For example, the first two rows of the system matrix $ Z_{41}$ are 

[1,]        1        0        1   6.1048   4.7707       53
[2,]        1        0        1   6.5596   5.1475       13
26775 XFGsssm3.xpl

It is easy to check that the entries in the last three columns are just the characteristics of the first two houses that were sold in 1990:1 (see p. [*]).


13.5.3 Kalman filter and maximized log likelihood


{gkalfilOut,loglike} = 27054 gkalfilter (Y,mu,Sig,ca,Ta,Ra, da,Za,Ha,l)

Kalman filters a time-varying SSF

We assume that the initial state vector at $ t=0$ has mean $ \mu$ and covariance matrix $ \Sigma$. Recall, that $ R_t$ and $ H_t$ denote the covariance matrix of the state noise and--respectively--of the measurement noise. The general filter recursions are as follows:

Start at $ t=1$: use the initial guess for $ \mu$ and $ \Sigma$ to calculate


$\displaystyle a_{1\vert}$ $\displaystyle =$ $\displaystyle c_1 + T_1\mu$  
$\displaystyle P_{1\vert}$ $\displaystyle =$ $\displaystyle T_1\Sigma T_1^\top +R_1$  
$\displaystyle F_1$ $\displaystyle =$ $\displaystyle Z_1 P_{1\vert} Z_1^\top + H_1$  

and


$\displaystyle a_1$ $\displaystyle =$ $\displaystyle a_{1\vert} + P_{1\vert} Z_1^\top F_1^{-1} (y_1 - Z_1 a_{1\vert} - d_1)$  
$\displaystyle P_1$ $\displaystyle =$ $\displaystyle P_{1\vert} - P_{1\vert} Z_1^\top F_1^{-1} Z_1 P_{1\vert}$  

Step at $ t\leqslant T$: using $ a_{t-1}$ and $ P_{t-1}$ from the previous step, calculate


$\displaystyle a_{t\vert t-1}$ $\displaystyle =$ $\displaystyle c_t + T_t a_{t-1}$  
$\displaystyle P_{t\vert t-1}$ $\displaystyle =$ $\displaystyle T_t P_{t-1} T_t^\top + R_t$  
$\displaystyle F_t$ $\displaystyle =$ $\displaystyle Z_t P_{t\vert t-1} Z_t^\top + H_t$  

and


$\displaystyle a_t$ $\displaystyle =$ $\displaystyle a_{t\vert t-1} + P_{t\vert t-1} Z_t^\top F_t^{-1} (y_t - Z_t a_{t\vert t-1} - d_t)$  
$\displaystyle P_t$ $\displaystyle =$ $\displaystyle P_{t\vert t-1} - P_{t\vert t-1} Z_t^\top F_t^{-1} Z_t P_{t\vert t-1}$  

The implementation for our model is as follows: The arguments of 27057 gkalfilter are the data matrix Y, the starting values mu ($ \mu$), Sig ($ \Sigma$) and the array for every system matrix (see section 13.5.2). The output is a $ T+1$ dimensional array of $ [\begin{matrix}a_t & P_t\end{matrix}]$ matrices. If one chooses $ l=1$ the value of the log likelihood function (13.9) is calculated.

Once again, the $ T+1$ matrices are stacked ``behind each other", with the $ t=0$ matrix at the front and the $ t=T$ matrix at the end of the array. The first entry is $ [\begin{matrix}\mu & \Sigma\end{matrix}]$.

How can we provide initial values for the filtering procedure? If the state matrices are non time-varying and the transition matrix $ T$ satisfies some stability condition, we should set the initial values to the unconditional mean and variance of the state vector. $ \Sigma$ is given implicitly by

vec$\displaystyle (\Sigma)=(I-T\otimes T)^{-1}$vec$\displaystyle (R)\;.$    

Here, vec denotes the vec-operator that places the columns of a matrix below each other and $ \otimes$ denotes the Kronecker product. Our model is time-invariant. But does our transition matrix fulfill the stability condition? The necessary and sufficient condition for stability is that the characteristic roots of the transition matrix $ T$ should have modulus less than one (Harvey; 1989, p. 114). It is easy to check that the characteristic roots $ \lambda_j$ of our transition matrix (13.4a) are given as

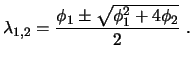$\displaystyle \lambda_{1,2}=\frac{\phi_1\pm\sqrt{\phi_1^2+4\phi_2}}{2}\;.$    

For example, if $ \phi_1$ and $ \phi_2$ are both positive, then $ \phi_1+\phi_2<1$ guarantees real characteristic roots that are smaller than one (Baumol; 1959, p. 221). However, when the AR(2) process of the common price component $ I_t$ has a unit root, the stability conditions are not fulfilled. If we inspect Figure 13.1, a unit root seems quite plausible. Thus we can not use this method to derive the initial values.

If we have some preliminary estimates of $ \mu$, along with preliminary measures of uncertainty--that is a estimate of $ \Sigma$--we can use these preliminary estimates as initial values. A standard way to derive such preliminary estimates is to use OLS. If we have no information at all, we must take diffuse priors about the initial conditions. A method adopted by Koopman, Shephard and Doornik (1999) is setting $ \mu =0$ and $ \Sigma=\kappa I$ where $ \kappa$ is an large number. The large variances on the diagonal of $ \Sigma$ reflect our uncertainty about the true $ \mu$.


Table 13.1: Results for hedonic regression

  coefficient $ t$-statistic $ p$-value
log lot size 0.2675 15.10 0.0000
log floor space 0.4671 23.94 0.0000


age		 -0.0061 -20.84 0.0000
  Regression diagnostics  
$ R^2$ 0.9997 Number of observations 1502
$ \overline{R}^2$ 0.9997 F-statistic 64021.67
$ \hat{\sigma}^2_{\varepsilon}$ 0.4688 Prob(F-statistic) 0.0000


We will use the second approach for providing some preliminary estimates as initial values. Given the hedonic equation (13.1), we use OLS to estimate $ I_t$, $ \beta $, and $ \sigma^2_m$ by regressing log prices on lot size, floor space, age and quarterly time dummies. The estimated coefficients of lot size, floor space and age are reported in Table 13.1. They are highly significant and reasonable in sign and magnitude. Whereas lot size and floor space increase the price on average, age has the opposite effect. According to (13.1), the common price component $ I_t$ is a time-varying constant term and is therefore estimated by the coefficients of the quarterly time dummies, denoted by $ \{\hat{I}_t\}_{t=1}^{80}$. As suggested by (13.2), these estimates are regressed on their lagged values to obtain estimates of the unknown parameters $ \phi_1$, $ \phi_2$, and $ \sigma^2_s$. Table 13.2 presents the results for an AR(2) for the $ \hat{I}_t$ series.


Table 13.2: Time series regression for the quarterly dummies
  coefficient $ t$-statistic $ p$-value
constant 0.5056 1.3350 0.1859
$ \hat{I}_{t-1}$ 0.4643 4.4548 0.0000


$ \hat{I}_{t-2}$		 0.4823 4.6813 0.0000
  Regression diagnostics  
$ R^2$ 0.8780 Number of observations 78
$ \overline{R}^2$ 0.8747 F-statistic 269.81
$ \hat{\sigma}^2_{\nu}$ 0.0063 Prob(F-statistic) 0.0000


The residuals of this regression behave like white noise. We should remark that

$\displaystyle \hat{\phi}_1+\hat{\phi}_2\approx 1$    

and thus the process of the common price component seems to have a unit root.

Given our initial values we maximize the log likelihood (13.9) numerically with respect to the elements of $ \psi^*\stackrel{\mathrm{def}}{=} (\phi_1,\phi_2,\log(\sigma^2_{\nu}),\log(\sigma^2_{\varepsilon})).$ Note that $ \psi^*$ differs from $ \psi $ by using the logarithm of the variances $ \sigma^2_{\nu}$ and $ \sigma^2_{\varepsilon}.$ This transformation is known to improve the numerical stability of the maximization algorithm, which employs 27063 nmBFGS of XploRe 's nummath library. Standard errors are computed from inverting the Hessian matrix provided by 27072 nmhessian . The output of the maximum likelihood estimation procedure is summarized in Table 13.3, where we report the estimates of $ \sigma^2_{\nu}$ and $ \sigma^2_{\varepsilon}$ obtained by retransforming the estimates of $ \log(\sigma^2_{\nu})$ and $ \log(\sigma^2_{\varepsilon})).$


Table: Maximum likelihood estimates of the elements of $ \psi $ 27075 XFGsssm4.xpl
  estimate std error $ t$-value $ p$-value
$ \hat{\psi}_1=$ $ \hat{\phi}_1$ 0.783 0.501 1.56 0.12
$ \hat{\psi}_2=$ $ \hat{\phi}_2$ 0.223 0.504 0.44 0.66
$ \hat{\psi}_1=$ $ \hat{\sigma}^2_{\nu}$ 0.0016 0.012 1.36 0.17
$ \hat{\psi}_2=$ $ \hat{\sigma}^2_{\varepsilon}$ 0.048 0.002 26.7 0
average log likelihood 0.9965    


Note that the maximum likelihood estimates of the AR coefficients $ \phi_1$ and $ \phi_2$ approximately sum to 1, again pointing towards a unit root process for the common price component.


13.5.4 Diagnostic checking with standardized residuals


{V,Vs} = 27360 gkalresiduals (Y,Ta,Ra,da,Za,Ha,gkalfilOut) calculates innovations and standardized residuals

The quantlet gkalresiduals checks internally for the positive definiteness of $ F_t$. An error message will be displayed when $ F_t$ is not positive definite. In such a case, the standardized residuals are not calculated.

The output of the quantlet are two $ N\times T$ matrices V and Vs. V contains the innovations (13.10) and Vs contains the standardized residuals (13.11).

The Q-Q plot of the standardized residuals in Figure 13.2 shows deviations from normality at both tails of the distribution.

Figure 13.2: Deviations of the dotted line from the straight line are evidence for a nonnormal error distribution
\includegraphics[width=1.5\defpicwidth]{XFGsssmdisplay3.ps}

This is evidence, that the true error distribution might be a unimodal distribution with heavier tails than the normal, such as the $ t$-distribution. In this case the projections calculated by the Kalman filter no longer provide the conditional expectations of the state vector but rather its best linear prediction. Moreover the estimates of $ \psi $ calculated from the likelihood (13.9) can be interpreted as pseudo-likelihood estimates.


13.5.5 Calculating the Kalman smoother


gkalsmoothOut = 27483 gkalsmoother (Y,Ta,Ra,gkalfilOut) provides Kalman smoothing of a time-varying SSF

The Kalman filter is a convenient tool for calculating the conditional expectations and covariances of our SSF (13.4). We have used the innovations of this filtering technique and its covariance matrix for calculating the log likelihood. However, for estimating the unknown state vectors, we should use in every step the whole sample information up to period $ T$. For this task, we use the Kalman smoother.

The quantlet 27486 gkalsmoother needs as argument the output of 27489 gkalfilter . The output of the smoother is an array with $ [\begin{matrix}a_{t\vert T} & P_{t\vert T}\end{matrix}]$ matrices. This array of dimension $ T+1$ starts with the $ t=0$ matrix and ends with the matrix for $ t=T$. For the smoother recursions, one needs $ a_t$, $ P_t$ and $ P_{t\vert t-1}$ for $ t=1\dots T$. Then the calculation procedure is as follows:

Start at $ t=T$:


$\displaystyle a_{T\vert T}$ $\displaystyle =$ $\displaystyle a_T$  
$\displaystyle P_{T\vert T}$ $\displaystyle =$ $\displaystyle P_T$  

Step at $ t<T$:

$\displaystyle P^*_{t}$ $\displaystyle =$ $\displaystyle P_{t} T^\top _{t+1} P^{-1}_{t+1\vert t}$  
$\displaystyle a_{t\vert T}$ $\displaystyle =$ $\displaystyle a_{t} + P^*_{t}(a_{t+1\vert T} - T_{t+1} a_{t})$  
$\displaystyle P_{t\vert T}$ $\displaystyle =$ $\displaystyle P_{t} + P^*_{t}(P_{t+1\vert T} - P_{t+1\vert t}) P^{*\top }_{t}$  

The next program calculates the smoothed state vectors for our SSF form, given the estimated parameters $ \tilde{\psi}$. The smoothed series of the common price component is given in Figure 13.3. The confidence intervals are calculated using the variance of the first element of the state vector.

Figure 13.3: Smoothed common price component. Confidence intervals are calculated for the 90% level.
\includegraphics[width=1.5\defpicwidth]{XFGsssmdisplay4.ps}

Comparison with the average prices given in Figure 13.1 reveals that the common price component is less volatile than the simple average. Furthermore, a table for the estimated hedonic coefficients--that is $ \beta $--is generated, Table 13.4.


Table: Estimated hedonic coefficients $ \beta $. 27499 XFGsssm6.xpl
\begin{table}\begin{verbatim}[1,]''===========================================''... ...'' [9,] ''===========================================''\end{verbatim}\end{table}


Recall that these coefficients are just the last three entries in the state vector $ \alpha_t$. According to our state space model, the variances for these state variables are zero. Thus, it is not surprising that the Kalman smoother produces constant estimates through time for these coefficients. In the Appendix 13.6.2 we give a formal proof of this intuitive result.

The estimated coefficient of log lot size implies that, as expected, the size of the lot has an positive influence on the price. The estimated relative price increase for an one percent increase in the lot size is about 0.27%. The estimated effect of an increase in the floor space is even larger. Here, a one percent increase in the floor space lets the price soar by about 0.48%. Finally, note that the price of a houses is estimated to decrease with age.