The goal of density estimation is to
approximate the probability density function
![]() of a random variable
of a random variable ![]() .
Assume we have
.
Assume we have ![]() independent observations
independent observations
![]() from
the random variable
from
the random variable ![]() .
The kernel density estimator
.
The kernel density estimator
![]() for the estimation
of the density value
for the estimation
of the density value ![]() at point
at point ![]() is defined as
is defined as
In order to illustrate how the kernel density estimator works,
let us rewrite equation (6.1) for the Uniform kernel:
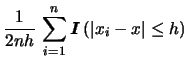 |
|||
![$\displaystyle \frac{1}{2nh}\,
\{\textrm{number of observations } x_i \textrm{ that fall in } [x-h,x+h]\}.
\ $](xlghtmlimg339.gif) |
The Uniform kernel implies that all observations ![]() in the neighborhood of
in the neighborhood of ![]() are given the same weight, since
observations close to
are given the same weight, since
observations close to ![]() carry also information about
carry also information about ![]() .
It is reasonable to attribute more weights to observations
that are near to
.
It is reasonable to attribute more weights to observations
that are near to ![]() and less weight to distant observations. All other kernels
in Table 6.1 have this property. Figure 6.1
visualizes the construction of a kernel density estimate of 10 data points
(
red +
) using the Gaussian kernel.
and less weight to distant observations. All other kernels
in Table 6.1 have this property. Figure 6.1
visualizes the construction of a kernel density estimate of 10 data points
(
red +
) using the Gaussian kernel.
To understand the structure of the
smoother
library, we need to explain
shortly how kernel estimates can be computed in practice.
Consider the equation (6.1) again. To obtain the kernel
density estimates for all observations
![]() we must
compute
we must
compute
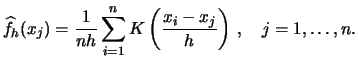
For exploratory purposes, i.e. for graphing the density
estimate it is not necessary to evaluate the
![]() at
all observations
at
all observations
![]() . Instead, the estimate
can be computed for example on an equidistant grid
. Instead, the estimate
can be computed for example on an equidistant grid
![]() :
:
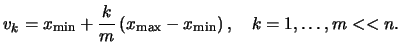
The number of
![]() evaluations of the
kernel function
evaluations of the
kernel function
![]() is however
time consuming if the sample size is large. An alternative
and faster way is to approximate the kernel density estimate
by the WARPing method (Härdle and Scott; 1992).
is however
time consuming if the sample size is large. An alternative
and faster way is to approximate the kernel density estimate
by the WARPing method (Härdle and Scott; 1992).
The basic idea of WARPing (Weighted Average of Rounded Points)
is the ``binning'' of the data in bins of length ![]() starting
at the origin
starting
at the origin ![]() . Each observation point is then replaced by the
bincenter of the corresponding bin (that means in fact that
each point is rounded to the precision given by
. Each observation point is then replaced by the
bincenter of the corresponding bin (that means in fact that
each point is rounded to the precision given by ![]() ). A usual
choice for
). A usual
choice for ![]() is to use
is to use ![]() or
or
![]() .
In the latter case, the effective sample size
.
In the latter case, the effective sample size ![]() for the computation
(the number of nonempty bins) can be at most 101.
for the computation
(the number of nonempty bins) can be at most 101.
For the WARPing method, the kernel function needs to
be evaluated only at
![]() ,
,
![]() , where
, where ![]() is the number of bins which contains the
support of the kernel function.
The calculation of the estimated density reduces then to
is the number of bins which contains the
support of the kernel function.
The calculation of the estimated density reduces then to
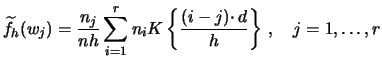
To have a choice between both the exact and the WARPing computation of kernel estimates and related functions, the smoother library offers most functionality in two functions:
| Functionality | Exact | WARPing |
| density estimate |  denxest
denxest |
 denest
denest |
| density confidence intervals |  denxci
denxci |
 denci
denci |
| density confidence bands |  denxcb
denxcb |
 dencb
dencb |
| density bandwidth selection | - |  denbwsel
denbwsel |
The easiest way to compute kernel density estimates is the function
 denest
. This function is based on the WARPing method which
makes the computation very fast.
Let us apply the
denest
. This function is based on the WARPing method which
makes the computation very fast.
Let us apply the
 denest
routine to the
nicfoo
data which contain observations on household netincome in the first
column (see Data Sets (B.1)).
denest
routine to the
nicfoo
data which contain observations on household netincome in the first
column (see Data Sets (B.1)).
 denest
requires the data as a minimum input. Optionally,
the bandwidth h, the kernel function K and the
discretization parameter d which is used for the WARPing can
be specified. For example,
denest
requires the data as a minimum input. Optionally,
the bandwidth h, the kernel function K and the
discretization parameter d which is used for the WARPing can
be specified. For example,
netinc=read("nicfoo")
netinc=netinc[,1]
h=(max(netinc)-min(netinc))*0.15
fh=denest(netinc,h)
To display the estimated function you may use these lines of code:
fh=setmask(fh,"line") plot(fh) tl="Density Estimate" xl="netincome" yl="density fh" setgopt(plotdisplay,1,1,"title",tl,"xlabel",xl,"ylabel",yl)The resulting density is plotted in Figure 6.2.
As an alternative to
 denest
, the function
denest
, the function
 denxest
can be used for obtaining a density estimate by exact computation.
As with
denxest
can be used for obtaining a density estimate by exact computation.
As with
 denest
the data are the minimum input. Optionally,
the bandwidth h, the kernel function K and a grid v
for the computation can be specified. The following code computes
the density estimate for all observations:
denest
the data are the minimum input. Optionally,
the bandwidth h, the kernel function K and a grid v
for the computation can be specified. The following code computes
the density estimate for all observations:
h=(max(netinc)-min(netinc))*0.15 fh=denxest(netinc,h)To compute the density on a grid of 30 equidistant points within the range of x, the previous example can be modified as follows:
h=(max(netinc)-min(netinc))*0.15 v=grid( min(netinc), (max(netinc)-min(netinc))/29, 30) fh=denxest(netinc,h,"qua",v)
Finally, let us calculate the density estimate for a family of different bandwidths in order to see the dependence on the bandwidth parameter. We modify our first code in the following way:
hfac=(max(netinc)-min(netinc)) fh =setmask( denest(netinc,0.15*hfac) ,"line") fh1=setmask( denest(netinc,0.05*hfac) ,"line","thin","magenta") fh2=setmask( denest(netinc,0.10*hfac) ,"line","thin","red") fh3=setmask( denest(netinc,0.20*hfac) ,"line","thin","blue") fh4=setmask( denest(netinc,0.25*hfac) ,"line","thin","green") plot(fh1,fh2,fh3,fh4,fh) tl="Family of Density Estimates" xl="netincome" yl="density fh" setgopt(plotdisplay,1,1,"title",tl,"xlabel",xl,"ylabel",yl)
|
Kernel density estimation requires two parameters: the kernel
function ![]() and the bandwidth parameter
and the bandwidth parameter ![]() . In practice, the choice
of the kernel is not nearly as important as the choice of the kernel.
The theoretical background of this observation is that kernel
functions can be rescaled such that the difference between two kernel
density estimates using two different kernels is almost negligible
(Marron and Nolan; 1988).
. In practice, the choice
of the kernel is not nearly as important as the choice of the kernel.
The theoretical background of this observation is that kernel
functions can be rescaled such that the difference between two kernel
density estimates using two different kernels is almost negligible
(Marron and Nolan; 1988).
Instead of rescaling kernel functions, we can also rescale the bandwidths.
This rescaling works as follows:
Suppose we have estimated an unknown density ![]() using some kernel
using some kernel
![]() and bandwidth
and bandwidth ![]() and we are considering estimating
and we are considering estimating ![]() with
a different kernel, say
with
a different kernel, say ![]() . Then the appropriate bandwidth
. Then the appropriate bandwidth
![]() to use with
to use with ![]() is
is
XploRe
offers the function
 canker
to do this recomputation of
bandwidths:
canker
to do this recomputation of
bandwidths:
hqua=canker(1.0,"gau","qua") hquacomputes the bandwidth
Contents of hqua [1,] 2.6226that can be used with the Quartic kernel "qua" in order to find the kernel density estimate that is equivalent to using the Gaussian kernel "gau" and bandwidth 1.0.
Now we can consider the problem of bandwidth selection. The optimal bandwidth for a kernel density estimate is typically calculated on the basis of an estimate for the integrated squared error
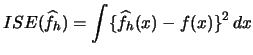
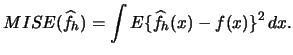
Plug-in approaches attempt to estimate ![]() .
Under the asymptotic conditions
.
Under the asymptotic conditions ![]() and
and
![]() ,
it is possible to approximate
,
it is possible to approximate ![]() by
by
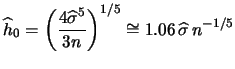
If a different kernel function is used, the bandwidth
![]() can be rescaled by using equation
(6.2). For example, the rule-of-thumb
bandwidth for the Quartic kernel computes as
can be rescaled by using equation
(6.2). For example, the rule-of-thumb
bandwidth for the Quartic kernel computes as
 denrot
.
denrot
.
Of course,
![]() is a very crude estimate, in particular
if the true density
is a very crude estimate, in particular
if the true density ![]() is far from looking like a normal density.
Refined plug-in methods such as the Park and Marron plug-in
and the Sheater and Jones plug-in use nonparametric
estimates for
is far from looking like a normal density.
Refined plug-in methods such as the Park and Marron plug-in
and the Sheater and Jones plug-in use nonparametric
estimates for ![]() .
.
The quantlet
 denbwsel
needs the data vector as input:
denbwsel
needs the data vector as input:
netinc=read("nicfoo")
netinc=netinc[,1]
tmp=denbwsel(netinc)
Choose for instance the Least Squares CV item to use
![]() .
Here, a graphical display appears which shows the
.
Here, a graphical display appears which shows the
![]() criterion
in the upper left, the chosen optimal bandwidth in the upper right,
the resulting kernel density estimate in the lower left, and some
information about the search grid and the kernel in the lower right.
This graphical display is shown in Figure 6.4.
criterion
in the upper left, the chosen optimal bandwidth in the upper right,
the resulting kernel density estimate in the lower left, and some
information about the search grid and the kernel in the lower right.
This graphical display is shown in Figure 6.4.
You can play around now with the different bandwidth selectors. Try out the Park and Marron plug-in for example. Here, in contrast to the cross-validation methods, the aim is to find the root of the bandwidth selection criterion. The graphical display for the Park and Marron selector is shown in Figure 6.5.
During the use of
 denbwsel
, all currently obtained results
are displayed in the output window.
Note that for some selectors, it will be necessary to increase the
search grid for
denbwsel
, all currently obtained results
are displayed in the output window.
Note that for some selectors, it will be necessary to increase the
search grid for ![]() . This can be done by using the menu item
(Change h range or K).
. This can be done by using the menu item
(Change h range or K).
It is difficult to give a general decision of which bandwidth selector
is the best among all. As mentioned above, Silverman's rule of thumb
works well when the true density is approximately normal. It may
oversmooth for bimodal or multimodal densities.
A nice feature of the cross-validation methods is that the selected
bandwidth automatically adapts to the smoothness of ![]() . From a theoretical
point of view, the
. From a theoretical
point of view, the ![]() and
and ![]() bandwidth selectors have the
optimal asymptotic rate of convergence, but need either a very large
sample size or pay with a large variance.
As a consequence, we recommend determining bandwidths by
different selection methods and comparing the resulting
density estimates.
bandwidth selectors have the
optimal asymptotic rate of convergence, but need either a very large
sample size or pay with a large variance.
As a consequence, we recommend determining bandwidths by
different selection methods and comparing the resulting
density estimates.
For detailed overviews on plug-in and cross-validation methods of bandwidth selection, see Härdle (1991), Park and Turlach (1992), and Turlach (1993). Practical experiences are available from the simulation studies in Marron (1989), Jones et al. (1992), Park and Turlach (1992), and Cao et al. (1992).
|
To derive confidence intervals or confidence bands for
![]() one has to know its sampling distribution. The
following result about the asymptotic distribution of
one has to know its sampling distribution. The
following result about the asymptotic distribution of
![]() is known from the literature (Härdle; 1991, p. 62).
Suppose that
is known from the literature (Härdle; 1991, p. 62).
Suppose that ![]() exists and
exists and
![]() . Then
. Then
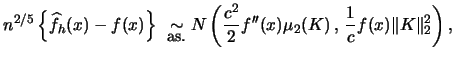 |
(6.7) |
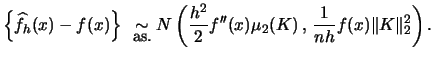 |
(6.8) |
![$\displaystyle \left[\;\widehat{f}_{h}(x)-z_{1-\frac{\alpha}{2}}\sqrt{\frac{\wid...
...alpha}{2}} \sqrt{\frac{\widehat{f}_{h}(x)\Vert K \Vert _{2}^{2}}{nh}}\;\right].$](xlghtmlimg411.gif) |
(6.9) |
The functions
 denci
and
denci
and
 denxci
compute pointwise confidence intervals for a grid
of points (
denxci
compute pointwise confidence intervals for a grid
of points (
 denci
using WARPing) or all
observations (
denci
using WARPing) or all
observations (
 denxci
using exact computation).
The following quantlet code computes the confidence intervals
for bandwidth 0.2 (Gaussian kernel) and significance
level
denxci
using exact computation).
The following quantlet code computes the confidence intervals
for bandwidth 0.2 (Gaussian kernel) and significance
level
![]() . For graphical exploration, the
pointwise intervals are drawn as curves and displayed
in a plot.
The resulting graphics is shown in Figure 6.6.
. For graphical exploration, the
pointwise intervals are drawn as curves and displayed
in a plot.
The resulting graphics is shown in Figure 6.6.
{fh,fl,fu}=denci(netinc,0.2,0.05,"gau")
fh=setmask(fh,"line","blue")
fl=setmask(fl,"line","blue","thin","dashed")
fu=setmask(fu,"line","blue","thin","dashed")
plot(fl,fu,fh)
setgopt(plotdisplay,1,1,"title","Density Confidence Intervals")
Uniform confidence bands for ![]() can only be derived under
some rather restrictive assumptions, see
Härdle (1991, p. 65).
Suppose that
can only be derived under
some rather restrictive assumptions, see
Härdle (1991, p. 65).
Suppose that ![]() is a density on
is a density on ![]() and
and
![]() ,
,
![]() . Then the following formula holds under
some regularity for all
. Then the following formula holds under
some regularity for all
![]() (Bickel and Rosenblatt; 1973):
(Bickel and Rosenblatt; 1973):
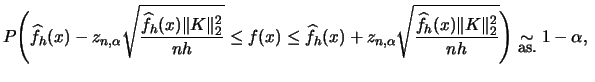 |
(6.10) |
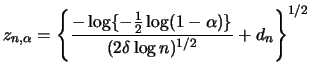
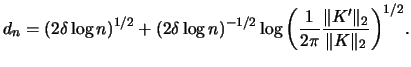
 dencb
and
dencb
and
 denxcb
can hence be
directly applied to the original data
denxcb
can hence be
directly applied to the original data
{fh,fl,fu}=dencb(netinc,0.2,0.05,"gau")
fh=setmask(fh,"line","blue")
fl=setmask(fl,"line","blue","thin","dashed")
fu=setmask(fu,"line","blue","thin","dashed")
plot(fl,fu,fh)
setgopt(plotdisplay,1,1,"title","Density Confidence Bands")
The resulting graph is shown in Figure 6.7.
It can be clearly seen that the confidence bands are wider
than the confidence intervals (Figure 6.6).
This is explained by the fact
that here the whole function
![]() lies within the bands
with probability 95%.
lies within the bands
with probability 95%.