Subsections

• 1.1.1 Integer Arithmetic
• 1.1.2 Floating Point Arithmetic
• 1.1.3 Cancellation
• 1.1.4 Accumulated Roundoff Error
• 1.1.5 Interval Arithmetic

1.1 Computer Arithmetic

Numbers are the lifeblood of statistics, and computational statistics relies heavily on how numbers are represented and manipulated on a computer. Computer hardware and statistical software handle numbers well, and the methodology of computer arithmetic is rarely a concern. However, whenever we push hardware and software to their limits with difficult problems, we can see signs of the mechanics of floating point arithmetic around the frayed edges. To work on difficult problems with confidence and explore the frontiers of statistical methods and software, we need to have a sound understanding of the foundations of computer arithmetic. We need to know how arithmetic works and why things are designed the way they are.

As scientific computation began to rely heavily on computers, a monumental decision was made during the 1960's to change from base ten arithmetic to base two. Humans had been doing base ten arithmetic for only a few hundred years, during which time great advances were possible in science in a short period of time. Consequently, the resistance to this change was strong and understandable. The motivation behind the change to base two arithmetic is merely that it is so very easy to do addition (and subtraction) and multiplication in base two arithmetic. The steps are easy enough that a machine can be designed - wire a board of relays - or design a silicon chip - to do base two arithmetic. Base ten arithmetic is comparatively quite difficult, as its recent mathematical creation would suggest. However two big problems arise in changing from base ten to base two: (1) we need to constantly convert numbers written in base ten by humans to base two number system and then back again to base ten for humans to read the results, and (2) we need to understand the limits of arithmetic in a different number system.

1.1.1 Integer Arithmetic

Computers use two basic ways of writing numbers: fixed point (for integers) and floating point (for real numbers). Numbers are written on a computer following base two positional notation. The positional number system is a convention for expressing a number as a list of integers (digits), representing a number $x$ in base $B$ by a list of digits $a_m,a_{m-1},\ldots,a_1,a_0$ whose mathematical meaning is

$$x = a_{m-1}B^{m-1}+\ldots+a_2B^2+a_1B+a_{0}$$ (1.1)

where the digits $a_j\,$are integers in $\{0,\ldots, B-1\}$. We are accustomed to what is known in the West as the Arabic numbers, $0,1,2,\ldots,9$ representing those digits for writing for humans to read. For base two arithmetic, only two digits are needed $\{0,1\}$. For base sixteen, although often viewed as just a collection of four binary digits ($1$byte$=4$bits), the Arabic numbers are augmented with letters, as $\{0,1,2,\ldots,9,a,b,c,d,e,f \}$, so that $f_{sixteen}=15_{ten}$.

The system based on (1.1), known as fixed point arithmetic, is useful for writing integers. The choice of $m=32$ dominates current computer hardware, although smaller ($m=16$) choices are available via software and larger ($m=48$) hardware had been common in high performance computing. Recent advances in computer architecture may soon lead to the standard changing to $m=64$. While the writing of a number in base two requires only the listing of its binary digits, a convention is necessary for expression of negative numbers. The survivor of many years of intellectual competition is the two's complement convention. Here the first (leftmost) bit is reserved for the sign, using the convention that 0 means positive and 1 means negative. Negative numbers are written by complementing each bit (replace 1 with 0, 0 with 1) and adding one to the result. For $m=16$ (easier to display), this means that $22_{\text{ten}}$ and its negative are written as

$$(0 \; 001 \; 0110) = 22_{\text{ten}}$$

and

$$(1 \; 110 \; 1010) = -22_{\text{ten}}\;.$$

Following the two's complement convention with $m$ bits, the smallest (negative) number that can be written is $-2^{m-1}$ and the largest positive number is $2^{m-1}-1$; zero has a unique representation of ( $\,0\; 000\; \cdots \;0000$). Basic arithmetic (addition and multiplication) using two's complement is easy to code, essentially taking the form of mod $2^{m-1}$ arithmetic, with special tools for overflow and sign changes. See, for example, [8] for history and details, as well as algorithms for base conversions.

The great advantage of fixed point (integer) arithmetic is that it is so very fast. For many applications, integer arithmetic suffices, and most nonscientific computer software only uses fixed point arithmetic. Its second advantage is that it does not suffer from the rounding error inherent in its competitor, floating point arithmetic, whose discussion follows.

1.1.2 Floating Point Arithmetic

To handle a larger subset of the real numbers, the positional notation system includes an exponent to express the location of the radix point (generalization of the decimal point), so that the usual format is a triple (sign, exponent, fraction) to represent a number as

$$x=(-1)^{\text{sign}}B^{\text{exponent}}\left(a_1B^{-1}+a_2B^{-2}+\ldots+a_dB^{-d}\right)\;,$$ (1.2)

where the fraction is expressed by its list of base $B$ digits $0.a_1a_2a_3\ldots a_d$. To preserve as much information as possible with the limited $d$ digits to represent the fraction, normalization is usually enforced, that is, the leading/most significant digit $a_1$ is nonzero - except for the special case $x=0$. The mathematical curiosity of an infinite series expansion of a number has no place here where only $d$ digits are available. Moreover, a critical issue is what to do when only $d$ digits are available. Rounding to the nearest number is preferred to the alternative chopping; in the case of representing $\pi=3.14159265\ldots$ to $d=5$ decimal ($B =$ten) digits leads to the more accurate $(+,+1, 0.31416)$ in the case of rounding, rather than $(+$,$+1$, $0.31415)$ for the chopping alternative. Notice that normalization and the use of this positional notation reflects a goal of preserving relative accuracy, or reducing the relative error in the approximation. The expression of a real number $x$ in floating point arithmetic can be expressed mathematically in terms of a function $fl:R\rightarrow \mathcal{F}$ where $\mathcal{F}$ is the set of numbers that can be represented using this notation, the set of floating point numbers. The relative accuracy of this rounding operation can be expressed as

$$fl(x)=(1+u)x\;,$$ (1.3)

where $\vert u\vert \leq U$ where $U$ is known as the machine unit. Seen in terms of the relative error of $fl(x)$ in approximating $x$, the expression above can be rewritten as

$$\vert x - fl(x) \vert / \vert x \vert \leq U \quad x\neq 0\;.$$

For base $B$ arithmetic with $d$ digits and chopping, $U=B^{1-d}$; rounding reduces $U$ by a factor of $2$.

An important conceptual leap is the understanding that most numbers are represented only approximately in floating point arithmetic. This extends beyond the usual irrational numbers such as $\pi$ or $e$ that cannot be represented with a finite number of digits. A novice user may enter a familiar assignment such as $x=8.6$ and, observing that the computer prints out $8.6000004$, may consider this an error. When the ''$8.6$'' was entered, the computer had to first parse the text ''$8.6$'' and recognize the decimal point and arabic numbers as a representation, for humans, of a real number with the value $8+ 6 \times 10^{-1}$. The second step is to convert this real number to a base two floating point number - approximating this base ten number with the closest base two number - this is the function $fl(\cdot)$. Just as $1/3$ produces the repeating decimal $0.33333\ldots$ in base $10$, the number $8.6$ produces a repeating binary representation $1000.100110011\ldots_{two}$, and is chopped or rounded to the nearest floating point number $fl(8.6)$. Later, in printing this same number out, a second conversion produces the closest base $10$ number to $fl(8.6)$ with few digits; in this case $8.6000004$, not an error at all. Common practice is to employ numbers that are integers divided by powers of two, since they are exactly represented. For example, distributing $1024$ equally spaced points makes more sense than the usual $1000$, since $j/1024$ can be exactly represented for any integer $j$.

A breakthrough in hardware for scientific computing came with the adoption and implementation of the IEEE $754$ binary floating point arithmetic standard, which has standards for two levels of precision, single precision and double precision ([6]). The single precision standard uses $32$ bits to represent a number: a single bit for the sign, $8$ bits for the exponent and $23$ bits for the fraction. The double precision standard requires $64$ bits, using $3$ more bits for the exponent and adds $29$ to the fraction for a total of $52$. Since the leading digit of a normalized number is nonzero, in base two the leading digit must be one. As a result, the floating point form (1.2) above takes a slightly modified form:

$$x=(-1)^{\text{sign}}B^{\text{exponent}-\text{excess}} \left(1+a_1B^{-1}+a_2B^{-2}+\ldots+a_dB^{-d}\right)$$ (1.4)

as the fraction is expressed by its list of binary digits $1.a_1a_2a_3\ldots a_d$. As a result, while only $23$ bits are stored, it works as if one more bit were stored. The exponent using $8$ bits can range from 0 to $255$; however, using an excess of $127$, the range of the difference $({\text{\textit{exponent}}}-{\text{\textit{excess}}})$ goes from $-126$ to $127$. The finite number of bits available for storing numbers means that the set of floating point numbers $\mathcal{F}$ is a finite, discrete set. Although well-ordered, it does have a largest number, smallest number, and smallest positive number. As a result, this IEEE Standard expresses positive numbers from approximately $1.4\times 10^{-45}$ to $3.4\times 10^{38}$ with a machine unit $U=2^{-24}\approx 10^{-7}$ using only $31$ bits. The remaining $32$nd bit is reserved for the sign. Double precision expands the range to roughly $10^{\pm 300}$ with $U=2^{-53}\approx 10^{-16}$, so the number of accurate digits is more than doubled.

The two extreme values of the exponent are employed for special features. At the high end, the case exponent$=255$ signals two infinities ($\pm\infty$) with the largest possible fraction. These values arise as the result of an overflow operation. The most common causes are adding or multiplying two very large numbers, or from a function call that produces a result that is larger than any floating point number. For example, the value of $\exp(x)$ is larger than any finite number in $\mathcal{F}$ for $x>88.73$ in single precision. Before adoption of the standard, $\exp(89.9)$ would cause the program to cease operation due to this ''exception''. Including $\pm\infty$ as members of $\mathcal{F}$ permits the computations to continue, since a sensible result is now available. As a result, further computations involving the value $\pm\infty$ can proceed naturally, such as $1/\infty=0$. Again using the ${\text{exponent}} = 255$, but with any other fraction represents not-a-number, usually written as ''NaN'', and used to express the result of invalid operations, such as $0/0$, $\infty-\infty$, $0\times\infty$, and square roots of negative numbers. For statistical purposes, another important use of NaN is to designate missing values in data. The use of infinities and NaN permit continued execution in the case of anomalous arithmetic operations, instead of causing computation to cease when such anomalies occur. The other extreme ${\text{exponent}} =0$ signals a denormalized number with the net exponent of $-126$ and an unnormalized fraction, with the representation following (1.2), rather than the usual (1.4) with the unstated and unstored 1. The denormalized numbers further expand the available numbers in $\mathcal{F}$, and permit a soft underflow. Underflow, in contrast to overflow, arises when the result of an arithmetic operation is smaller in magnitude than the smallest representable positive number, usually caused by multiplying two small numbers together. These denormalized numbers begin approximately $10^{-38}$ near the reciprocal of the largest positive number. The denormalized numbers provide even smaller numbers, down to $10^{-45}$. Below that, the next number in $\mathcal{F}$ is the floating point zero: the smallest exponent and zero fraction - all bits zero.

Most statistical software employs only double precision arithmetic, and some users become familiar with apparent aberrant behavior such as a sum of residuals of $10^{-16}$ instead of zero. While many areas of science function quite well using single precision, some problems, especially nonlinear optimization, nevertheless require double precision. The use of single precision requires a sound understand of rounding error. However, the same rounding effects remain in double precision, but because their effects are so often obscured from view, double precision may promote a naive view that computers are perfectly accurate.

The machine unit expresses a relative accuracy in storing a real number as a floating point number. Another similar quantity, the machine epsilon, denoted by $\epsilon_m$, is defined as the smallest positive number than, when added to one, gives a result that is different from one. Mathematically, this can be written as

$$fl(1+x)=1\, \,0<x<\epsilon_m\;.$$ (1.5)

Due to the limited precision in floating point arithmetic, adding a number that is much smaller in magnitude than the machine epsilon will not change the result. For example, in single precision, the closest floating point number to $1+2^{-26}$ is 1. Typically, both the machine unit and machine epsilon are nearly the same size, and these terms often used interchangeably without grave consequences.

1.1.3 Cancellation

Often one of the more surprising aspects of floating point arithmetic is that some of the more familiar laws of algebra are occasionally violated: in particular, the associative and distributive laws. While most occurrences are just disconcerting to those unfamiliar to computer arithmetic, one serious concern is cancellation. For a simple example, consider the case of base ten arithmetic with $d=6$ digits, and take $x=123.456$ and $y=123.332$, and note that both $x$ and $y$ may have been rounded, perhaps $x$ was $123.456478$ or $123.456000$ or $123.455998$. Now $x$ would be stored as $(+,3,{.123456})$ and $y$ would be written as $(+,3,{.123332})$, and when these two numbers are subtracted, we have the unnormalized difference $(+,3,{.000124})$. Normalization would lead to $(+,0,{.124\text{???}})$ where merely ''?'' represents that some digits need to take their place. The simplistic option is to put zeros, but ${.124478}$ is just as good an estimate of the true difference between $x$ and $y$ as ${.124000}$, or ${.123998}$, for that matter. The problem with cancellation is that the relative accuracy that floating point arithmetic aims to protect has been corrupted by the loss of the leading significant digits. Instead of a small error in the sixth digit, we now have that error in the third digit; the relative error has effectively been magnified by a factor of $1000$ due to the cancellation of the first $3$ digits.

The best way to deal with the potential problem caused by catastrophic cancellation is to avoid them. In many cases, the cancellation may be avoided by reworking the computations analytically to handle the cancellation:

$$1-(1-2t)^{-1}=\frac{1-2t-1}{1-2t}=\frac{-2t}{1-2t}\;.$$

In this case, there is significant cancellation when $t$ is small, and catastrophic cancellation whenever $t$ drops below the machine epsilon. Using six digit decimal arithmetic to illustrate, at $t=0.001$, the left hand expression, $1-(1-2t)^{-1}$, gives

$$1.00000-1.00200={.200000}\times 10^{-2}$$

while the right hand expression, $-2t/(1-2t)$, gives

$${.200401}\times 10^{-2}\;.$$

The relative error in using the left hand expression is an unacceptable ${.002}$. At $t=10^{-7}$, the first expression leads to a complete cancellation yielding zero and a relative error of one. Just a little algebra here avoids the most of the effect of cancellation. When the expressions involve functions, cases where cancellation occurs can often be handled by approximations. In the case of $1-\mathrm{e}^{-t}$, serious cancellation will occur whenever $t$ is very small. The cancellation can be avoided for this case by using a power series expansion:

$$1-\mathrm{e}^{-t}=1-\left(1-t+t^2/2-\ldots\right)\approx t-t^2/2=t\left(1-t/2\right)\;.$$

When $t={.0001}$, the expression $1-\mathrm{e}^{-t}$ leads to the steps

$$1.00000-0.999900={.100000}\times 10^{-4}\;,$$

while the approximation gives

$$({.0001})({.999950})={.999950}\times 10^{-4}$$

which properly approximates the result to six decimal digits. At $t=10^{-5}$ and $10^{-6}$, similar results occur, with complete cancellation at $10^{-7}$. Often the approximation will be accurate just when cancellation must be avoided.

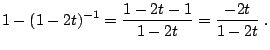One application where rounding error must be understood and cancellation cannot be avoided is numerical differentiation, where calls to a function are used to approximate a derivative from a first difference:

$$f^{\prime}(x)\approx\left[\,f(x+h)-f(x)\right]/h\;.$$ (1.6)

Mathematically, the accuracy of this approximation is improved by taking $h$ very small; following a quadratic Taylor's approximation, we can estimate the error as

$$\left[\,f(x+h)-f(x)\right]/h\approx f'(x)+\frac{1}{2}hf''(x)\;.$$

However, when the function calls $f(x)$ and $f(x+h)$ are available only to limited precision - a relative error of $\epsilon_m$, taking $h$ smaller leads to more cancellation. The cancellation appears as a random rounding error in the numerator of (1.6) which becomes magnified by dividing by a small $h$. Taking $h$ larger incurs more bias from the approximation; taking $h$ smaller incurs larger variance from the rounding error. Prudence dictates balancing bias and variance. [3] recommend using $h\approx\epsilon_m^{1/2}$ for first differences, but see also [1].

The second approach for avoiding the effects of cancellation is to develop different methods. A common cancellation problem in statistics arises from using the formula

$$\sum_{i=1}^ny^2_i-n\overline{y}^2$$ (1.7)

for computing the sum of squares around the mean. Cancellation can be avoided by following the more familiar two-pass method

$$\sum_{i=1}^n(y_i-\overline{y})^2$$ (1.8)

but this algorithm requires all of the observations to be stored and repeated updates are difficult. A simple adjustment to avoid cancellation, requiring only a single pass and little storage, uses the first observation to center:

$$\sum_{i=1}^{n}(y_{i} - \overline{y})^{2} = \sum_{i=1}^{n}(y_{i} - y_{1})^{2} - n(y_{1} - \overline{y})^{2}\;.$$ (1.9)

An orthogonalization method from regression using Givens rotations (see [2]) can do even better:

$$t_{i} = t_{i-1} + y_{i}$$ (1.10)

$$s_{i} = s_{i-1} + (iy_{i} - t_{i})^{2}/(i(i - 1))\;.$$ (1.11)

To illustrate the effect of cancellation, take the simple problem of $n = 5$ observations, $y_{i} = 4152 + i$ so that $y_{1} = 4153$ through $y_{5} = 4157$. Again using six decimal digits, the computations of the sum and mean encounter no problems, and we easily get $\overline{y} = 4155$ or ${.415500} \times 10^{4}$, and $\sum y_{i} = 20775$ or ${.207750} \times 10^{5}$. However, each square loses some precision in rounding:

$$y_1=4153\;, \quad y^2_1 = 4153^2 = {17{,}247{,}409} \quad{.172474} \times 10^8$$

$$y_2=4154\;, \quad y^2_2 = 4154^2 = {17{,}255{,}716} \quad{.172557} \times 10^8$$

$$y_3=4155\;, \quad y^2_3 = 4155^2 = {17{,}264{,}025} \quad{.172640} \times 10^8$$

$$y_4=4156\;, \quad y^2_4 = 4156^2 = {17{,}272{,}336} \quad{.172723} \times 10^8$$

$$y_5=4157\;, \quad y^2_5 = 4157^2 = {17{,}280{,}649} \quad{.172806} \times 10^8\;.$$

Summing the squares encounters no further rounding on its way to $0.863200\times 10^8$, and we compute the corrected sum of squares as

$${.863200} \times 10^8-({.207750}\times 10^5) \times 4155$$

$${.863200} \times 10^8-{.863201} \times 10^8=-100\;.$$

The other three algorithms, following (1.8), (1.9), (1.10), and (1.11), each give the perfect result of $28$ in this case.

Admittedly, while this example is contrived to show an absurd result, a negative sum of squares, the equally absurd value of zero is hardly unusual. Similar computations - differences of sum of squares - are routine, especially in regression and in the computation of eigenvalues and eigenvectors. In regression, the orthogonalization method (1.10) and (1.11) is more commonly seen in its general form. In all these cases, simply centering can improve the computational difficulty and reduce the effect of limited precision arithmetic.

1.1.4 Accumulated Roundoff Error

Another problem with floating point arithmetic is the sheer accumulation of rounding error. While many applications run well in spite of a large number of calculations, some approaches encounter surprising problems. An enlightening example is just to add up many ones: $1+1+1+\ldots$. Astonishingly, this infinite series appears to converge - the partial sums stop increasing as soon as the ratio of the new number to be added, in this case, one, to the current sum ($n$) drops below the machine epsilon. Following (1.5), we have $fl(n+1)=fl(n)$, from which we find

$$1/n\approx\epsilon_m \quad n\approx 1/\epsilon_m\;.$$

So you will find the infinite series of ones converging to $1/\epsilon_m$. Moving to double precision arithmetic pushes this limit of accuracy sufficiently far to avoid most problems - but it does not eliminate them. A good mnemonic for assessing the effect of accumulated rounding error is that doing $m$ additions amplifies the rounding error by a factor of $m$. For single precision, adding $1000$ numbers would look like a relative error of $10^{-4}$ which is often unacceptable, while moving to double precision would lead to an error of $10^{-13}$. Avoidance strategies, such as adding smallest to largest and nested partial sums, are discussed in detail in Monahan, 2001, Chap. 2.

1.1.5 Interval Arithmetic

One of the more interesting methods for dealing with the inaccuracies of floating point arithmetic is interval arithmetic. The key is that a computer can only do arithmetic operations: addition, subtraction, multiplication, and division. The novel idea, though, is that instead of storing the number $x$, its lower and upper bounds $(\underline{x}, \overline{x})$ are stored, designating an interval for $x$. Bounds for each of these arithmetic operations can be then established as functions of the input. For addition, the relationship can be written as:

$$\underline{x} + \underline{y} < x + y < \overline{x} + \overline{y}\;.$$

Similar bounds for the other three operations can be established. The propagation of rounding error through each step is then captured by successive upper and lower bounds on intermediate quantities. This is especially effective in probability calculations using series or continued fraction expansions. The final result is an interval that we can confidently claim contains the desired calculation. The hope is always that interval is small. Software for performing interval arithmetic has been implemented in a practical fashion by modifying a Fortran compiler. See, for example, [5] for an introductory survey, and [7] for articles on applications.