Subsections

• 1.2.1 Iterative Algorithms
• 1.2.2 Iterative Algorithms for Optimization and Nonlinear Equations

1.2 Algorithms

An algorithm is a list of directed actions to accomplish a designated task. Cooking recipes are the best examples of algorithms in everyday life. The level of a cookbook reflect the skill of the cook: a gourmet cookbook may include the instruction ''saute the onion until transparent'' while a beginner's cookbook would describe how to choose and slice the onion, what kind of pan, the level of heat, etc. Since computers are inanimate objects incapable of thought, instructions for a computer algorithm must go much, much further to be completely clear and unambiguous, and include all details.

Most cooking recipes would be called single pass algorithms, since they are a list of commands to be completed in consecutive order. Repeating the execution of the same tasks, as in baking batches of cookies, would be described in algorithmic terms as looping. Looping is the most common feature in mathematical algorithms, where a specific task, or similar tasks, are to be repeated many times. The computation of an inner product is commonly implemented using a loop:

$$\boldsymbol{a}^{\top} \boldsymbol{b} = a_{1} b_{1} + a_{2} b_{2} + \ldots + a_{n} b_{n}\;,$$

implemented as

$s = 0$

do $i = 1$ to $n$

         $s = s + a_{i} \times b_{i}$

end do

where the range of the loop includes the single statement with a multiplication and addition. In an iterative algorithm, the number of times the loop is be repeated is not known in advance, but determined by some monitoring mechanism. For mathematical algorithms, the focus is most often monitoring convergence of a sequence or series. Care must be taken in implementing iterative algorithms to insure that, at some point, the loop will be terminated, otherwise an improperly coded procedure may proceed indefinitely in an infinite loop. Surprises occur when the convergence of an algorithm can be proven analytically, but, because of the discrete nature of floating point arithmetic, the procedure implementing that algorithm may not converge. For example, in a square-root problem to be examined further momentarily, we cannot find $x\in\mathcal{F}$ so that $x\times x$ is exactly equal to $2$. The square of one number may be just below two, and the square of the next largest number in $\mathcal{F}$ may be larger than $2$. When monitoring convergence, common practice is to convert any test for equality of two floating point numbers or expressions to tests of closeness:

$${\tt if}$$

$$\quad ( (x^{\ast} x - 2 ) < )$$ (1.12)

$${\tt then}\; {\tt exit.}$$

Most mathematical algorithms have more sophisticated features. Some algorithms are recursive, employing relationships such as the gamma function: $\Gamma(x+1)=x\Gamma(x)$ so that new values can be computed using previous values. Powerful recursive algorithms, such as the Fast Fourier Transform (FFT) and sorting algorithms, follow a divide-and-conquer paradigm: to solve a big problem, break it into little problems and use the solutions to the little problems to solve the big problem. In the case of sorting, the algorithm may look something like:

algorithm sort(list)

break list into two pieces: first and second

sort (first)

sort (second)

put sorted lists first and second together to form

        one sorted list

end algorithm sort

Implemented recursively, a big problem is quickly broken into tiny pieces and the key to the performance of divide-and-conquer algorithms is in combining the solutions to lots of little problems to address the big problem. In cases where these solutions can be easily combined, these recursive algorithms can achieve remarkable breakthroughs in performance. In the case of sorting, the standard algorithm, known as bubblesort, takes $O(n^2)$ work to sort a problem of size $n$ - if the size of the problem is doubled, the work goes up by factor of $4$. The Discrete Fourier Transform, when written as the multiplication of an $n \times n$ matrix and a vector, involves $n^2$ multiplications and additions. In both cases, the problem is broken into two subproblems, and the mathematics of divide and conquer follows a simple recursive relationship, that the time/work $T(n)$ to solve a problem of size $n$ is the twice the time/work to solve two subproblem with half the size, plus the time/work $C(n)$, to put the solutions together:

$$T(n)=2T\left(n/2\right)+C(n)\;.$$ (1.13)

In both sorting and the Discrete Fourier Transform, $C(n)\approx cn+d$, which leads to $T(n)=cn\log(n)+O(n)$. A function growing at the rate $O(n\log n)$ grows so much slower than $O(n^2)$, that the moniker ''Fast'' in Fast Fourier Transform is well deserved. While some computer languages preclude the use of recursion, recursive algorithms can often be implemented without explicit recursion through clever programming.

The performance of an algorithm may be measured in many ways, depending on the characteristics of the problems the it may be intended to solve. The sample variance problem above provides an example. The simple algorithm using (1.7) requires minimal storage and computation, but may lose accuracy when the variance is much smaller than the mean: the common test problem for exhibiting catastrophic cancellation employs $y_i=2^{12}+i$ for single precision. The two-pass method (1.8) requires all of the observations to be stored, but provides the most accuracy and least computation. Centering using the first observation (1.9) is nearly as fast, requires no extra storage, and its accuracy only suffers when the first observation is unlike the others. The last method, arising from the use of Givens transformations (1.10) and (1.11), also requires no extra storage, gives sound accuracy, but requires more computation. As commonly seen in the marketplace of ideas, the inferior methods have not survived, and the remaining competitors all have tradeoffs with speed, storage, and numerical stability.

1.2.1 Iterative Algorithms

The most common difficult numerical problems in statistics involve optimization, or root-finding: maximum likelihood, nonlinear least squares, M-estimation, solving the likelihood equations or generalized estimating equations. And the algorithms for solving these problems are typically iterative algorithms, using the results from the current step to direct the next step.

To illustrate, consider the problem of computing the square root of a real number $y$. Following from the previous discussion of floating point arithmetic, we can restrict $y$ to the interval $(1,2)$. One approach is to view the problem as a root-finding problem, that is, we seek $x$ such that $f(x)=x^2-y=0$. The bisection algorithm is a simple, stable method for finding a root. In this case, we may start with an interval known to contain the root, say $(x_1,x_2)$, with $x_1=1$ and $x_2 = 2$. Then bisection tries $x_3 = 1.5$, the midpoint of the current interval. If $f(x_3)<0$, then $x_3<\sqrt{y}<x_2$, and the root is known to belong in the new interval $(x_3,x_2)$. The algorithm continues by testing the midpoint of the current interval, and eliminating half of the interval. The rate of convergence of this algorithm is linear, since the interval of uncertainty, in this case, is cut by a constant $(1/2)$ with each step. For other algorithms, we may measure the rate at which the distance from the root decreases. Adapting Newton's method to this root-finding problem yields Heron's iteration

$$x_{n+1}=\frac{1}{2}(x_n+y/x_n)\;.$$

Denoting the solution as $x^{\ast}=\sqrt{y}$, the error at step $n$ can be defined as $\epsilon_n=x_n-x^{\ast}$, leading to the relationship

$$\epsilon_{n+1}=\frac{1}{2}\frac{\epsilon^2_n}{x_n}\;.$$ (1.14)

This relationship of the errors is usually called quadratic convergence, since the new error is proportional to the square of the error at the previous step. The relative error $\delta_n=(x_n-x^{\ast})/x^{\ast}$ follows a similar relationship,

$$\delta_n=\frac{1}{2}\delta^2_n/(1+\delta_n)\;.$$ (1.15)

Here, the number of accurate digits is doubled with each iteration. For the secant algorithm, analysis of the error often leads to a relationship similar to (1.14), but $\vert\epsilon_{n+1}\vert\approx C\vert\epsilon_n\vert^p$, with $1<p<2$, achieving a rate of convergence known as superlinear. For some well-defined problems, as the square root problem above, the number of iterations needed to reduce the error or relative error below some criterion can be determined in advance.

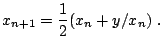While we can stop this algorithm when $f(x_n)=0$, as discussed previously, there may not be any floating point number that will give a zero to the function, hence the stopping rule (1.12). Often in root-finding problems, we stop when $\vert f(x_n)\vert$ is small enough. In some problems, the appropriate ''small enough'' quantity to ensure the desired accuracy may depend on parameters of the problem, as in this case, the value of $y$. As a result, termination criterion for the algorithm is changed to: stop when the relative change in $x$ is small

$$\vert x_{n+1}-x_n\vert/\vert x_n\vert<\delta\;.$$

While this condition may cause premature stopping in rare cases, it will prevent infinite looping in other cases. Many optimization algorithms permit the iteration to be terminated using any combination - and ''small enough'' is within the user's control. Nevertheless, unless the user learns a lot about the nature of the problem at hand, an unrealistic demand for accuracy can lead to unachievable termination criteria, and an endless search.

As discussed previously, rounding error with floating point computation affects the level of accuracy that is possible with iterative algorithms for root-finding. In general, the relative error in the root is at the same relative level as the computation of the function. While optimization problems have many of the same characteristics as root-finding problems, the effect of computational error is a bit more substantial: $k$ digits of accuracy in the function to be optimization can produce but $k/2$ digits in the root/solution.

1.2.2 Iterative Algorithms for Optimization and Nonlinear Equations

In the multidimensional case, the common problems are solving a system of nonlinear equations or optimizing a function of several variables. The most common tools for these problems are Newton's method or secant-like variations. Given the appropriate regularity conditions, again we can achieve quadratic convergence with Newton's method, and superlinear convergence with secant-like variations. In the case of optimization, we seek to minimize $f(x)$, and Newton's method is based on minimizing the quadratic approximation:

$$f(\boldsymbol{x})\approx f (\boldsymbol{x}_0)+(\boldsymbol{x}-\bo... ...p} \boldsymbol{\nabla}^2f(\boldsymbol{x}_0)(\boldsymbol{x}-\boldsymbol{x}_0)\;.$$

This leads to the iteration step

$$\boldsymbol{x}^{(n+1)} = \boldsymbol{x}^{(n)} - \left[ \boldsymbo... ...}\right) \right]^{-1} \boldsymbol{\nabla} f\left(\boldsymbol{x}^{(n)}\right)\;.$$

In the case of solving a system of nonlinear equations, $\boldsymbol{g}(\boldsymbol{x})=\boldsymbol{0}$, Newton's method arises from solving the affine (linear) approximation

$$\boldsymbol{g}(\boldsymbol{x}) \approx \boldsymbol{g}\left(\bolds... ...left(\boldsymbol{x}_{0}\right)\left(\boldsymbol{x}-\boldsymbol{x}_{0}\right)\;,$$

leading to a similar iteration step

$$\boldsymbol{x}^{(n+1)} = \boldsymbol{x}^{(n)}-[ \boldsymbol{J}_{\boldsymbol{g}}(\boldsymbol{x}^{(n)}) ]^{-1}\boldsymbol{g}(\boldsymbol{x}^{(n)})\;.$$

In both cases, under suitable smoothness conditions, the Newton iteration will achieve quadratic convergence - using norms to measure the error at each step:

$$\left \Vert \boldsymbol{x}^{(n+1)}-\boldsymbol{x}^{\ast} \right \... ...prox C \left \Vert \boldsymbol{x}^{(n)}-\boldsymbol{x}^{\ast} \right \Vert^2\;.$$

For both problems, Newton's method requires the computation of lots of derivatives, either the gradient $\boldsymbol{\nabla} f (\boldsymbol{x}_0)$ and Hessian $\boldsymbol{\nabla}^2f (\boldsymbol{x}_0)$, or the Jacobian matrix $\boldsymbol{J}_{\boldsymbol{g}}(\boldsymbol{x}^{(n)})$. In the univariate root-finding problem, the secant method arises by approximating the derivative with the first difference using the previous evaluation of the function. Secant analogues can be constructed for both the optimization and nonlinear equations problems, with similar reduction in the convergence rate: from quadratic to superlinear.

In both problems, the scaling of the parameters is quite important, as measuring the error with the Euclidean norm presupposes that errors in each component are equally weighted. Most software for optimization includes a parameter vector for suitably scaling the parameters, so that one larger parameter does not dominate the convergence decision. In solving nonlinear equations, the condition of the problem is given by

$$\left \Vert \boldsymbol{J}_{\boldsymbol{g}} \left(\boldsymbol{x}^... ...l{J}_{\boldsymbol{g}}\left(\boldsymbol{x}^{(n)}\right)\right]^{-1} \right \Vert$$

(as in solving linear equations) and scaling problem extends to the components of $\boldsymbol{g}(\boldsymbol{x})$. In many statistical problems, such as robust regression, the normal parameter scaling issues arise with the covariates and their coefficients. However, one component of $\boldsymbol{g}(\boldsymbol{x})$, associated with the error scale parameter may be orders of magnitude larger or smaller than the other equations. As with parameter scaling, this is often best done by the user and is not easily overcome automatically.

With the optimization problem, there is a natural scaling with $\boldsymbol{\nabla} f (\boldsymbol{x}_0)$ in contrast with the Jacobian matrix. Here, the eigenvectors of the Hessian matrix $\boldsymbol{\nabla}^2f (\boldsymbol{x}_0)$ dictate the condition of the problem; see, for example, [4] and [3]. Again, parameter scaling remains one of the most important tools.