In this section, some of the most common smoothing methods are introduced and discussed.
The simplest of smoothing methods is a kernel smoother. A point ![]() is fixed in the domain of the mean function
is fixed in the domain of the mean function
![]() , and
a smoothing window is defined around that point. Most often, the
smoothing window is simply an interval
, and
a smoothing window is defined around that point. Most often, the
smoothing window is simply an interval ![]() , where
, where ![]() is
a fixed parameter known as the bandwidth.
is
a fixed parameter known as the bandwidth.
The kernel estimate is a weighted average of the observations within the smoothing window:
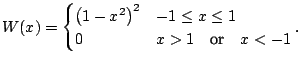 |
The kernel smoother can be represented as
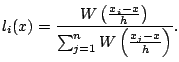 |
The kernel estimate (5.2) is sometimes called the Nadaraya-Watson estimate ([23,33]). Its simplicity makes it easy to understand and implement, and it is available in many statistical software packages. But its simplicity leads to a number of weaknesses, the most obvious of which is boundary bias. This can be illustrated through an example.
![\includegraphics[width=8.0cm]{text/3-5/lrfig1.eps}](img4041.gif)
|
The fuel economy dataset consists of measurements of fuel usage (in
miles per gallon) for sixty different vehicles. The predictor variable
is the weight (in pounds) of the vehicle. Figure 5.1
shows a scatterplot of the sixty data points, together with a kernel
smooth. The smooth is constructed using the bisquare kernel and
bandwidth ![]() pounds.
pounds.
Over much of the domain of Fig. 5.1, the smooth fit
captures the main trend of the data, as required. But consider the
left boundary region; in particular, vehicles weighing less than
![]() pounds. All these data points lie above the fitted
curve; the fitted curve will underestimate the economy of vehicles in
this weight range. When the kernel estimate is applied at the left
boundary (say, at
Weight
pounds. All these data points lie above the fitted
curve; the fitted curve will underestimate the economy of vehicles in
this weight range. When the kernel estimate is applied at the left
boundary (say, at
Weight![]() ), all the data points used to
form the average have
Weight
), all the data points used to
form the average have
Weight![]() , and correspondingly slope
of the true relation induces boundary bias
into the estimate.
, and correspondingly slope
of the true relation induces boundary bias
into the estimate.
More discussion of this and other weaknesses of the kernel smoother can be found in [13]. Many modified kernel estimates have been proposed, but one obtains more parsimonious solutions by considering alternative estimation procedures.
Local regression estimation was independently introduced in several different fields in the late nineteenth and early twentieth century ([15,27]). In the statistical literature, the method was independently introduced from different viewpoints in the late 1970's ([4,18,29]). Books on the topic include [8] and [21].
The underlying principle is that a smooth function can be well
approximated by a low degree polynomial in the neighborhood of any
point ![]() . For example, a local linear approximation is
. For example, a local linear approximation is
The local approximation can be fitted by locally weighted least
squares. A weight function and bandwidth
are defined as for kernel regression. In the case of local linear
regression, coefficient estimates
![]() are chosen to
minimize
are chosen to
minimize
Since (5.5) is a weighted least squares problem, one can obtain the coefficient estimates by solving the normal equations
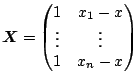 |
When
![]() is invertible, one has the
explicit representation
is invertible, one has the
explicit representation
For local quadratic regression and higher order fits, one simply adds
additional columns to the design matrix
![]() and
vector
and
vector
![]() .
.
Figure 5.2 shows a local linear regression
fit to the fuel economy dataset. This has clearly fixed the boundary
bias problem observed in Fig. 5.1. With the reduction in
boundary bias, it is also possible to substantially increase the
bandwidth, from ![]() pounds to
pounds to ![]() bounds. As a result, the
local linear fit is using much more data, meaning the estimate has
less noise.
bounds. As a result, the
local linear fit is using much more data, meaning the estimate has
less noise.
An entirely different approach to smoothing is through optimization of a penalized least squares criterion, such as
The solution to this optimization problem is a piecewise polynomial, or spline function, and so penalized least squares methods are also known as smoothing splines. The idea was first considered in the early twentieth century ([34]). Modern statistical literature on smoothing splines began with work including [32] and [28]. Books devoted to spline smoothing include [10] and [31].
Suppose the data are ordered;
![]() for all
for all ![]() . Let
. Let
![]() , and
, and
![]() , for
, for
![]() . Given these values, it is easy to show that between
successive data points,
. Given these values, it is easy to show that between
successive data points,
![]() must be the unique cubic
polynomial interpolating these values:
must be the unique cubic
polynomial interpolating these values:
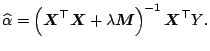 |
Figure 5.3 shows a smoothing spline fitted to the fuel economy dataset. Clearly, the fit is very similar to the local regression fit in Fig. 5.2. This situation is common for smoothing problems with a single predictor variable; with comparably chosen smoothing parameters, local regression and smoothing spline methods produce similar results. On the other hand, kernel methods can struggle to produce acceptable results, even on relatively simple datasets.
Regression splines begin by choosing a set of knots (typically, much smaller than the number of data points), and a set of basis functions spanning a set of piecewise polynomials satisfying continuity and smoothness constraints.
Let the knots be
![]() with
with
![]() and
and
![]() . A linear spline basis is
. A linear spline basis is
![$\displaystyle f_j(x) = \begin{cases}\displaystyle \frac{x-v_{j-1}}{v_j-v_{j-1}}...
..._{j+1}-v_j} & v_j < x \le v_{j+1}\\ [3mm] 0 & {\text{otherwise}} \end{cases}{};$](img4085.gif) |
The linear spline basis functions have discontinuous derivatives, and so the resulting fit may have a jagged appearance. It is more common to use piecewise cubic splines, with the basis functions having two continuous derivatives. See Chap. 3 of [26] for a more detailed discussion of regression splines and basis functions.
Orthogonal series methods represent the data with respect to a series of orthogonal basis functions, such as sines and cosines. Only the low frequency terms are retained. The book [6] provides a detailed discussion of this approach to smoothing.
Suppose the ![]() are equally spaced;
are equally spaced; ![]() . Consider the basis
functions
. Consider the basis
functions
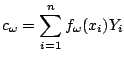 |
|
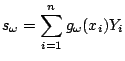 |
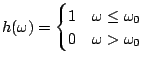 |
Orthogonal series are widely used to model time series, where the
coefficients
![]() and
and
![]() may have a physical
interpretation: non-zero coefficients indicate the presence of cycles
in the data. A limitation of orthogonal series approaches is that they
are more difficult to apply when the
may have a physical
interpretation: non-zero coefficients indicate the presence of cycles
in the data. A limitation of orthogonal series approaches is that they
are more difficult to apply when the ![]() are not equally spaced.
are not equally spaced.