Thus far, we have described dimension reduction methods for multidimensional data, where there are no distinctions among variables. However, there are times when we must analyze multidimensional data in which a variable is a response variable and others are explanatory variables. Regression analysis is usually used for the data. Dimension reduction methods of explanatory variables are introduced below.
Regression analysis is one of the fundamental methods used for data
analysis. A response variable ![]() is estimated by a function of
explanatory variables
is estimated by a function of
explanatory variables
![]() , a
, a ![]() -dimensional vector. An immediate
goal of ordinary regression analysis is to find the function of
-dimensional vector. An immediate
goal of ordinary regression analysis is to find the function of
![]() .
When there are many explanatory variables in the data set, it is
difficult to stably calculate the regression coefficients. An
approach to reducing the number of explanatory variables is
explanatory variable selection, and there are many studies on variable
selection. Another approach is to project the explanatory variables on
a lower dimensional space that nearly estimates the response variable.
.
When there are many explanatory variables in the data set, it is
difficult to stably calculate the regression coefficients. An
approach to reducing the number of explanatory variables is
explanatory variable selection, and there are many studies on variable
selection. Another approach is to project the explanatory variables on
a lower dimensional space that nearly estimates the response variable.
Sliced Inverse Regression (SIR),
which was proposed by [11], is a method that can be employed to
reduce explanatory variables with linear projection. SIR finds linear
combinations of explanatory variables that are a reduction for
non-linear regression. The original SIR algorithm, however, cannot
derive suitable results for some artificial data with trivial
structures. Li also developed another algorithm, SIR2, which uses the
conditional estimation
![]() . However, SIR2 is also
incapable of finding trivial structures for another type of data.
. However, SIR2 is also
incapable of finding trivial structures for another type of data.
We hope that projection pursuit can be used for finding linear combinations of explanatory variables. A new SIR method with projection pursuit (SIRpp) is described here. We also present a numerical example of the proposed method.
SIR is based on the model (SIR model):
The purpose of SIR is to estimate the vectors
![]() for which
this model holds. If we obtain
for which
this model holds. If we obtain
![]() , we can reduce the
dimension of
, we can reduce the
dimension of
![]() to
to ![]() . Hereafter, we shall refer to any linear
combination of
. Hereafter, we shall refer to any linear
combination of
![]() as the effective dimensional reduction
(e.d.r.) direction.
as the effective dimensional reduction
(e.d.r.) direction.
[11] proposed an algorithm for finding e.d.r. directions, and it was named SIR. However, we refer to the algorithm as SIR1 to distinguish it from the SIR model.
The main idea of SIR1 is to use
![]() .
.
![]() is contained in
the space spanned by e.d.r. directions, but there is no guarantee that
is contained in
the space spanned by e.d.r. directions, but there is no guarantee that
![]() will span the space. For example, in Li, if
will span the space. For example, in Li, if
![]() then
then
![]() .
.
Hereafter, it is assumed that the distribution of
![]() is standard
normal distribution:
is standard
normal distribution:
![]() . If not, standardize
. If not, standardize
![]() by
affine transformation. In addition,
by
affine transformation. In addition,
![]() is presumed
without loss of generality. We can choose
is presumed
without loss of generality. We can choose
![]() such that
such that
![]()
![]() is a basis for
is a basis for
![]() .
.
Since the distribution of
![]() is
is ![]() , the distribution of
, the distribution of
![]() is also
is also
![]() . The density function of
. The density function of
![]() is
is
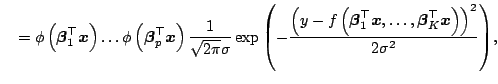 |
The conditional density function is
Thus,
![]() is
separated into the normal distribution part
is
separated into the normal distribution part
![]() and the non-normal distribution
part
and the non-normal distribution
part ![]() .
.
Projection Pursuit is an excellent method for finding non-normal parts, so we adopt it for SIR.
Here we show the algorithm for the SIR model with projection pursuit
(SIRpp). The algorithm for the data
![]() is
as follows:
is
as follows:
Two models of the multicomponent are used:
The squared multiple correlation coefficient between the projected
variable
![]() and the space
and the space ![]() spanned by ideal
e.d.r. directions:
spanned by ideal
e.d.r. directions:
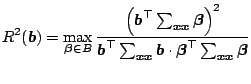 |
(6.10) |
Table 6.1 shows the mean and the standard deviation (in
parentheses) of
![]() and
and
![]() of
four SIR algorithms for
of
four SIR algorithms for ![]() , and
, and ![]() , after
, after ![]() replicates.
SIR2 cannot reduce the explanatory variables from the first example.
The result of the second example is very interesting. SIR1 finds the
asymmetric e.d.r. direction, but, does not find the symmetric
e.d.r. direction. Conversely, SIR2 finds only the symmetric
e.d.r. direction. SIRpp can detect both of the e.d.r. directions.
replicates.
SIR2 cannot reduce the explanatory variables from the first example.
The result of the second example is very interesting. SIR1 finds the
asymmetric e.d.r. direction, but, does not find the symmetric
e.d.r. direction. Conversely, SIR2 finds only the symmetric
e.d.r. direction. SIRpp can detect both of the e.d.r. directions.
| SIR |
SIR |
SIRpp | ||||||
| H |
|
|
|
|
|
|
||
| |
0.92 | 0.77 | 0.96 | 0.20 | 0.97 | 0.78 | ||
| (0.04) | (0.11) | (0.03) | (0.21) | (0.02) | (0.15) | |||
| 0.93 | 0.81 | 0.92 | 0.10 | 0.95 | 0.79 | |||
| (0.03) | (0.09) | (0.09) | (0.12) | (0.04) | (0.13) | |||
| 0.92 | 0.76 | 0.83 | 0.11 | 0.95 | 0.75 | |||
| (0.04) | (0.18) | (0.19) | (0.13) | (0.07) | (0.18) | |||
The SIRpp algorithm performs well in finding the e.d.r. directions; however, the algorithm requires more computing power. This is one part of projection pursuit for which the algorithm is time consuming.
| SIR |
SIR |
SIRpp | ||||||
| H |
|
|
|
|
|
|
||
| |
0.97 | 0.12 | 0.92 | 0.01 | 0.92 | 0.88 | ||
| (0.02) | (0.14) | (0.04) | (0.10) | (0.05) | (0.11) | |||
| 0.97 | 0.12 | 0.90 | 0.05 | 0.88 | 0.84 | |||
| (0.02) | (0.15) | (0.06) | (0.07) | (0.08) | (0.13) | |||
| 0.97 | 0.12 | 0.85 | 0.05 | 0.84 | 0.73 | |||
| (0.02) | (0.14) | (0.09) | (0.06) | (0.10) | (0.22) | |||
![\includegraphics[width=8cm]{text/3-6/func3.eps}](img4543.gif)
|