In the previous section, we discussed linear methods i.e. methods for dimension reduction through the use of linear projections. We will now move on to nonlinear methods for dimension reduction. First, we will describe a generalized principal component analysis (GPCA) method that is a nonlinear extension of PCA. Algebraic curve fitting methods will then be mentioned for a further extension of GPCA. Finally, we will introduce principal curves i.e. the parametric curves that pass through the middle of the data.
As long as data have a near-linear structure, the singularities of the data can be pointed out using PCA. On the contrary, if data have a nonlinear structure, GPCA will not be adequate for drawing conclusions regarding the nature of the data. To overcome this difficulty, GPCA has been proposed by [3], whereby fitting functions to the data points can be discovered.
Suppose that we have observations of ![]() variables
variables
![]() on each of
on each of ![]() individuals. Let
individuals. Let
![]() be
be ![]() real-valued functions of the original
variables.
real-valued functions of the original
variables.
The aim of GPCA is to discover a new set of variables (or functions
of
![]() ), as denoted by
), as denoted by
![]() , which are mutually
uncorrelated and whose variances decrease, from first to last. Each
, which are mutually
uncorrelated and whose variances decrease, from first to last. Each
![]() is considered to be a linear combination of
is considered to be a linear combination of
![]() , so that
, so that
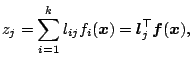 |
PCA is a special case of GPCA: real-valued functions
![]() are
reduced to
are
reduced to
![]() .
.
Quadratic principal component analysis (QPCA) is specified by the following functions:
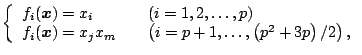 |
QPCA for two dimensional data is defined by
Most GPCA methods are not invariant under orthogonal transformations and/or the translations (parallel transformations) of a coordinate system, though PCA is invariant under them. For example, QPCA is not invariant under them. The expression ''the method is invariant'' in this subsection means that the results of the method are never changed in the original coordinate by coordinate transformation. In the following, the determination of the GPCA methods that are invariant under the orthogonal transformations of a coordinate system will be described in the case of two variables. Translations of a coordinate system are disregarded here because the data can be standardized to have a zero mean vector.
Hereafter, let us assume the following conditions:
A GPCA method is referred to as ''invariant'' if its results in the
original coordinate system are not changed by the orthogonal
transformation of a coordinate system. It can be mathematically
described as follows. For any orthogonal coordinate transformation:
![]() ,
,
The GPCA method specified by
![]() is invariant under an
orthogonal transformation, if and only if the matrix
is invariant under an
orthogonal transformation, if and only if the matrix ![]() is an
orthogonal matrix for any orthogonal matrix
is an
orthogonal matrix for any orthogonal matrix ![]() . The proof will be
described below. If the method is invariant,
. The proof will be
described below. If the method is invariant, ![]() can be taken as
can be taken as
[12] derived a theorem on invariant GPCA.
![$\displaystyle \left\{ \begin{array}{lcl}
f_{2i-1}(x,y) &=& g_i\left(\sqrt{x^2+...
...4\end{array} \right)y^4x^{N_i-4}
-\ldots \right)\\ [4mm]
\end{array}
\right.$](img4364.gif) |
|
The above theorem can be extended for use with GPCA methods for
![]() -dimensional data because invariant GPCA for
-dimensional data because invariant GPCA for ![]() -dimensional data
methods are invariant under the rotations of any pair of two variables
and the reverse is also true.
-dimensional data
methods are invariant under the rotations of any pair of two variables
and the reverse is also true.
We will show some set of functions for invariant GPCA here.
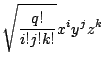 |
|
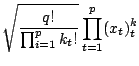 |
|
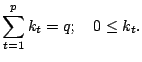 |
Next, we will discuss a method involving algebraic curve and surface fitting to multidimensional data.
The principal component line minimizes the sum of squared deviations
in each of the variables. The PCA cannot find non-linear structures in
the data. GPCA is used to discover an algebraic curve fitted to data;
the function ![]() defined by the ''smallest'' eigenvalue is
considered to be one of the fitting functions to the data. However,
it is difficult to interpret algebraic curves statistically derived
form GPCA.
defined by the ''smallest'' eigenvalue is
considered to be one of the fitting functions to the data. However,
it is difficult to interpret algebraic curves statistically derived
form GPCA.
We will now describe methods for estimating the algebraic curve or surface that minimizes the sum of squares of perpendicular distances from multidimensional data.
[18] developed an algorithm for discovering the algebraic curve for which the sum of approximate squares distances between data points and the curve is minimized. The approximate squares distance does not always agree with the exact squares distance. Mizuta ([13], [14]) presented an algorithm for evaluating the exact distance between the data point and the curve, and have presented a method for algebraic curve fitting with exact distances. In this subsection, we describe the method of algebraic surface fitting with exact distances. The method of the algebraic curve fitting is nearly identical to that of surface fitting, and is therefore omited here.
A ![]() -dimensional algebraic curve or surface is the set of zeros of
-dimensional algebraic curve or surface is the set of zeros of
![]() -polynomials
-polynomials
![]() on
on
![]() ,
,
In the case of ![]() and
and ![]() ,
,
![]() is a surface:
is a surface:
Hereafter, we will primarily discuss this case.
The distance from a point
![]() to the surface
to the surface
![]() is usually
defined by
is usually
defined by
It was said that the distance between a point and the algebraic curve
or surface cannot be computed using direct methods. Thus, Taubin
proposed an approximate distance from
![]() to
to
![]() ([18]). The point
([18]). The point
![]() that approximately minimizes
the distance
that approximately minimizes
the distance
![]() , is given by
, is given by
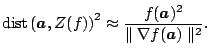 |
In the following, we present a method for calculating the distance
between a point
![]() and an algebraic
surface
and an algebraic
surface
![]() .
.
If ![]() is the nearest point to the point
is the nearest point to the point
![]() on
on
![]() ,
, ![]() satisfies the
following simultaneous equations:
satisfies the
following simultaneous equations:
Equations (6.1) can be solved using the Newton-Rapson method:
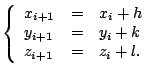 |
One of the important points to consider when applying the
Newton-Rapson method is to compute an initial point. We have a good
initial point:
![]() .
.
When
![]() , (6.2)
are
, (6.2)
are
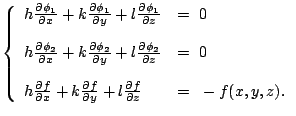 |
We have already described the method for calculating the distance between a point and a surface.
The problem of finding a fitting surface that minimizes the sum of the distances from data points can therefore be solved by using an optimization method without derivatives. However, for computing efficiency, the partial derivatives of the sum of squares of distances from data with the coefficients of an algebraic curve are derived.
In general, a polynomial ![]() in a set is denoted by
in a set is denoted by
Let
![]() be
be ![]() data
points within the space. The point in
data
points within the space. The point in
![]() that minimizes the
distance from
that minimizes the
distance from
![]() is denoted by
is denoted by
![]() .
.
The sum of squares of distances is
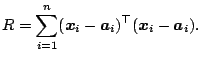 |
The only matter left to discuss is a solution for
![]() and
and
![]() . Hereafter, the subscript
. Hereafter, the subscript ![]() is
omitted. By the derivative of both sides of
is
omitted. By the derivative of both sides of
![]() with respect to
with respect to
![]() , we obtain
, we obtain
Since
![]() is on the normal line from
is on the normal line from
![]() ,
,
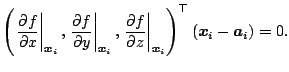 |
Equations (6.5) and (6.6) are
simultaneous linear equations in four variables
![]() and
and
![]() . We then obtain
. We then obtain
![]() and
and
![]() at
at
![]() .
By (6.4), we have the partial differentiation of
.
By (6.4), we have the partial differentiation of
![]() with respect to
with respect to ![]() .
.
Therefore, we can obtain the algebraic curve that minimizes the sum of squares of distances from data points with the Levenberg-Marquardt method.
Although algebraic curves can fit the data very well, they usually contain points far remote from the given data set. In 1994, [9] and [20] independently developed algorithms for a bounded (closed) algebraic curve with approximate squares distance. We will now introduce the definition and properties of a bounded algebraic curve.
![]() is referred to as bounded
if there exists a constant
is referred to as bounded
if there exists a constant ![]() such that
such that
![]() . For example, it is clear that
. For example, it is clear that
![]() is bounded, but
is bounded, but
![]() is not bounded.
is not bounded.
[9] defined
![]() to be stably bounded
if a small perturbation of the coefficients of the polynomial leaves
its zero set bounded. An algebraic curve
to be stably bounded
if a small perturbation of the coefficients of the polynomial leaves
its zero set bounded. An algebraic curve
![]() is
bounded but not stably bounded because
is
bounded but not stably bounded because
![]() is not bounded for any
is not bounded for any
![]() .
.
Let ![]() be the form of degree
be the form of degree ![]() of a polynomial
of a polynomial ![]() :
:
![]() . The leading form of a polynomial
. The leading form of a polynomial
![]() of degree
of degree ![]() is defined by
is defined by ![]() . For example, the
leading form of
. For example, the
leading form of
![]() is
is
![]() .
.
These definitions and theorem for algebraic curves are valid for algebraic surfaces. Hereafter, we will restrict our discussion to algebraic surfaces.
We parameterize the set of all polynomials of degree ![]() and the set
of polynomials that induce (stably) bounded algebraic surfaces. In
general, a polynomial
and the set
of polynomials that induce (stably) bounded algebraic surfaces. In
general, a polynomial ![]() of degree
of degree ![]() with
with ![]() parameters can be
denoted by
parameters can be
denoted by
![]() , where
, where
![]() are the
parameters of the polynomial.
are the
parameters of the polynomial.
For example, all of the polynomials of degree ![]() can be
represented by
can be
represented by
For stably bounded algebraic curves of degree ![]() ,
,
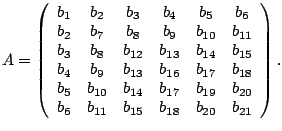 |
Here we will show a numerical example of the algebraic surface and bounded algebraic surface fitting methods.
The data in this example is three-dimensional data of size ![]() . The
. The
![]() points nearly lie on a closed cylinder (Fig. 6.1).
The result of GPCA is set for an initial surface and the method is
used to search for a fitting algebraic surface of degree
points nearly lie on a closed cylinder (Fig. 6.1).
The result of GPCA is set for an initial surface and the method is
used to search for a fitting algebraic surface of degree ![]() (Figs. 6.2, 6.3 and 6.4). The value
of
(Figs. 6.2, 6.3 and 6.4). The value
of ![]() is
is ![]() .
.
Figure 6.5 presents the result of a bounded
algebraic surface fitting the same data. The value of ![]() is
is
![]() , and is greater than that of unbounded fitting. The
bounded surface, however, directly reveals the outline of the data.
, and is greater than that of unbounded fitting. The
bounded surface, however, directly reveals the outline of the data.
In this subsection, we have discussed algebraic surface fitting to multidimensional data. Two sets of algebraic surfaces were described: an unbounded algebraic surface and a bounded algebraic surface. This method can be extended for use with any other family of algebraic surfaces.
[19] proposed the approximate distance of order ![]() and
presented algorithms for rasterizing algebraic curves. The proposed
algorithm for exact distance can also be used for rasterizing
algebraic curves and surfaces. [15] has successfully developed
a program for rasterizing them with exact distances.
and
presented algorithms for rasterizing algebraic curves. The proposed
algorithm for exact distance can also be used for rasterizing
algebraic curves and surfaces. [15] has successfully developed
a program for rasterizing them with exact distances.
Curve fitting to data is an important method for data analysis. When we obtain a fitting curve for data, the dimension of the data is nonlinearly reduced to one dimension. [5] proposed the concept of a principal curve and developed a concrete algorithm to find the principal curve, which is represented by a parametric curve. We can therefore obtain a new nonlinear coordinate for the data using the principal curve.
First, we will define principal curves for a ![]() -dimensional
distribution function
-dimensional
distribution function
![]() , rather than a dataset.
, rather than a dataset.
The expectation of ![]() with density function
with density function ![]() in
in ![]() is denoted
by
is denoted
by ![]() . The parametric curve within the
. The parametric curve within the ![]() -dimensional space is
represented by
-dimensional space is
represented by
![]() , where
, where ![]() is the parameter.
is the parameter.
For each point
![]() in
in ![]() , the parameter
, the parameter ![]() of the nearest
point on the curve
of the nearest
point on the curve
![]() is denoted by
is denoted by
![]() ,
which is referred to as the projection index. The projection
index, which is different from projection index in projection pursuit,
is defined as follows:
,
which is referred to as the projection index. The projection
index, which is different from projection index in projection pursuit,
is defined as follows:
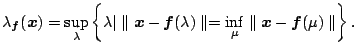 |
The curve
![]() is referred to as the principal curve of
density function
is referred to as the principal curve of
density function ![]() , if
, if
The principal curves of a given distribution are not always unique. For example, two principal components of the two-dimensional normal distribution are principal curves.
The algorithm for finding the principal curves of a distribution is:
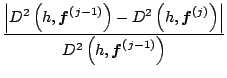 |
In the Expectation Step, calculate the expectation with respect to
the distribution ![]() of the set of
of the set of
![]() satisfying
satisfying
![]() and substitute
and substitute
![]() for it. In the Projection Step, project data
points in
for it. In the Projection Step, project data
points in ![]() to the curve
to the curve
![]() and
assign
and
assign
![]() .
.
For actual data analysis, only a set of data points is given and the
distribution is unknown. [5] also proposed an algorithm with
which to derive the principal curve for given ![]() -dimensional data of
size
-dimensional data of
size ![]() :
:
![]() . In this case, the
principal curves are represented by lines determined by
. In this case, the
principal curves are represented by lines determined by ![]() points
points
![]() .
.