To illustrate the GLM in practice we recall
Example 1 on credit worthiness.
The credit data set that we use
[13] contains ![]() observations on consumer credits
and a variety of explanatory variables. We have selected a subset
of eight explanatory variables for the following examples.
observations on consumer credits
and a variety of explanatory variables. We have selected a subset
of eight explanatory variables for the following examples.
The model for credit
worthiness is based on the idea that default can be predicted
from the individual and loan characteristics.
We consider criteria as age, information on previous loans, savings,
employment and house ownership to characterize the credit applicants.
Amount and duration of the loan are prominent features of the granted loans.
Some descriptive statistics
can be found in Table 7.3. We remark that we have categorized
the durations (months) into intervals since most of the realizations
are multiples of ![]() or
or ![]() months.
months.
| Variable | Yes | No | (in %) | |
| 30.0 | 70.0 | |||
| PREVIOUS (no problem) | 38.1 | 61.9 | ||
| EMPLOYED ( |
93.8 | 6.2 | ||
| DURATION |
21.6 | 78.4 | ||
| DURATION |
18.7 | 81.3 | ||
| DURATION |
22.4 | 77.6 | ||
| DURATION |
23.0 | 77.0 | ||
| SAVINGS | 18.3 | 81.7 | ||
| PURPOSE (buy a car) | 28.4 | 71.6 | ||
| HOUSE (owner) | 15.4 | 84.6 | ||
| Min. | Max. | Mean | Std.Dev. | |
| AMOUNT (in DM) | 250 | 18424 | 3271.248 | 2822.752 |
| AGE (in years) | 19 | 75 | 35.542 | 11.353 |
We are at the first place interested in estimating the probability
of credit default in dependence of the explanatory variables
![]() .
Recall that for binary
.
Recall that for binary ![]() it holds
it holds
![]() Our first approach is a GLM with logit link such that
Our first approach is a GLM with logit link such that
![]() .
.
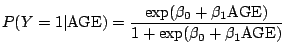
From the table we see that the estimated
coefficient of
![]() has a negative sign. Since the link function and its
inverse are strictly monotone increasing, we can conclude that the probability
of default must thus be decreasing with increasing
has a negative sign. Since the link function and its
inverse are strictly monotone increasing, we can conclude that the probability
of default must thus be decreasing with increasing
![]() .
Figure 7.1 shows on the left frequency barplots of
.
Figure 7.1 shows on the left frequency barplots of
![]() separately for
separately for ![]() and
and ![]() . From the observed frequencies
we can recognize clearly the decreasing propensity to default.
The right graph in Fig. 7.1 displays the estimated
probabilities
. From the observed frequencies
we can recognize clearly the decreasing propensity to default.
The right graph in Fig. 7.1 displays the estimated
probabilities
![]() using the fitted logit model
which are indeed decreasing.
using the fitted logit model
which are indeed decreasing.
The ![]() -values
(
-values
(
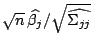 ) show
that the coefficient of
) show
that the coefficient of
![]() is significantly different from
is significantly different from ![]() while
the estimated constant is not. The test that
is used here is an approximative
while
the estimated constant is not. The test that
is used here is an approximative ![]() -test such that
-test such that
![]() -quantile
of the standard normal can be used as critical value. This implies that at
the usual
-quantile
of the standard normal can be used as critical value. This implies that at
the usual ![]() level we compare the absolute value of the
level we compare the absolute value of the ![]() -value with
-value with
![]() .
.
A more general approach to test for the significance of
![]() is to compare
the fitted model with a model that involves only a constant
default probability. Typically software packages report the deviance of
this model as null deviance or similar.
In our case we find a null deviance
of
is to compare
the fitted model with a model that involves only a constant
default probability. Typically software packages report the deviance of
this model as null deviance or similar.
In our case we find a null deviance
of ![]() at
at ![]() degrees of freedom. If we apply the LR test
statistic (7.16)
to compare the null deviance to the model deviance of
degrees of freedom. If we apply the LR test
statistic (7.16)
to compare the null deviance to the model deviance of ![]() at
at ![]() degrees of freedom, we find that constant model is clearly
rejected at a significance level of
degrees of freedom, we find that constant model is clearly
rejected at a significance level of
![]() .
.
| Variable | Coefficient | |
| constant | ||
|
|
||
| Deviance | ||
| df | ||
| AIC | ||
| Iterations |
![\includegraphics[width=117mm,clip]{text/3-7/abb/mm1}](img4766.gif) |
Models using different link functions cannot be directly compared as the
link functions might be differently scaled. In our binary response model
for example a logit or a probit
link function may be reasonable. However,
the variance parameter of the standard logistic distribution is ![]() whereas that of the standard normal is
whereas that of the standard normal is ![]() . We therefore need to rescale
one of the link functions in order to compare the resulting model fits.
Figure 7.2 shows the standard logistic cdf
(the inverse logit link) against the cdf of
. We therefore need to rescale
one of the link functions in order to compare the resulting model fits.
Figure 7.2 shows the standard logistic cdf
(the inverse logit link) against the cdf of
![]() . The functions
in the left graph of Fig. 7.2 are hardly distinguishable.
If we zoom in (right graph) we see that the logistic cdf vanishes to zero
at the left boundary at a lower rate. This holds similarly for the right boundary
and explains the ability of logit models
to (slightly) better handle the case of extremal observations.
. The functions
in the left graph of Fig. 7.2 are hardly distinguishable.
If we zoom in (right graph) we see that the logistic cdf vanishes to zero
at the left boundary at a lower rate. This holds similarly for the right boundary
and explains the ability of logit models
to (slightly) better handle the case of extremal observations.
![\includegraphics[width=117mm,clip]{text/3-7/abb/mm2}](img4769.gif)
|
A Newton-Raphson iteration
(instead of the Fisher scoring reported in Table 7.5)
does give somewhat different coefficients but returns nearly the
same value of the deviance (![]() for Newton-Raphson versus
for Newton-Raphson versus ![]() for Fisher scoring).
for Fisher scoring).
| Variable | Coefficient | ||
| (original) | (rescaled) | ||
| constant | |||
|
|
|||
| Deviance | |||
| df | |||
| AIC | |||
| Iterations | 4 | (Fisher Scoring) | |
The next two examples intend to analyze if the fit could be
improved by using a nonlinear function on
![]() instead
of
instead
of
![]() . Two principally different
approaches are
possible:
. Two principally different
approaches are
possible:
| Variable | Coefficient | Coefficient | ||
| constant | ||||
|
|
||||
| AGE**2 |
|
|
||
| AGE**3 |
|
|||
| Deviance | ||||
| df | ||||
| AIC | ||||
| Iterations |
![\includegraphics[width=117mm,clip]{text/3-7/abb/mm3}](img4803.gif)
|
To incorporate a possible nonlinear impact of a variable in
the index function, we can alternatively categorize this
variable. Another term for this is the construction of dummy
variables. The most classical form of the categorization
consists in using a design matrix that sets a value of ![]() in the column
corresponding to the category if the category is true and
in the column
corresponding to the category if the category is true and
![]() otherwise. To obtain a full rank design matrix we omit
one column for the reference category. In our example we leave
out the first category which means that all estimated coefficients
have to be compared to the zero coefficient of the reference
category. Alternative categorization setups are given
by omitting the constant, the sum coding (restrict the coefficients
to sum up to
otherwise. To obtain a full rank design matrix we omit
one column for the reference category. In our example we leave
out the first category which means that all estimated coefficients
have to be compared to the zero coefficient of the reference
category. Alternative categorization setups are given
by omitting the constant, the sum coding (restrict the coefficients
to sum up to ![]() ), and the Helmert coding.
), and the Helmert coding.
Frequency
barplots for the intervals and estimated default probabilities
are displayed in Fig. 7.4.
The resulting coefficients
for this model are listed in Table 7.7. We see here
that all coefficient estimates are negative. This means, keeping in
mind that the group of youngest credit applicants is the reference,
that all applicants from other age groups have an (estimated) lower
default probability. However, we do not have a true decrease in the default
probabilities with
![]() since the coefficients do not form a decreasing
sequence. In the range from age
since the coefficients do not form a decreasing
sequence. In the range from age ![]() to
to ![]() we find two local minima and maxima
for the estimated default probabilities.
we find two local minima and maxima
for the estimated default probabilities.
It is interesting to note that the deviance of the categorized
![]() fit is the smallest that we obtained up to now. This is explained
by the fact that we have fitted the most flexible model here. Unfortunately,
this flexibility pays with the number of parameters. The
AIC criterion as a compromise between goodness-of-fit and number
of parameters states that all previous fitted models are preferable.
Nevertheless, categorization is a valuable tool to explore if there
are nonlinear effects. A related technique is local
regression smoothing which is shortly reviewed in Sect. 7.5.8.
fit is the smallest that we obtained up to now. This is explained
by the fact that we have fitted the most flexible model here. Unfortunately,
this flexibility pays with the number of parameters. The
AIC criterion as a compromise between goodness-of-fit and number
of parameters states that all previous fitted models are preferable.
Nevertheless, categorization is a valuable tool to explore if there
are nonlinear effects. A related technique is local
regression smoothing which is shortly reviewed in Sect. 7.5.8.
| Variable | Coefficients | |
| constant | ||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
| Deviance | ||
| df | ||
| AIC | ||
| Iterations |
![\includegraphics[width=117mm,clip]{text/3-7/abb/mm4}](img4833.gif)
|
The estimation of default probabilities and the prediction of credit default should incorporate more than only one explanatory variable. Before fitting the full model with all available information, we discuss the modeling of interaction effects.
Table 7.8
shows the results for all three fitted models. The model with
quadratic and interaction terms has the smallest AIC of the three
fits. Pairwise LR tests show, however, that the largest of the
three models is not significantly better
than the model without the interaction term. The obtained
surface on
![]() and
and
![]() from the quadratic+interaction fit is displayed
in Fig. 7.5.
from the quadratic+interaction fit is displayed
in Fig. 7.5.
| Variable | Coefficient | Coefficient | Coefficient | |||
| constant | ||||||
|
|
||||||
|
|
|
|
||||
|
|
|
|
|
|||
|
|
|
|
||||
|
|
|
|
||||
| Deviance | ||||||
| df | ||||||
| AIC | ||||||
| Iterations |
![\includegraphics[width=117mm,clip]{text/3-7/abb/mm5}](img4878.gif)
|
Let us remark that interaction terms can also be defined for categorical variables. In this case interaction is modeled by including dummy variables for all possible combinations of categories. This may largely increase the number of parameters to estimate.
After fitting the full model we have
run an automatic stepwise model selection based on AIC.
This reveals that the insignificant terms
![]() and EMPLOYED should be
omitted. The fitted coefficients for this final model are displayed in the
fourth column of Table 7.9.
and EMPLOYED should be
omitted. The fitted coefficients for this final model are displayed in the
fourth column of Table 7.9.
| Variable | Coefficient | Coefficient | ||
| constant | ||||
|
|
||||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|||
| PREVIOUS | ||||
| EMPLOYED | ||||
| DURATION |
||||
| DURATION |
||||
| DURATION |
||||
| DURATION |
||||
| SAVINGS | ||||
| PURPOSE | ||||
| HOUSE | ||||
| Deviance | ||||
| df | ||||
|
|
||||
| Iterations |