![$\displaystyle f(y_i,\theta_i,\psi) = \exp\left[\frac{w_i \{y\theta-b(\theta)\}}{a(\psi)}
+ c(y,\psi,w_i)\right].$](img4939.gif)
For further reading on GLM we refer to the textbooks of [11], [27] and [19] (the latter with a special focus on STATA). [36, Chap. 7] and [15] present the topic of generalized linear models in a very compact form. [7], [2], [9], and [5] are standard references for analyzing categorical responses. We recommend the monographs of [13] and [25] for a detailed introduction to GLM with a focus on multivariate, longitudinal and spatial data. In the following sections we will shortly review some specific variants and enhancements of the GLM.
Prior weights can be incorporated to the generalized linear model by considering the exponential density in the form
![$\displaystyle f(y_i,\theta_i,\psi) = \exp\left[\frac{w_i \{y\theta-b(\theta)\}}{a(\psi)}
+ c(y,\psi,w_i)\right].$](img4939.gif)
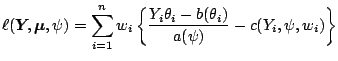
The weights ![]() can be
can be ![]() or
or ![]() in the simplest case that one wants to
exclude specific observations from the estimation. The typical case
of applying weights is the case of repeated independent realizations.
in the simplest case that one wants to
exclude specific observations from the estimation. The typical case
of applying weights is the case of repeated independent realizations.
Overdispersion may occur in one-parameter exponential families
where the variance is supposed to be a function of the mean.
This concerns in particular the binomial or Poisson families
where we have ![]() and
and
![]() or
or
![]() ,
respectively. Overdispersion means that the actually
observed variance from the data is larger than the variance imposed
by the model. The source for this may be a lack of independence
in the data or a misspecification of the model. One possible
approach is to use alternative models that allows for a nuisance
parameter in the variance, as an example think of the negative
binomial instead of the Poisson distribution.
For detailed discussions on overdispersion
see [7] and [1].
,
respectively. Overdispersion means that the actually
observed variance from the data is larger than the variance imposed
by the model. The source for this may be a lack of independence
in the data or a misspecification of the model. One possible
approach is to use alternative models that allows for a nuisance
parameter in the variance, as an example think of the negative
binomial instead of the Poisson distribution.
For detailed discussions on overdispersion
see [7] and [1].
Let us remark that in the case that the distribution of
![]() itself is unknown but its two first moments
can be specified, the quasi-likelihood function may replace
the log-likelihood function. This means we still assume that
itself is unknown but its two first moments
can be specified, the quasi-likelihood function may replace
the log-likelihood function. This means we still assume that
A multinomial model (or nominal
logistic regression) is applied
if the response for each observation ![]() is one out of more than
two alternatives (categories). For identification one of the categories
has to be chosen as reference category; without loss of generality
we use here the first category.
Denote by
is one out of more than
two alternatives (categories). For identification one of the categories
has to be chosen as reference category; without loss of generality
we use here the first category.
Denote by ![]() the probability
the probability
![]() , then we can consider
the logits with respect to the first category, i.e.
, then we can consider
the logits with respect to the first category, i.e.
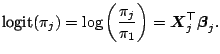
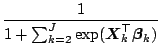 |
|||
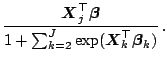 |
If the categories are ordered in some natural way then this additional information can be taken into account. A latent variable approach leads to the cumulative logit model or the ordered probit model. We refer here to [11, Sect. 8.4] and [18, Chap. 21] for ordinal logistic regression and ordered probit analysis, respectively.
The simplest form of a contingency table
| Category | |||||
| Frequency |
with one factor and a predetermined sample size ![]() of observations
is appropriately described by a multinomial distribution and can hence
be fitted by the multinomial logit model introduced in
Sect. 7.5.4. We could be for instance be interested in
comparing the trivial model
of observations
is appropriately described by a multinomial distribution and can hence
be fitted by the multinomial logit model introduced in
Sect. 7.5.4. We could be for instance be interested in
comparing the trivial model
![]() to the model
to the model
![]() (again we use the first category as reference). As before
further explanatory variables can be included into the model.
(again we use the first category as reference). As before
further explanatory variables can be included into the model.
Two-way or higher dimensional contingency tables involve a large variety of possible models. Let explain this with the help of the following two-way setup:
| Category | |||||
| 1 |
|
||||
| 2 |
|
||||
|
|
|||||
|
|
|
|
Here we assume to have two factors, one with realizations
![]() ,
the other with realizations
,
the other with realizations
![]() .
If the
.
If the ![]() are independent Poisson variables with parameters
are independent Poisson variables with parameters
![]() , then their sum is a Poisson variable with parameter
, then their sum is a Poisson variable with parameter
![]() . The Poisson assumption implies that the number of observations
. The Poisson assumption implies that the number of observations
![]() is a random variable. Conditional on
is a random variable. Conditional on ![]() , the joint distribution of
the
, the joint distribution of
the ![]() is the multinomial distribution. Without additional explanatory
variables, one is typically interested in estimating models of the
type
is the multinomial distribution. Without additional explanatory
variables, one is typically interested in estimating models of the
type
Survival data are characterized by non-negative observations which
typically have a skewed distribution. An additional complication
arises due to the fact that the observation period may end before
the individual fails such that censored data may occur. The exponential
distribution with density
![]() is a very simple example for a survival distribution.
In this special case the survivor function (the probability to survive
beyond
is a very simple example for a survival distribution.
In this special case the survivor function (the probability to survive
beyond ![]() ) is given by
) is given by
![]() and the hazard
function (the probability of death within
and the hazard
function (the probability of death within ![]() and
and ![]() after
survival up to
after
survival up to ![]() ) equals
) equals
![]() . Given additional
explanatory variables this function is typically modeled by
. Given additional
explanatory variables this function is typically modeled by
Clustered data in relation to regression models mean that data from known groups (``clusters'') are observed. Often these are the result of repeated measurements on the same individuals at different time points. For example, imagine the analysis of the effect of a medical treatment on patients or the repeated surveying of households in socio-economic panel studies. Here, all observations on the same individual form a cluster. We speak of longitudinal or panel data in that case. The latter term is typically used in the econometric literature.
When using clustered data we have to take into account that observations from the same cluster are correlated. Using a model designed for independent data may lead to biased results or at least significantly reduce the efficiency of the estimates.
A simple individual model equation could be written as follows:
There is a waste amount of literature which deals with many different possible model specifications. A comprehensive resource for linear and nonlinear mixed effect models (LME, NLME) for continuous responses is [30]. The term ``mixed'' here refers to the fact that these models include additional random and/or fixed effect components to allow for correlation within and heterogeneity between the clusters.
For generalized linear mixed models (GLMM), i.e. clustered observations with
responses from GLM-type distribution, several approaches are possible.
For repeated observations, [24] and [38] propose to use
generalized estimating equations
(GEE) which result in
a quasi-likelihood estimator. They show that the correlation matrix
of
![]() , the response observations from one cluster, can be
replaced by a ``working correlation''
as long as the moments
of
, the response observations from one cluster, can be
replaced by a ``working correlation''
as long as the moments
of
![]() are correctly specified. Useful working correlations
depend on a small number of parameters. For longitudinal data
an autoregressive working correlation can be used for example.
For more details on GEE see also the monograph by
[10]. In the econometric literature
longitudinal or panel data are analyzed with a focus on
continuous and binary responses. Standard references for econometric
panel data analyses are [22] and
[4].
Models for clustered data with complex hierarchical structure are often denoted
as multilevel models. We refer to the monograph of
[16] for an overview.
are correctly specified. Useful working correlations
depend on a small number of parameters. For longitudinal data
an autoregressive working correlation can be used for example.
For more details on GEE see also the monograph by
[10]. In the econometric literature
longitudinal or panel data are analyzed with a focus on
continuous and binary responses. Standard references for econometric
panel data analyses are [22] and
[4].
Models for clustered data with complex hierarchical structure are often denoted
as multilevel models. We refer to the monograph of
[16] for an overview.
Nonparametric components can be incorporated into the GLM at different places. For example, it is possible to estimate a single index model
Local regression in combination with likelihood-based estimation is introduced in [26]. This concerns models of the form
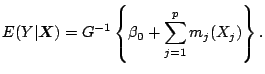
![\includegraphics[width=117mm,clip]{text/3-7/abb/mm6}](img4999.gif)
|
Some more material on semiparametric regression can be found in Chaps. III.5 and III.10 of this handbook. For a detailed introduction to semiparametric extensions of GLM we refer to the textbooks by [21], [20], [31], and [17].