



Next: 7.4 Practical Aspects
Up: 7. Generalized Linear Models
Previous: 7.2 Model Characteristics
Subsections
Recall that the least squares estimator for the ordinary
linear regression model is also the maximum-likelihood
estimator in the case of normally distributed error terms.
By assuming that the distribution of 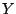 belongs to the exponential
family it is possible to derive maximum-likelihood
estimates for the coefficients of a GLM. Moreover we will see that
even though the estimation needs a numerical approximation, each step
of the iteration can be given by a weighted least squares fit.
Since the weights are varying during the iteration the likelihood
is optimized by an iteratively reweighted least
squares
algorithm.
belongs to the exponential
family it is possible to derive maximum-likelihood
estimates for the coefficients of a GLM. Moreover we will see that
even though the estimation needs a numerical approximation, each step
of the iteration can be given by a weighted least squares fit.
Since the weights are varying during the iteration the likelihood
is optimized by an iteratively reweighted least
squares
algorithm.
7.3.1 Properties of the Exponential Family
To derive the details of the maximum-likelihood algorithm we need
to discuss some properties of the probability mass or
density function
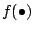 . For the sake of brevity we consider
. For the sake of brevity we consider
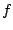 to be a density function in the following derivation.
However, the conclusions
will hold for a probability mass function as well.
to be a density function in the following derivation.
However, the conclusions
will hold for a probability mass function as well.
First, we start from the fact that
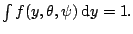 Under suitable regularity conditions (it is possible to
exchange differentiation and integration) this implies
Under suitable regularity conditions (it is possible to
exchange differentiation and integration) this implies
where
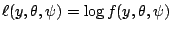 denotes the
log-likelihood function.
The function derivative of
denotes the
log-likelihood function.
The function derivative of 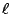 with respect to
with respect to 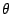 is typically called the score function for which it is known that
This and taking first and second derivatives of (7.1)
results in
such that we can conclude
is typically called the score function for which it is known that
This and taking first and second derivatives of (7.1)
results in
such that we can conclude
Note that as a consequence from (7.1) the expectation
of 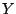 depends only on the parameter of interest
depends only on the parameter of interest 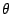 .
We also assume that the factor
.
We also assume that the factor 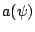 is identical
over all observations.
is identical
over all observations.
7.3.2 Maximum-Likelihood and Deviance Minimization
As pointed out before the estimation method of choice
for
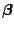 is maximum-likelihood. As an alternative
the literature refers to the minimization of the
deviance.
We will see during the following derivation
that both approaches are identical.
is maximum-likelihood. As an alternative
the literature refers to the minimization of the
deviance.
We will see during the following derivation
that both approaches are identical.
Suppose that we have observed a sample of independent pairs
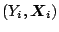 where
where
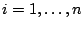 .
For a more compact notation denote now the vector of all
response observations by
.
For a more compact notation denote now the vector of all
response observations by
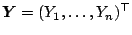 and their conditional expectations (given
and their conditional expectations (given
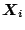 ) by
) by
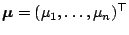 .
Recall that we study
.
Recall that we study
The sample log-likelihood of the vector
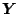 is then given by
is then given by
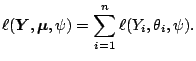 |
(7.4) |
Here 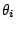 is a function of
is a function of
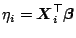 and we use
and we use
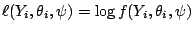 to denote the
individual log-likelihood contributions for all
observations
to denote the
individual log-likelihood contributions for all
observations 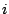 .
.
Example 5 (Normal log-likelihood)
For normal responses
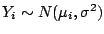 we have
we have
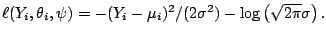 This gives the sample log-likelihood
This gives the sample log-likelihood
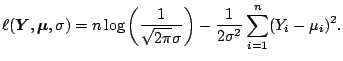 |
(7.5) |
Obviously, maximizing this log-likelihood
is equivalent to minimizing the least squares criterion.
Example 6 (Bernoulli log-likelihood)
The calculation in Example 3 shows that
the individual log-likelihoods for the binary responses
equal
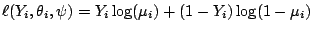 .
This leads to
.
This leads to
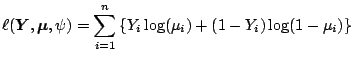 |
(7.6) |
for the sample version.
The deviance defines an alternative objective function for
optimization. Let us first introduce the scaled
deviance which is defined as
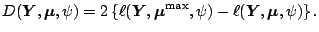 |
(7.7) |
Here
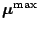 (which typically equals
(which typically equals
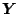 ) is the vector that
maximizes the saturated model, i.e. the
function
) is the vector that
maximizes the saturated model, i.e. the
function
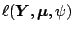 without imposing any restriction
on
without imposing any restriction
on
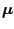 . Since the term
. Since the term
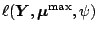 does not depend
on the parameter
does not depend
on the parameter
 we see that indeed
the minimization of the scaled deviance is equivalent
to the maximization of the sample log-likelihood (7.4).
we see that indeed
the minimization of the scaled deviance is equivalent
to the maximization of the sample log-likelihood (7.4).
If we now plug-in the exponential family form (7.1)
into (7.4) we obtain
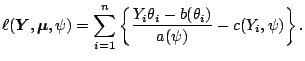 |
(7.8) |
Obviously, neither 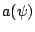 nor
nor
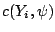 depend on the
unknown parameter vector
depend on the
unknown parameter vector
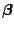 . Therefore, it is sufficient
to consider
. Therefore, it is sufficient
to consider
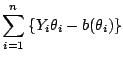 |
(7.9) |
for the maximization. The deviance analog of (7.9) is the
(non-scaled) deviance function
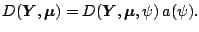 |
(7.10) |
The (non-scaled) deviance
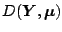 can be seen as
the GLM equivalent of the residual sum of squares
(RSS) in linear regression as it compares the log-likelihood
can be seen as
the GLM equivalent of the residual sum of squares
(RSS) in linear regression as it compares the log-likelihood 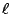 for the ``model''
for the ``model'' 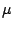 with the maximal achievable
value of
with the maximal achievable
value of 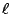 .
.
7.3.3 Iteratively Reweighted Least Squares Algorithm
We will now minimize the deviance with respect to
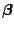 .
If we denote the gradient of (7.10) by
.
If we denote the gradient of (7.10) by
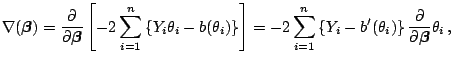 |
(7.11) |
our optimization problem consists in solving
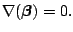 |
(7.12) |
Note that this is (in general) a nonlinear system of equations in
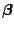 and an iterative solution has to be computed. The smoothness of the link
function allows us to compute the Hessian of
and an iterative solution has to be computed. The smoothness of the link
function allows us to compute the Hessian of
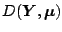 ,
which we denote by
,
which we denote by
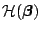 .
Now a Newton-Raphson
algorithm can be applied which determines the optimal
.
Now a Newton-Raphson
algorithm can be applied which determines the optimal
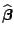 using the following iteration
steps:
using the following iteration
steps:
A variant of the Newton-Raphson is the
Fisher scoring algorithm
that replaces the Hessian by its expectation with respect to the observations
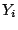 :
To find simpler representations for these iterations, recall that we
have
:
To find simpler representations for these iterations, recall that we
have
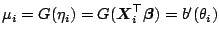 .
By taking the derivative of the right hand term with
respect to
.
By taking the derivative of the right hand term with
respect to
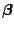 this implies
Using that
this implies
Using that
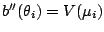 as established in (7.3)
and taking derivatives again, we finally obtain
as established in (7.3)
and taking derivatives again, we finally obtain
From this we can express the gradient and the Hessian of the
deviance by
The expectation of
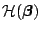 in the Fisher scoring algorithm equals
in the Fisher scoring algorithm equals
Let us consider only the Fisher scoring algorithm
for the moment. We define the weight matrix
and the vectors
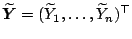 ,
,
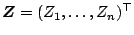 by
Denote further by
by
Denote further by
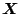 the design matrix given by the rows
the design matrix given by the rows
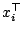 .
Then, the Fisher scoring iteration step for
.
Then, the Fisher scoring iteration step for
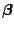 can be rewritten as
can be rewritten as
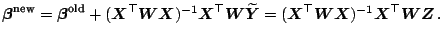 |
(7.13) |
This immediately shows that each Fisher scoring iteration step
is the result of a weighted least squares regression of
the adjusted dependent
variables 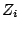 on
the explanatory variables
on
the explanatory variables
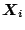 .
Since the weights are recalculated in each step
we speak of the iteratively
reweighted least squares (IRLS) algorithm. For the Newton-Raphson
algorithm a representation equivalent to (7.13) can be found,
only the weight matrix
.
Since the weights are recalculated in each step
we speak of the iteratively
reweighted least squares (IRLS) algorithm. For the Newton-Raphson
algorithm a representation equivalent to (7.13) can be found,
only the weight matrix
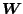 differs.
differs.
The iteration will be stopped when the parameter estimate and/or the
deviance do not change significantly anymore.
We denote the final parameter estimate by
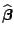 .
.
Let us first note two special cases for the algorithm:
- In the linear regression model,
where we have
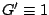 and
and
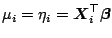 ,
no iteration is necessary. Here the ordinary least squares
estimator gives the explicit solution of (7.12).
,
no iteration is necessary. Here the ordinary least squares
estimator gives the explicit solution of (7.12).
- In the case of a canonical link function we have
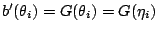 and hence
and hence
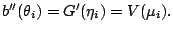 Therefore the Newton-Raphson
and the Fisher scoring algorithms coincide.
Therefore the Newton-Raphson
and the Fisher scoring algorithms coincide.
There are several further remarks on the algorithm which
concern in particular starting values and the computation of
relevant terms for the statistical analysis:
The resulting estimator
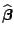 has an
asymptotic normal distribution (except of course for the normal
linear regression case when this is
an exact normal distribution).
has an
asymptotic normal distribution (except of course for the normal
linear regression case when this is
an exact normal distribution).
Theorem 1
Under regularity conditions we have for the estimated
coefficient vector
As a consequence for the scaled deviance and the
log-likelihood approximately hold
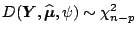 and
and
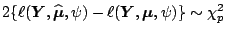 .
.
For details on the necessary conditions see for example
[12].
Note also that the asymptotic covariance
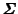 for the coefficient estimator
for the coefficient estimator
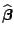 is the inverse of the Fisher information matrix, i.e.
is the inverse of the Fisher information matrix, i.e.
Since
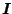 can be estimated by the negative Hessian of the log-likelihood
or its expectation, this suggests the estimator
can be estimated by the negative Hessian of the log-likelihood
or its expectation, this suggests the estimator
Using the estimated covariance we are able to test hypotheses
about the components of
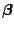 .
.
For model choice between two nested models
a likelihood ratio test
(LR test) is used.
Assume that
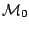 (
(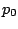 parameters) is a submodel of the model
parameters) is a submodel of the model
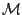 (
(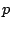 parameters) and that
we have estimated them as
parameters) and that
we have estimated them as
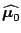 and
and
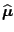 .
For one-parameter exponential families (without a nuisance parameter
.
For one-parameter exponential families (without a nuisance parameter 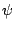 )
we use that asymptotically
)
we use that asymptotically
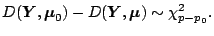 |
(7.16) |
The left hand side of (7.16) is a function of the
ratio of the two likelihoods deviance difference equals
minus twice the log-likelihood difference.
In a two-parameter exponential family (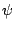 is to be estimated)
one can approximate the likelihood ratio test statistic by
is to be estimated)
one can approximate the likelihood ratio test statistic by
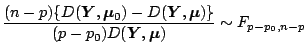 |
(7.17) |
using the analog to the normal linear regression case
([36]), Chap. 7.
Model selection
procedures for possibly non-nested models
can be based on Akaike's information
criterion [3]
or Schwarz' Bayes information criterion [32]
where again  denotes the number of estimated parameters. For
a general overview on model selection techniques see also
Chap. III.1 of this handbook.
denotes the number of estimated parameters. For
a general overview on model selection techniques see also
Chap. III.1 of this handbook.




Next: 7.4 Practical Aspects
Up: 7. Generalized Linear Models
Previous: 7.2 Model Characteristics
![]() belongs to the exponential
family it is possible to derive maximum-likelihood
estimates for the coefficients of a GLM. Moreover we will see that
even though the estimation needs a numerical approximation, each step
of the iteration can be given by a weighted least squares fit.
Since the weights are varying during the iteration the likelihood
is optimized by an iteratively reweighted least
squares
algorithm.
belongs to the exponential
family it is possible to derive maximum-likelihood
estimates for the coefficients of a GLM. Moreover we will see that
even though the estimation needs a numerical approximation, each step
of the iteration can be given by a weighted least squares fit.
Since the weights are varying during the iteration the likelihood
is optimized by an iteratively reweighted least
squares
algorithm.
![]() . For the sake of brevity we consider
. For the sake of brevity we consider
![]() to be a density function in the following derivation.
However, the conclusions
will hold for a probability mass function as well.
to be a density function in the following derivation.
However, the conclusions
will hold for a probability mass function as well.
![]() Under suitable regularity conditions (it is possible to
exchange differentiation and integration) this implies
Under suitable regularity conditions (it is possible to
exchange differentiation and integration) this implies
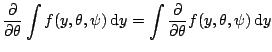
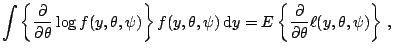
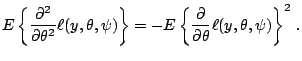
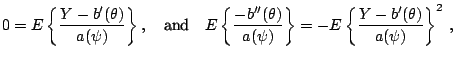
![]() is maximum-likelihood. As an alternative
the literature refers to the minimization of the
deviance.
We will see during the following derivation
that both approaches are identical.
is maximum-likelihood. As an alternative
the literature refers to the minimization of the
deviance.
We will see during the following derivation
that both approaches are identical.
![]() where
where
![]() .
For a more compact notation denote now the vector of all
response observations by
.
For a more compact notation denote now the vector of all
response observations by
![]() and their conditional expectations (given
and their conditional expectations (given
![]() ) by
) by
![]() .
Recall that we study
.
Recall that we study
![]() .
If we denote the gradient of (7.10) by
.
If we denote the gradient of (7.10) by
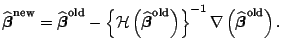
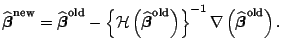
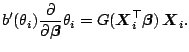
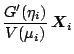
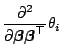
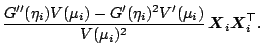
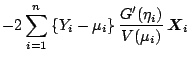
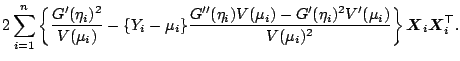
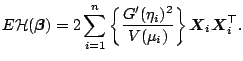
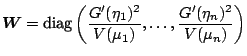
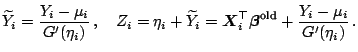
![]() .
.
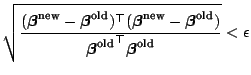
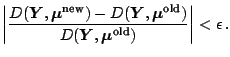
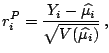
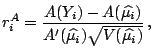
![]() has an
asymptotic normal distribution (except of course for the normal
linear regression case when this is
an exact normal distribution).
has an
asymptotic normal distribution (except of course for the normal
linear regression case when this is
an exact normal distribution).
![]() for the coefficient estimator
for the coefficient estimator
![]() is the inverse of the Fisher information matrix, i.e.
is the inverse of the Fisher information matrix, i.e.
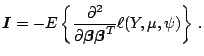
![$\displaystyle \widehat{{\boldsymbol{\mathit{\Sigma}}}} = a(\widehat{\psi})\left...
...i,\text{last}})} \right\}\boldsymbol{X}_i \boldsymbol{X}_i^\top \right]^{-1}\,.$](img4729.gif)
![]() (
(![]() parameters) is a submodel of the model
parameters) is a submodel of the model
![]() (
(![]() parameters) and that
we have estimated them as
parameters) and that
we have estimated them as
![]() and
and
![]() .
For one-parameter exponential families (without a nuisance parameter
.
For one-parameter exponential families (without a nuisance parameter ![]() )
we use that asymptotically
)
we use that asymptotically