Subsections

• 2.3.1 The Multiple Recursive Generator
• 2.3.2 The Lattice Structure
• 2.3.3 MRG Implementation Techniques
• 2.3.4 Combined MRGs and LCGs
• 2.3.5 Jumping Ahead
• 2.3.6 Linear Recurrences With Carry

2.3 Linear Recurrences Modulo $m$

2.3.1 The Multiple Recursive Generator

The most widely used RNGs are based on the linear recurrence

$$x_i = (a_1 x_{i-1} + \cdots + a_k x_{i-k}) \,{\mathop{\text{mod}}}\, m\;,$$ (2.2)

where $m$ and $k$ are positive integers called the modulus and the order, and the coefficients $a_1,\ldots,a_k$ are in  ${\mathbb{Z}}_m$, interpreted as the set $\{0,\ldots, m-1\}$ on which all operations are performed with reduction modulo $m$. The state at step $i$ is $s_i = \boldsymbol{x}_i = (x_{i-k+1},\ldots,x_i)^{{{\sf T}}}$. When $m$ is a prime number, the finite ring ${\mathbb{Z}}_m$ is a finite field and it is possible to choose the coefficients $a_j$ so that the period length reaches $\rho = m^k-1$ (the largest possible value) ([31]). This maximal period length is achieved if and only if the characteristic polynomial of the recurrence, $P(z) = z^k - a_1 z^{k-1} - \cdots - a_k$, is a primitive polynomial over ${\mathbb{Z}}_m$, i.e., if and only if the smallest positive integer $\nu$ such that $(z^\nu \,{\mathop{\text{mod}}}\, P(z))\, {\mathop{\text{mod}}}\,m = 1$ is $\nu = m^k-1$. [31] explains how to verify this for a given $P(z)$. For $k>1$, for $P(z)$ to be a primitive polynomial, it is necessary that $a_k$ and at least another coefficient $a_j$ be nonzero. Finding primitive polynomials of this form is generally easy and they yield the simplified recurrence:

$$x_n = (a_r x_{n-r} + a_k x_{n-k})\, {\mathop{\text{mod}}}\, m\;.$$ (2.3)

A multiple recursive generator (MRG) uses (2.2) with a large value of $m$ and defines the output as $u_i = x_i / m$. For $k=1$, this is the classical linear congruential generator (LCG). In practice, the output function is modified slightly to make sure that $u_i$ never takes the value 0 or $1$ (e.g., one may define $u_i = (x_i + 1) / (m+1)$, or $u_i = x_i/(m+1)$ if $x_i>0$ and $u_i = m/(m+1)$ otherwise) but to simplify the theoretical analysis, we will follow the common convention of assuming that $u_i = x_i / m$ (in which case $u_i$ does take the value 0 occasionally).

2.3.2 The Lattice Structure

Let $\boldsymbol{e}_i$ denote the $i$th unit vector in $k$ dimensions, with a $1$ in position $i$ and 0's elsewhere. Denote by $x_{i,0}, x_{i,1}, x_{i,2},\ldots$ the values of $x_0, x_1, x_2,\ldots$ produced by the recurrence (2.2) when the initial state $\boldsymbol{x}_0$ is $\boldsymbol{e}_i$. An arbitrary initial state $\boldsymbol{x}_0 = (z_1,\ldots,z_k)^{{{\sf T}}}$ can be written as the linear combination $z_1 \boldsymbol{e}_1 + \cdots + z_k \boldsymbol{e}_k$ and the corresponding sequence is a linear combination of the sequences $(x_{i,0}, x_{i,1}, \ldots)$, with reduction of the coordinates modulo $m$. Reciprocally, any such linear combination reduced modulo $m$ is a sequence that can be obtained from some initial state $\boldsymbol{x}_0 \in {\mathcal{S}} = {\mathbb{Z}}_m^k$. If we divide everything by $m$ we find that for the MRG, for each $t\ge 1$, $\Psi_t = L_t \cap [0,1)^t$ where

$$L_t = \left\{\boldsymbol{v} = \sum_{i=1}^t z_i \boldsymbol{v}_i \;\mid\; z_i\in{\mathbb{Z}}\right\}\;,$$

is a $t$-dimensional lattice in ${\mathbb{R}}^t$, with basis

$$\boldsymbol{v}_1 = (1,0,\ldots,0, x_{1,k}, \ldots, x_{1,t-1})^{{{\sf T}}}/m$$

$$\vdots \vdots$$

$$\boldsymbol{v}_k = (0,0,\ldots,1, x_{k,k}, \ldots, x_{k,t-1})^{{{\sf T}}}/m$$

$$\boldsymbol{v}_{k+1} = (0,0,\ldots,0, 1, \ldots, 0)^{{{\sf T}}}$$

$$\vdots \vdots$$

$$\boldsymbol{v}_{t} = (0,0,\ldots,0, 0, \ldots, 1)^{{{\sf T}}}\;.$$

For $t\le k$, $L_t$ contains all vectors whose coordinates are multiples of $1/m$. For $t > k$, it contains a fraction $m^{k-t}$ of those vectors.

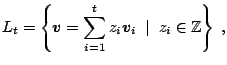This lattice structure implies that the points of $\Psi_t$ are distributed according to a very regular pattern, in equidistant parallel hyperplanes. Graphical illustrations of this, usually for LCGs, can be found in a myriad of papers and books; e.g., [23,31,34], and [40]. Define the dual lattice to $L_t$ as

$$L_t^{\ast} = \{\boldsymbol{h} \in {\mathbb{R}}^t : \boldsymbol{h}^{{{\sf T}}} \boldsymbol{v} \in{\mathbb{Z}} \quad \boldsymbol{v}\in L_t\}\;.$$

Each $\boldsymbol{h}\in L_t^{\ast}$ is a normal vector that defines a family of equidistant parallel hyperplanes, at distance $1/\Vert\boldsymbol{h}\Vert_2$ apart, and these hyperplanes cover all the points of $L_t$ unless $\boldsymbol{h}$ is an integer multiple of some other vector $\boldsymbol{h}'\in L_t^{\ast}$. Therefore, if $\ell_t$ is the euclidean length of a shortest non-zero vector $\boldsymbol{h}$ in $L_t^{\ast}$, then there is a family of hyperplanes at distance $1/\ell_t$ apart that cover all the points of $L_t$. A small $\ell_t$ means thick slices of empty space between the hyperplanes and we want to avoid that. A large $\ell_t$ means a better (more uniform) coverage of the unit hypercube by the point set $\Psi_t$. Computing the value of $1/\ell_t$ is often called the spectral test ([31,21]).

The lattice property holds as well for the point sets $\Psi_I$ formed by values at arbitrary lags defined by a fixed set of indices $I = \{i_1,\cdots, i_t\}$. One has $\Psi_I = L_I \cap [0,1)^t$ for some lattice $L_I$, and the largest distance between successive hyperplanes for a family of hyperplanes that cover all the points of $L_I$ is $1/\ell_I$, where $\ell_I$ is the euclidean length of a shortest nonzero vector in $L_I^{\ast}$, the dual lattice to $L_I$.

The lattice $L_I$ and its dual can be constructed as explained in [10] and [49]. Finding the shortest nonzero vector in a lattice with basis $\boldsymbol{v}_1,\ldots,\boldsymbol{v}_t$ can be formulated as an integer programming problem with a quadratic objective function:

$$\Vert\boldsymbol{v}\Vert^2 = \sum_{i=1}^t \sum_{j=1}^t z_i \boldsymbol{v}_i^{{{\sf T}}} \boldsymbol{v}_j z_j$$

subject to $z_1,\ldots,z_t$ integers and not all zero. This problem can be solved by a branch-and-bound algorithm ([20,49,88]).

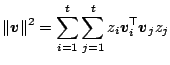For any given dimension $t$ and $m^k$ points per unit of volume, there is an absolute upper bound on the best possible value of $\ell_I$ ([8,31,42]). Let $\ell_t^{\ast}(m^k)$ denote such an upper bound. To define a figure of merit that takes into account several sets $I$, in different numbers of dimensions, it is common practice to divide $\ell_I$ by an upper bound, in order to obtain a standardized value between 0 and $1$, and then take the worst case over a given class ${\mathcal{J}}$ of sets $I$. This gives a figure of merit of the form

$$M_{{\mathcal{J}}} = \min_{I\in {\mathcal{J}}}\; \ell_I / \ell_{\vert I\vert}^{\ast}(m^k)\;.$$

A value of $M_{{\mathcal{J}}}$ too close to zero means that $L_I$ has a bad lattice structure for at least one of the selected sets $I$. We want a value as close to $1$ as possible. Computer searches for good MRGs with respect to this criterion have been reported by [47,46,41], for example. In most cases, ${\mathcal{J}}$ was simply the sets of the form $I = \{1,\ldots,t\}$ for $t\le t_1$, where $t_1$ was an arbitrary integer ranging from $8$ to $45$. [52] also consider the small dimensional sets $I$ with indices not too far apart. They suggest taking ${\mathcal{J}} = \{\{0,1,\ldots,i\} : i < t_1\} \cup \{\{i_1,i_2\} : 0 = i_1 < i_2 < t_2\} \cup \cdots \cup \{\{i_1,\ldots,i_d\} : 0 = i_1 < \ldots < i_d < t_d\}$ for some positive integers $d, t_1,\ldots, t_d$. We could also take a weighted average instead of the minimum in the definition of  $M_{{\mathcal{J}}}$.

An important observation is that for $t > k$, the $t$-dimensional vector $\boldsymbol{h}=(-1,a_1,\ldots,a_k,0,\ldots,0)^{{{\sf T}}}$ always belongs to $L_t^{\ast}$, because for any vector $\boldsymbol{v}\in L_t$, the first $k+1$ coordinates of $m \boldsymbol{v}$ must satisfy the recurrence (2.2), which implies that $(-1,a_1,\ldots,a_k,0,\ldots,0)\boldsymbol{v}$ must be an integer. Therefore, one always has $\ell_t^2 \le 1 + a_1^2 + \cdots + a_k^2$. Likewise, if $I$ contains 0 and all indices $j$ such that $a_{k-j}\not=0$, then $\ell_I^2 \le 1 + a_1^2 + \cdots + a_k^2$ ([39]). This means that the sum of squares of the coefficients $a_j$ must be large if we want to have any chance that the lattice structure be good.

Contructing MRGs with only two nonzero coefficients and taking these coefficients small has been a very popular idea, because this makes the implementation easier and faster ([14,31]). However, MRGs thus obtained have a bad structure. As a worst-case illustration, consider the widely-available additive or subtractive lagged-Fibonacci generator, based on the recurrence (2.2) where the two coefficients $a_r$ and $a_k$ are both equal to $\pm 1$. In this case, whenever $I$ contains $\{0, k-r, k\}$, one has $\ell_I^2 \le 3$, so the distance between the hyperplanes is at least $1/\sqrt{3}$. In particular, for $I = \{0, k-r, k\}$, all the points of $\Psi_I$ (aside from the zero vector) are contained in only two planes! This type of structure can have a dramatic effect on certain simulation problems and is a good reason for staying away from these lagged-Fibonacci generators, regardless of their parameters.

A similar problem occurs for the ''fast MRG'' proposed by [14], based on the recurrence

$$x_i = (-x_{i-1} + a~x_{i-k})\, {\mathop{\text{mod}}}\, m = ((m-1)x_{i-1} + a~x_{i-k})\, {\mathop{\text{mod}}}\, m\;,$$

with $a^2 < m$. If $a$ is small, the bound $\ell_I^2 \le 1 + a^2$ implies a bad lattice structure for $I = \{0, k-1, k\}$. A more detailed analysis by [63] shows that this type of generator cannot have a good lattice structure even if the condition $a^2 < m$ is removed. Another special case proposed by [15] has the form

$$x_i = a\left(x_{i-j_2} + \cdots + x_{i-j_t}\right) \,{\mathop{\text{mod}}}\, m\;.$$ (2.4)

In this case, for $I = \{0, k-j_{t-1}, \ldots, k-j_2, k\}$, the vectors $(1,a,\ldots,a)$ and $(a^{\ast},1,\ldots,1)$ both belong to the dual lattice  $L_I^{\ast}$, where $a^{\ast}$ is the multiplicative inverse of $a$ modulo $m$. So neither $a$ nor $a^{\ast}$ should be small.

To get around this structural problem when $I$ contains certain sets of indices, [70] and [31] recommend to skip some of the output values in order to break up the bad vectors. For the lagged-Fibonacci generator, for example, one can output $k$ successive values produced by the recurrence, then skip the next $d$ values, output the next $k$, skip the next $d$, and so on. A large value of $d$ (e.g., $d=5k$ or more) may get rid of the bad structure, but slows down the generator. See [98] for further discussion.

2.3.3 MRG Implementation Techniques

The modulus $m$ is often taken as a large prime number close to the largest integer directly representable on the computer (e.g., equal or near $2^{31}-1$ for 32-bit computers). Since each $x_{i-j}$ can be as large as $m-1$, one must be careful in computing the right side of (2.2) because the product $a_j x_{i-j}$ is typically not representable as an ordinary integer. Various techniques for computing this product modulo $m$ are discussed and compared by [21,48,41], and [56]. Note that if $a_j = m - a'_j > 0$, using $a_j$ is equivalent to using the negative coefficient $-a'_j$, which is sometimes more convenient from the implementation viewpoint. In what follows, we assume that $a_j$ can be either positive or negative.

One approach is to perform the arithmetic modulo $m$ in $64$-bit (double precision) floating-point arithmetic ([41]). Under this representation, assuming that the usual IEEE floating-point standard is respected, all positive integers up to $2^{53}$ are represented exactly. Then, if each coefficient $a_j$ is selected to satisfy $\vert a_j\vert (m-1) \le 2^{53}$, the product $\vert a_j\vert x_{i-j}$ will always be represented exactly and $z_j = \vert a_j\vert x_{i-j}\, {\mathop{\text{mod}}}\, m$ can be computed by the instructions

$$y = \vert a_j\vert x_{i-j}\;; \quad z_j = y - m \lfloor\, y/m\rfloor\;.$$

Similarly, if $(\vert a_1\vert + \cdots + \vert a_k\vert) (m-1) \le 2^{53}$, $a_1 x_{i-1} + \cdots + a_k x_{i-k}$ will always be represented exactly.

A second technique, called approximate factoring ([48]), uses only the integer representation and works under the condition that $\vert a_j\vert = i$ or $\vert a_j\vert = \lfloor m/i\rfloor$ for some integer $i < \sqrt{m}$. One precomputes $q_j = \lfloor m/\vert a_j\vert \rfloor$ and $r_j = m\,{\mathop{\text{mod}}}\, \vert a_j\vert$. Then, $z_j = \vert a_j\vert x_{i-j}\, {\mathop{\text{mod}}}\, m$ can be computed by

$$y = \lfloor x_{i-j} / q_j \rfloor\;; \quad z = \vert a_j\vert (x_{i-j} - y q_j) - y r_j\;;$$

$$\quad z < 0 \quad z_j = z + m \quad z_j = z\;.$$

All quantities involved in these computations are integers between $-m$ and $m$, so no overflow can occur if $m$ can be represented as an ordinary integer (e.g., $m < 2^{31}$ on a $32$-bit computer).

The powers-of-two decomposition approach selects coefficients $a_j$ that can be written as a sum or difference of a small number of powers of $2$ ([99,56,62]). For example, one may take $a_j = \pm 2^q \pm 2^r$ and $m = 2^e - h$ for some positive integers $q$, $r$, $e$, and $h$. To compute $y = 2^q x {\mathop{\text{mod}}} m$, decompose $x = z_0 + 2^{e-q} z_1$ (where $z_0 = x \,$mod$\, 2^{e-q}$) and observe that

$$y = 2^q(z_0 + 2^{e-q}z_1) \mod (2^e -h) = (2^q z_0 + hz_1) \mod (2^e - h)\;.$$

Suppose now that

$$h < 2^q \quad h (2^q -(h+1)2^{-e+q}) < m\;.$$ (2.5)

Then, $2^q z_0 < m$ and $h z_1 < m$, so $y$ can be computed by shifts, masks, additions, subtractions, and a single multiplication by $h$. Intermediate results never exceed $2m-1$. Things simplify further if $q=0$ or $q=1$ or $h=1$. For $h=1$, $y$ is obtained simply by swapping the blocks of bits $z_0$ and $z_1$ ([99]). It has been pointed out by [56] that LCGs with parameters of the form $m = 2^e-1$ and $a = \pm 2^q \pm 2^r$ have bad statistical properties because the recurrence does not ''mix the bits'' well enough. However, good and fast MRGs can be obtained via the power-of-two decomposition method, as explained in [62].

Another interesting idea for improving efficiency is to take all nonzero coefficients $a_j$ equal to the same constant $a$ ([72,15]). Then, computing the right side of (2.2) requires a single multiplication. [15] provide specific parameter sets and concrete implementations for MRGs of this type, for prime $m$ near $2^{31}$, and $k=102$, $120$, and ${1511}$.

One may be tempted to take $m$ equal to a power of two, say $m=2^e$, because then the '' mod$\, m$'' operation is much easier: it suffices to keep the $e$ least significant bits and mask-out all others. However, taking a power-of-two modulus is not recommended because it has several strong disadvantages in terms of the quality of the RNG ([35,40]). In particular, the least significant bits have very short periodicity and the period length of the recurrence (2.2) cannot exceed $(2^k-1) 2^{e-1}$ if $k>1$, and $2^{e-2}$ if $k=1$ and $e\ge 4$. The maximal period length achievable with $k=7$ and $m=2^{31}$, for example, is more than $2^{180}$ times smaller than the maximal period length achievable with $k=7$ and $m=2^{31}-1$ (a prime number).

2.3.4 Combined MRGs and LCGs

The conditions that make MRG implementations run faster (e.g., only two nonzero coefficients both close to zero) are generally in conflict with those required for having a good lattice structure and statistical robustness. Combined MRGs are one solution to this problem. Consider $J$ distinct MRGs evolving in parallel, based on the recurrences

$$x_{j,i} = \left(a_{j,1} x_{j,i-1} + \cdots + a_{j,k} x_{j,i-k}\right) \mod m_j\;;$$ (2.6)

where $a_{j,k}\not=0$, for $j=1,\ldots,J$. Let $\delta_1,\ldots,\delta_J$ be arbitrary integers,

$$z_i = \left(\delta_1 x_{1,i} + \cdots + \delta_J x_{J,i}\right) \mod m_1\;, \quad u_i = z_i/m_1\;,$$ (2.7)

and

$$w_i = \left(\delta_1 x_{1,i}/ m_1 + \cdots + \delta_J x_{J,i}/ m_J\right) \mod 1\;.$$ (2.8)

This defines two RNGs, with output sequences $\{u_i,\, i\ge 0\}$ and $\{w_i,\, i\ge 0\}$.

Suppose that the $m_j$ are pairwise relatively prime, that $\delta_j$ and $m_j$ have no common factor for each $j$, and that each recurrence (2.6) is purely periodic with period length $\rho_j$. Let $m = m_1\cdots m_J$ and let $\rho$ be the least common multiple of $\rho_1,\ldots,\rho_J$. Under these conditions, the following results have been proved by [61] and [37]: (a) the sequence (2.8) is exactly equivalent to the output sequence of a MRG with (composite) modulus $m$ and coefficients $a_j$ that can be computed explicitly as explained in [37]; (b) the two sequences in (2.7) and (2.8) have period length $\rho$; and (c) if both sequences have the same initial state, then $u_i = w_i + \epsilon_i$ where $\max_{i\ge 0} \vert\epsilon_i\vert$ can be bounded explicitly by a constant $\epsilon$ which is very small when the $m_j$ are close to each other.

Thus, these combined MRGs can be viewed as practical ways of implementing an MRG with a large $m$ and several large nonzero coefficients. The idea is to cleverly select the components so that: (1) each one is easy to implement efficiently (e.g., has only two small nonzero coefficients) and (2) the MRG that corresponds to the combination has a good lattice structure. If each $m_j$ is prime and if each component $j$ has maximal period length $\rho_j = m_j^k-1$, then each $\rho_j$ is even and $\rho$ cannot exceed $\rho_1 \cdots \rho_J/2^{J-1}$. Tables of good parameters for combined MRGs of different sizes that reach this upper bound are given in [41] and [62], together with C implementations.

2.3.5 Jumping Ahead

The recurrence (2.2) can be written in matrix form as

$$\boldsymbol{x}_i = \boldsymbol{A} \boldsymbol{x}_{i-1} \mod m = \... ...\ a_k & a_{k-1} & \cdots & a_1 \cr \end{pmatrix} \boldsymbol{x}_{i-1} \mod m\;.$$

To jump ahead directly from $\boldsymbol{x}_i$ to $\boldsymbol{x}_{i+\nu}$, for an arbitrary integer $\nu$, it suffices to exploit the relationship

$$\boldsymbol{x}_{i+\nu} = \boldsymbol{A}^\nu \boldsymbol{x}_{i} \mod m = (\boldsymbol{A}^\nu \mod m) \boldsymbol{x}_{i} \mod m\;.$$

If this is to be done several times for the same $\nu$, the matrix $\boldsymbol{A}^\nu \mod m$ can be precomputed once for all. For a large $\nu$, this can be done in $O(\log_2 \nu)$ matrix multiplications via a standard divide-and-conquer algorithm ([31]):

$$\boldsymbol{A}^\nu \mod m = \begin{cases}(\boldsymbol{A}^{\nu/2} ... ...(\boldsymbol{A}^{\nu-1} \mod m) \mod m & \text{if $\nu$\ is odd}\;. \end{cases}$$

2.3.6 Linear Recurrences With Carry

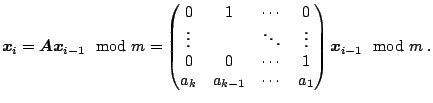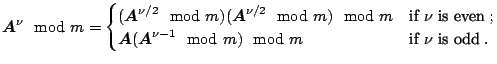These types of recurrences were introduced by [73] to obtain a large period even when $m$ is a power of two (in which case the implementation may be faster). They were studied and generalized by [90,9,11], and [24]. The basic idea is to add a carry to the linear recurrence (2.2). The general form of this RNG, called multiply-with-carry (MWC), can be written as

$$x_i = (a_1 x_{i-1} + \cdots + a_k x_{i-k} + c_{i-1}) d \mod b\;,$$ (2.9)

$$c_i = \lfloor (a_0 x_i + a_1 x_{i-1} + \cdots + a_k x_{i-k} + c_{i-1})/ b \rfloor\;,$$ (2.10)

$$u_i = \sum_{\ell=1}^\infty x_{i+\ell-1} b^{-\ell}\;,$$ (2.11)

where $b$ is a positive integer (e.g., a power of two), $a_0,\ldots,a_k$ are arbitrary integers such that $a_0$ is relatively prime to $b$, and $d$ is the multiplicative inverse of $-a_0$ modulo $b$. The state at step $i$ is $s_i = (x_{i-k+1},\ldots,x_{i},c_i)^{{{\sf T}}}$. In practice, the sum in (2.11) is truncated to a few terms (it could be a single term if $b$ is large), but the theoretical analysis is much easier for the infinite sum.

Define $m = \sum_{\ell=0}^k a_\ell b^\ell$ and let $a$ be the inverse of $b$ in arithmetic modulo $m$, assuming for now that $m > 0$. A major result proved in [90,11], and [24] is that if the initial states agree, the output sequence $\{u_i,\, i\ge 0\}$ is exactly the same as that produced by the LCG with modulus $m$ and multiplier $a$. Therefore, the MWC can be seen as a clever way of implementing a LCG with very large modulus. It has been shown by [11] that the value of $\ell_t$ for this LCG satisfies $\ell_t^2 \le a_0^2 + \cdots + a_k^2$ for $t\ge k$, which means that the lattice structure will be bad unless the sum of squares of coefficients $a_j$ is large.

In the original proposals of [73], called add-with-carry and subtract-with-borrow, one has $-a_0 = \pm a_r = \pm a_k = 1$ for some $r<k$ and the other coefficients $a_j$ are zero, so $\ell_t^2 \le 3$ for $t\ge k$ and the generator has essentially the same structural defect as the additive lagged-Fibonacci generator. In the version studied by [11], it was assumed that $-a_0 = d = 1$. Then, the period length cannot exceed $(m-1)/2$ if $b$ is a power of two. A concrete implementation was given in that paper. [24] pointed out that the maximal period length of $\rho = m-1$ can be achieved by allowing a more general $a_0$. They provided specific parameters that give a maximal period for $b$ ranging from $2^{21}$ to $2^{35}$ and $\rho$ up to approximately $2^{{2521}}$.