It seems natural to exploit the fact that computers work in binary
arithmetic and to design RNGs defined directly in terms of bit strings
and sequences. We do this under the following framework, taken from
[54]. Let
![]() denote the finite field with two
elements, 0 and
denote the finite field with two
elements, 0 and ![]() , in which the operations are equivalent to
addition and multiplication modulo
, in which the operations are equivalent to
addition and multiplication modulo ![]() .
Consider the RNG defined by a matrix linear recurrence over
.
Consider the RNG defined by a matrix linear recurrence over
![]() ,
as follows:
,
as follows:
It is well-known ([80,36]) that when the
![]() 's
obey (2.12), for each
's
obey (2.12), for each ![]() , the sequence
, the sequence
![]() follows the linear recurrence
follows the linear recurrence
To jump ahead directly from
![]() to
to
![]() with this
type of generator, it suffices to precompute the matrix
with this
type of generator, it suffices to precompute the matrix
![]() (in
(in
![]() ) and then multiply
) and then multiply
![]() by this matrix.
by this matrix.
Several popular classes of RNGs fit this framework as special cases,
by appropriate choices of the matrices
![]() and
and
![]() . This includes
the Tausworthe or LFSR, polynomial LCG, GFSR, twisted GFSR, Mersenne
twister, multiple recursive matrix generators, and combinations of
these ([54,78,81,88]). We detail some of them
after discussing measures of their uniformity.
. This includes
the Tausworthe or LFSR, polynomial LCG, GFSR, twisted GFSR, Mersenne
twister, multiple recursive matrix generators, and combinations of
these ([54,78,81,88]). We detail some of them
after discussing measures of their uniformity.
The uniformity of point sets ![]() produced by RNGs based on linear
recurrences over
produced by RNGs based on linear
recurrences over
![]() is usually assessed by measures of
equidistribution defined as follows
([38,54,45,88]).
For an arbitrary vector
is usually assessed by measures of
equidistribution defined as follows
([38,54,45,88]).
For an arbitrary vector
![]() of non-negative
integers, partition the unit hypercube
of non-negative
integers, partition the unit hypercube ![]() into
into ![]() intervals of the same length along axis
intervals of the same length along axis ![]() , for each
, for each ![]() . This
determines a partition of
. This
determines a partition of ![]() into
into
![]() rectangular boxes of the same size and shape. We call this partition
the
rectangular boxes of the same size and shape. We call this partition
the
![]() -equidissection of the unit hypercube.
-equidissection of the unit hypercube.
For some index set
![]() , if
, if ![]() has
has ![]() points, we say that
points, we say that ![]() is
is
![]() -equidistributed in
base
-equidistributed in
base ![]() if
there are exactly
if
there are exactly ![]() points in each box of the
points in each box of the
![]() -equidissection, where
-equidissection, where
![]() . This means
that among the
. This means
that among the ![]() points
points
![]() of
of ![]() , if
we consider the first
, if
we consider the first ![]() bits of
bits of ![]() , the first
, the first ![]() bits of
bits of
![]() , and the first
, and the first ![]() bits of
bits of ![]() , each of the
, each of the
![]() possibilities occurs exactly the same number of times. This
is possible only if
possibilities occurs exactly the same number of times. This
is possible only if ![]() .
.
The
![]() -equidistribution of
-equidistribution of ![]() depends only on the first
depends only on the first ![]() bits of
bits of ![]() for
for
![]() , for the points
, for the points
![]() that belong to
that belong to ![]() . The vector of
these
. The vector of
these
![]() bits can always be expressed as
a linear function of the
bits can always be expressed as
a linear function of the ![]() bits of the initial state
bits of the initial state
![]() , i.e.,
as
, i.e.,
as
![]() for some
for some
![]() binary matrix
binary matrix
![]() , and it is easily seen that
, and it is easily seen that ![]() is
is
![]() -equidistributed if and only if
-equidistributed if and only if
![]() has full rank
has full rank ![]() .
This provides an easy way of checking equidistribution
([22,38,88]).
.
This provides an easy way of checking equidistribution
([22,38,88]).
If ![]() is
is
![]() -equidistributed for some
-equidistributed for some ![]() , it is called
, it is called ![]() -distributed with
-distributed with ![]() bits of
accuracy, or
bits of
accuracy, or ![]() -equidistributed ([38]).
The largest value of
-equidistributed ([38]).
The largest value of ![]() for which this holds is called the
resolution of the set
for which this holds is called the
resolution of the set ![]() and is denoted by
and is denoted by ![]() .
This value has the upper bound
.
This value has the upper bound
![]() . The resolution gap of
. The resolution gap of ![]() is defined
as
is defined
as
![]() . In the same vein as for MRGs,
a worst-case figure of merit can be defined here by
. In the same vein as for MRGs,
a worst-case figure of merit can be defined here by
The point set ![]() is a
is a ![]() -net in base
-net in base ![]() (often
called a
(often
called a ![]() -net in the context of quasi-Monte Carlo
methods, where a different notation is used ([80])), if it is
-net in the context of quasi-Monte Carlo
methods, where a different notation is used ([80])), if it is
![]() -equidistributed in base
-equidistributed in base ![]() for all non-negative
integers
for all non-negative
integers
![]() summing to
summing to ![]() . We call the smallest such
. We call the smallest such
![]() the
the ![]() -value of
-value of ![]() . The smaller it is, the
better. One candidate for a figure of merit could be the
. The smaller it is, the
better. One candidate for a figure of merit could be the ![]() -value of
-value of
![]() for some large
for some large ![]() . A major drawback of this measure is that
it is extremely difficult to compute for good long-period generators
(for which
. A major drawback of this measure is that
it is extremely difficult to compute for good long-period generators
(for which ![]() is large), because there are too many vectors
is large), because there are too many vectors
![]() for which equidistribution needs to be checked. In practice, one must
settle for figures of merit that involve a smaller number of
equidissections.
for which equidistribution needs to be checked. In practice, one must
settle for figures of merit that involve a smaller number of
equidissections.
When
![]() for all sets
for all sets ![]() of the form
of the form
![]() , for
, for
![]() , the RNG is said to be
maximally equidistributed or asymptotically random
for the word size
, the RNG is said to be
maximally equidistributed or asymptotically random
for the word size ![]() ([38,88,91]).
This property ensures perfect equidistribution of all sets
([38,88,91]).
This property ensures perfect equidistribution of all sets ![]() ,
for any partition of the unit hypercube into subcubes of equal sizes,
as long as
,
for any partition of the unit hypercube into subcubes of equal sizes,
as long as ![]() and the number of subcubes does not exceed the
number of points in
and the number of subcubes does not exceed the
number of points in ![]() . Large-period maximally equidistributed
generators, together with their implementations, can be found in
[43,54], and [84], for example.
. Large-period maximally equidistributed
generators, together with their implementations, can be found in
[43,54], and [84], for example.
The RNGs defined via (2.12)-(2.14) do not have
a lattice structure in the real space like MRGs, but they do have
a lattice structure in a space of formal series, as explained in
[12,45,65], and [88]. The real space
![]() is replaced by the space
is replaced by the space
![]() of formal power series with
coefficients in
of formal power series with
coefficients in
![]() , of the form
, of the form
![]() for some integer
for some integer ![]() . In that setting, the lattices
have the form
. In that setting, the lattices
have the form
![$\displaystyle {\mathcal{L}}_t = \left\{\boldsymbol{v}(z) = \sum_{j=1}^t h_j(z) ...
...v}_j(z)\quad \text{such that each}\quad h_j(z) \in {\mathbb{F}}_2[z]\right\}\;,$](img822.gif) |
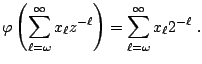 |
The Tausworthe or linear feedback shift register
(LFSR) generator ([87,38,88]) is a special case of
(2.12)-(2.14) with
![]() (in
(in
![]() ) for some
positive integer
) for some
positive integer ![]() , where
, where
| (2.17) | |
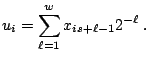 |
(2.18) |
LFSR generators can be expressed as LCGs in a space of polynomials ([89,88,36]). With this representation, their lattice structure as discussed in Sect. 2.4.3 follows immediately.
Here we take
![]() as the
as the
![]() matrix
matrix
 |
More generally, we can define
![]() as the bitwise exclusive-or
of
as the bitwise exclusive-or
of
![]() where
where ![]() , so
that each bit of
, so
that each bit of
![]() follows a recurrence in
follows a recurrence in
![]() whose
characteristic polynomial
whose
characteristic polynomial ![]() has
has ![]() nonzero terms. However,
the period length is still bounded by
nonzero terms. However,
the period length is still bounded by ![]() , whereas considering the
, whereas considering the
![]() -bit state, we should rather expect a period length close to
-bit state, we should rather expect a period length close to
![]() .
This was the main motivation for the twisted GFSR (TGFSR)
generator. In the original version introduced by [75],
.
This was the main motivation for the twisted GFSR (TGFSR)
generator. In the original version introduced by [75],
![]() and the matrix
and the matrix
![]() is defined as the transpose of
is defined as the transpose of
![]() in (2.16), with
in (2.16), with ![]() replaced by
replaced by ![]() . The characteristic
polynomial of
. The characteristic
polynomial of
![]() is then
is then
![]() , where
, where
![]() is the characteristic polynomial of
is the characteristic polynomial of ![]() ,
and its degree is
,
and its degree is ![]() . If the parameters are selected so that
. If the parameters are selected so that
![]() is primitive over
is primitive over
![]() , then the TGFSR has period
length
, then the TGFSR has period
length ![]() . [76] pointed out important weaknesses of
the original TGFSR and proposed an improved version that uses
a well-chosen matrix
. [76] pointed out important weaknesses of
the original TGFSR and proposed an improved version that uses
a well-chosen matrix
![]() whose lines differ from those of the
identity. The operations implemented by this matrix are called
tempering and their purpose is to improve the uniformity of
the points produced by the RNG.
The Mersenne twister ([78,83]) is a variant of
the TGFSR where
whose lines differ from those of the
identity. The operations implemented by this matrix are called
tempering and their purpose is to improve the uniformity of
the points produced by the RNG.
The Mersenne twister ([78,83]) is a variant of
the TGFSR where ![]() is slightly less than
is slightly less than ![]() and can be a prime
number. A specific instance proposed by [78] is fast,
robust, has the huge period length of
and can be a prime
number. A specific instance proposed by [78] is fast,
robust, has the huge period length of
![]() , and has become
quite popular.
, and has become
quite popular.
In the multiple recursive matrix method of [81],
the first row of ![]() matrices in
matrices in
![]() contains arbitrary
matrices. However, a fast implementation is possible only when these
matrices are sparse and have a special structure.
contains arbitrary
matrices. However, a fast implementation is possible only when these
matrices are sparse and have a special structure.
Many of the best generators based on linear recurrences over
![]() are constructed by combining the outputs of two or more RNGs having
a simple structure. The idea is the same as for MRGs: select simple
components that can run fast but such that their combination has
a more complicated structure and highly-uniform sets
are constructed by combining the outputs of two or more RNGs having
a simple structure. The idea is the same as for MRGs: select simple
components that can run fast but such that their combination has
a more complicated structure and highly-uniform sets ![]() for the
sets
for the
sets ![]() considered important.
considered important.
Consider ![]() distinct recurrences of the form
(2.12)-(2.13), where the
distinct recurrences of the form
(2.12)-(2.13), where the ![]() th recurrence has parameters
th recurrence has parameters
![]() and state
and state
![]() at
step
at
step ![]() , for
, for
![]() . The output of the combined generator at
step
. The output of the combined generator at
step ![]() is defined by
is defined by
With this method, by selecting the parameters carefully,
the combination of LFSR generators with characteristic polynomials
![]() gives yet another LFSR with characteristic
polynomial
gives yet another LFSR with characteristic
polynomial
![]() and period length equal
to the product of the period lengths of the components
([89,97,38,88]). Tables and fast
implementations of maximally equidistributed combined
LFSR generators are given in [38].
and period length equal
to the product of the period lengths of the components
([89,97,38,88]). Tables and fast
implementations of maximally equidistributed combined
LFSR generators are given in [38].
The TGFSR and Mersenne twister generators proposed in
[76,78] and [83] cannot be maximally
equidistributed. However, concrete examples of maximally
equidistributed combined TGFSR generators with period lengths near
![]() and
and
![]() are given in [54]. These
generators have the additional property that the resolution gaps
are given in [54]. These
generators have the additional property that the resolution gaps
![]() are zero for a class of small sets
are zero for a class of small sets ![]() with indices not too
far apart.
with indices not too
far apart.