Subsections

• 10.2.1 Single Index Models
• 10.2.2 Partially Linear Models
• 10.2.3 Nonparametric Additive Models
• 10.2.4 Transformation Models

10.2 Semiparametric Models
for Conditional Mean Functions

The term semiparametric refers to models in which there is an unknown function in addition to an unknown finite dimensional parameter. For example, the binary response model $P(Y=1\vert x)=G({\beta }'x)$ is semiparametric if the function $G$ and the vector of coefficients $\beta$ are both treated as unknown quantities. This section describes two semiparametric models of conditional mean functions that are important in applications. The section also describes a related class of models that has no unknown finite-dimensional parameters but, like semiparametric models, mitigates the disadvantages of fully nonparametric models. Finally, this section describes a class of transformation models that is important in estimation of hazard functions among other applications. Powell (1994) discusses additional semiparametric models.

10.2.1 Single Index Models

In a semiparametric single index model, the conditional mean function has the form

$$E(Y\vert x)=G({\beta }'x)\;,$$ (10.1)

where $\beta$ is an unknown constant vector and $G$ is an unknown function. The quantity ${\beta }'x$ is called an index. The inferential problem is to estimate $G$ and $\beta$ from observations of ($Y$, $X$). $G$ in (10.1) is analogous to a link function in a generalized linear model, except in (10.1) $G$ is unknown and must be estimated.

Model (10.1) contains many widely used parametric models as special cases. For example, if $G$ is the identity function, then (10.1) is a linear model. If $G$ is the cumulative normal or logistic distribution function, then (10.1) is a binary probit or logit model. When $G$ is unknown, (10.1) provides a specification that is more flexible than a parametric model but retains many of the desirable features of parametric models, as will now be explained.

One important property of single index models is that they avoid the curse of dimensionality. This is because the index ${\beta }'x$ aggregates the dimensions of $x$, thereby achieving dimension reduction. Consequently, the difference between the estimator of $G$ and the true function can be made to converge to zero at the same rate that would be achieved if ${\beta }'x$ were observable. Moreover, $\beta$ can be estimated with the same rate of convergence that is achieved in a parametric model. Thus, in terms of the rates of convergence of estimators, a single index model is as accurate as a parametric model for estimating $\beta$ and as accurate as a one-dimensional nonparametric model for estimating $G$. This dimension reduction feature of single index models gives them a considerable advantage over nonparametric methods in applications where $X$ is multidimensional and the single index structure is plausible.

A single-index model permits limited extrapolation. Specifically, it yields predictions of $E(Y\vert x)$ at values of $x$ that are not in the support of $X$ but are in the support of ${\beta }'X$. Of course, there is a price that must be paid for the ability to extrapolate. A single index model makes assumptions that are stronger than those of a nonparametric model. These assumptions are testable on the support of $X$ but not outside of it. Thus, extrapolation (unavoidably) relies on untestable assumptions about the behavior of $E(Y\vert x)$ beyond the support of $X$.

Before $\beta$ and $G$ can be estimated, restrictions must be imposed that insure their identification. That is, $\beta$ and $G$ must be uniquely determined by the population distribution of ($Y$, $X$). Identification of single index models has been investigated by Ichimura (1993) and, for the special case of binary response models, Manski (1988). It is clear that $\beta$ is not identified if $G$ is a constant function or there is an exact linear relation among the components of $X$ (perfect multicollinearity). In addition, (10.1) is observationally equivalent to the model $E(Y\vert X)=G^{\ast} (\gamma +\delta {\beta }'x)$, where $\gamma$ and $\delta \ne 0$ are arbitrary and $G^{\ast}$ is defined by the relation $G^{\ast} (\gamma +\delta v)=G(v)$ for all $v$ in the support of ${\beta }'X$. Therefore, $\beta$ and $G$ are not identified unless restrictions are imposed that uniquely specify $\gamma$ and $\delta$. The restriction on $\gamma$ is called location normalization and can be imposed by requiring $X$ to contain no constant (intercept) component. The restriction on $\delta$ is called scale normalization. Scale normalization can be achieved by setting the $\beta$ coefficient of one component of $X$ equal to one. A further identification requirement is that $X$ must include at least one continuously distributed component whose $\beta$ coefficient is non-zero. Horowitz (1998) gives an example that illustrates the need for this requirement. Other more technical identification requirements are discussed by Ichimura (1993) and Manski (1988).

The main estimation challenge in single index models is estimating $\beta$. Given an estimator $b_n$ of $\beta$, $G$ can be estimated by carrying out the nonparametric regression of $Y$ on $b_n ^{\prime} X$ (e.g, by using kernel estimation). Several estimators of $\beta$ are available. Ichimura (1993) describes a nonlinear least squares estimator. Klein and Spady (1993) describe a semiparametric maximum likelihood estimator for the case in which $Y$ is binary. These estimators are difficult to compute because they require solving complicated nonlinear optimization problems. Powell, et al. (1989) describe a density-weighted average derivative estimator (DWADE) that is non-iterative and easily computed. The DWADE applies when all components of $X$ are continuous random variables. It is based on the relation

$$\beta \propto E\left[\kern.8pt p(X)\partial G({\beta }'X)/\partial X\right] =-2E\left[Y\partial p(X)/\partial X\right]\;,$$ (10.2)

where $p$ is the probability density function of $X$ and the second equality follows from integrating the first by parts. Thus, $\beta$ can be estimated up to scale by estimating the expression on the right-hand side of the second equality. Powell, et al. (1989) show that this can be done by replacing $p$ with a nonparametric estimator and replacing the population expectation  $\boldsymbol{E}$ with a sample average. Horowitz and Härdle (1996) extend this method to models in which some components of $X$ are discrete. Hristache, Juditsky, and Spokoiny (2001) developed an iterated average derivative estimator that performs well when $X$ is high-dimensional. Ichimura and Lee (1991) and Hristache, Juditsky, Polzehl and Spokoiny (2001) investigate multiple-index generalizations of (10.1).

The usefulness of single-index models can be illustrated with an example that is taken from Horowitz and Härdle (1996). The example consists of estimating a model of product innovation by German manufacturers of investment goods. The data, assembled in 1989 by the IFO Institute of Munich, consist of observations on 1100 manufacturers. The dependent variable is $Y=1$ if a manufacturer realized an innovation during 1989 in a specific product category and 0 otherwise. The independent variables are the number of employees in the product category ($EMPLP$), the number of employees in the entire firm ($EMPLF$), an indicator of the firm's production capacity utilization ($CAP$), and a variable $DEM$, which is $1$ if a firm expected increasing demand in the product category and 0 otherwise. The first three independent variables are standardized so that they have units of standard deviations from their means. Scale normalization was achieved by setting $\beta _{EMPLP} =1$.

Table 10.1 shows the parameter estimates obtained using a binary probit model and the semiparametric method of Horowitz and Härdle (1996). Figure 10.2 shows a kernel estimate of ${G}'(\nu)$. There are two important differences between the semiparametric and probit estimates. First, the semiparametric estimate of $\beta _{EMPLF}$ is small and statistically nonsignificant, whereas the probit estimate is significant at the ${0.05}$ level and similar in size to $\beta _{CAP}$. Second, in the binary probit model, $G$ is a cumulative normal distribution function, so ${G}'$ is a normal density function. Figure 10.2 reveals, however, that ${G}'$ is bimodal. This bimodality suggests that the data may be a mixture of two populations. An obvious next step in the analysis of the data would be to search for variables that characterize these populations. Standard diagnostic techniques for binary probit models would provide no indication that ${G}'$ is bimodal. Thus, the semiparametric estimate has revealed an important feature of the data that could not easily be found using standard parametric methods.

Table 10.1: Estimated Coefficients (Standard Errors) for Model of Product Innovation

EMPLP	EMPLF	CAP	DEM
Semiparametric Model
1	0.032	0.346	1.732
	(0.023)	(0.078)	(0.509)
Probit Model
1	0.516	0.520	1.895
	(0.024)	(0.163)	(0.387)

Figure 10.2: Estimate of ${G}'(v)$ for model of product innovation

10.2.2 Partially Linear Models

In a partially linear model, $X$ is partitioned into two non-overlapping subvectors, $X_{1}$ and $X_{2}$. The model has the form

$$E(Y\vert x_1 ,x_2 )={\beta }'x_1 +G(x_2 )\;,$$ (10.3)

where $\beta$ is an unknown constant vector and $G$ is an unknown function. This model is distinct from the class of single index models. A single index model is not partially linear unless $G$ is a linear function. Conversely, a partially linear model is a single index model only in this case. Stock (1989, 1991) and Engle et al. (1986) illustrate the use of (10.3) in applications. Identification of $\beta$ requires the exclusion restriction that none of the components of $X_{1}$ are perfectly predictable by components of $X_{2}$. When $\beta$ is identified, it can be estimated with an $n^{-1/2}$ rate of convergence regardless of the dimensions of $X_{1}$ and $X_{2}$. Thus, the curse of dimensionality is avoided in estimating $\beta$.

An estimator of $\beta$ can be obtained by observing that (10.3) implies

$$Y-E(Y\vert x_2)={\beta }'\left[X_1 -E(X_1 \vert x_2 )\right]+U\;,$$ (10.4)

where $U$ is an unobserved random variable satisfying $E(U\vert x_1 ,x_2 )=0$. Robinson (1988) shows that under regularity conditions, $\beta$ can be estimated by applying OLS to (10.4) after replacing $E(Y\vert x_2 )$ and $E(X_1 \vert x_2 )$ with nonparametric estimators. The estimator of $\beta$, $b_n$, converges at rate $n^{-1/2}$ and is asymptotically normally distributed. $G$ can be estimated by carrying out the nonparametric regression of $Y-b_n ^{\prime} X_1$ on $X_2$. Unlike $b_n$, the estimator of $G$ suffers from the curse of dimensionality; its rate of convergence decreases as the dimension of $X_2$ increases.

10.2.3 Nonparametric Additive Models

Let $X$ have $d$ continuously distributed components that are denoted $X_{1}, \ldots, X_{d}$. In a nonparametric additive model of the conditional mean function,

$$E(Y\vert x)=\mu +f_1 (x_1 )+\ldots +f_d (x_d )\;,$$ (10.5)

where $\mu$ is a constant and $f_1 ,\ldots,f_d$ are unknown functions that satisfy a location normalization condition such as

$$\int f_k (v)w_k (v){\text{d}} v=0\;,\quad k=1,\ldots,d \;,$$ (10.6)

where $w_k$ is a non-negative weight function. An additive model is distinct from a single index model unless $E(Y\vert x)$ is a linear function of $x$. Additive and partially linear models are distinct unless $E(Y\vert x)$ is partially linear and $G$ in (10.3) is additive.

An estimator of $f_k \,(k=1,\ldots,d)$ can be obtained by observing that (10.5) and (10.6) imply

$$f_k (x_k)=\int E (Y\vert x)w_{-k} (x_{-k} ){\text{d}} x_{-k} \;,$$ (10.7)

where $x_{-k}$ is the vector consisting of all components of $x$ except the $k$'th and $w_{-k}$ is a weight function that satisfies $\int {w_{-k} (x_{-k} ){\text{d}} x_{-k} =1}$. The estimator of $f_k$ is obtained by replacing $E(Y\vert x)$ on the right-hand side of (10.7) with nonparametric estimators. Linton and Nielsen (1995) and Linton (1997) present the details of the procedure and extensions of it. Under suitable conditions, the estimator of $f_k$ converges to the true $f_k$ at rate $n^{-2/5}$ regardless of the dimension of $X$. Thus, the additive model provides dimension reduction. It also permits extrapolation of $E(Y\vert x)$ within the rectangle formed by the supports of the individual components of $X$. Mammen, Linton, and Nielsen (1999) describe a backfitting procedure that is likely to be more precise than the estimator based on (10.7) when $d$ is large. See Hastie and Tibshirani (1990) for an early discussion of backfitting.

Linton and Härdle (1996) describe a generalized additive model whose form is

$$E(Y\vert x)=G\left[\mu +f_1 (x_1 )+\ldots+f_K (x_d )\right] \;,$$ (10.8)

where $f_1 ,\ldots,f_d$ are unknown functions and $G$ is a known, strictly increasing (or decreasing) function. Horowitz (2001) describes a version of (10.8) in which $G$ is unknown. Both forms of (10.8) achieve dimension reduction. When $G$ is unknown, (10.8) nests additive and single index models and, under certain conditions, partially linear models.

Figure 10.3: Components of nonparametric, additive wage equation

The use of the nonparametric additive specification (10.5) can be illustrated by estimating the model $E(\log W\vert {EXP},$EDUC$)=\mu +f_{{EXP}} ({EXP})+f_{\text{\textit{EDUC}}} (\text{\textit{EDUC}})$, where $W$ and EXP are defined as in Sect. 10.1, and EDUC denotes years of education. The data are taken from the 1993 CPS and are for white males with $14$ or fewer years of education who work full time and live in urban areas of the North Central U.S. The results are shown in Fig 10.3. The unknown functions $f_{{EXP}}$ and $f_{\text{\textit{EDUC}}}$ are estimated by the method of Linton and Nielsen (1995) and are normalized so that $f_{{EXP}} (2)=f_{EDCU} (5)=0$. The estimates of $f_{{EXP}}$ (Fig 10.3a) and $f_{\text{\textit{EDUC}}}$ (Fig 10.3b) are nonlinear and differently shaped. Functions $f_{{EXP}}$ and $f_{\text{\textit{EDUC}}}$ with different shapes cannot be produced by a single index model, and a lengthy specification search might be needed to find a parametric model that produces the shapes shown in Fig 10.3. Some of the fluctuations of the estimates of $f_{{EXP}}$ and $f_{\text{\textit{EDUC}}}$ may be artifacts of random sampling error rather than features of $E(\log W\vert {EXP},$EDUC$)$. However, a more elaborate analysis that takes account of the effects of random sampling error rejects the hypothesis that either function is linear.

10.2.4 Transformation Models

A transformation model has the form

$$H(Y)={\beta }'X+U\;,$$ (10.9)

where $H$ is an unknown increasing function, $\beta$ is an unknown finite dimensional vector of constants, and $U$ is an unobserved random variable. It is assumed here that $U$ is statistically independent of $X$. The aim is to estimate $H$ and $\beta$. One possibility is to assume that $H$ is known up to a finite-dimensional parameter. For example, $H$ could be the Box-Cox transformation

$$H(y)= \begin{cases}(y^{\tau} -1)/\tau & \text{if}\;\;\tau >0\\ \log y & \text{if}\;\;\tau =0 \\ \end{cases}$$

where $\tau$ is an unknown parameter. Methods for estimating transformation models in which $H$ is parametric have been developed by Amemiya and Powell (1981) and Foster, et al. (2001) among others.

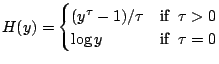Another possibility is to assume that $H$ is unknown but that the distribution of $U$ is known. Cheng, Wei, and Ying (1995, 1997) have developed estimators for this version of (10.9). Consider, first, the problem of estimating $\beta$. Let $F$ denote the (known) cumulative distribution function (CDF) of $U$. Let $(Y_i ,X_i )$ and $(Y_j ,X_j )$ $(i\ne j)$ be two distinct, independent observations of $(Y,X)$. Then it follows from (10.9) that

$$E\left[I(Y_i >Y_j )\vert X_i =x_i ,X_j =x_j \right]= P\left[U_i -U_j >-(x_i -x_j )\right]\;.$$ (10.10)

Let $G(z)=P(U_i -U_j >z)$ for any real $z$. Then

$$G(z)=\int\limits_{-\infty }^\infty \left[1-F(u+z)\right]{\text{d}} F(u) \;.$$

$G$ is a known function because $F$ is assumed known. Substituting $G$ into (10.10) gives

$$E\left[I(Y_i >Y_j )\vert X_i =x_i ,X_j =x_j \right]=G\left[-{\beta }'(x_i -x_j )\right]\;.$$

Define $X_{ij} =X_i -X_j$. Then it follows that $\beta$ satisfies the moment condition

$$E\left\{w\left({\beta }'X_{ij} \right)X_{ij} \left[I\left(Y_i >Y_j \right)-G\left(-{\beta }'X_{ij} \right)\right]\right\}=0$$ (10.11)

where $w$ is a weight function. Cheng, Wei, and Ying (1995) propose estimating $\beta$ by replacing the population moment condition (10.11) with the sample analog

$$\sum\limits_{i=1}^n \sum\limits_{j=1}^n \left\{w\left({b}'X_{ij} ... ...} \left[I\left(Y_i >Y_j \right)-G\left(-{b}'X_{ij} \right)\right]\right\} =0\;.$$ (10.12)

The estimator of $\beta$, $b_n$, is the solution to (10.12). Equation (10.12) has a unique solution if $w(z)=1$ for all $z$ and the matrix $\sum\nolimits_i \sum\nolimits_j {X}'_{ij} X_{ij}$ is positive definite. It also has a unique solution asymptotically if $w$ is positive everywhere (Cheng, Wei, and Ying 1995). Moreover, $b_n$ converges almost surely to $\beta$. Cheng, Wei, and Ying (1995) also give conditions under which $n^{1/2}(b_n -\beta )$ is asymptotically normally distributed with a mean of 0.

The problem of estimating the transformation function is addressed by Cheng, Wei, and Ying (1997). Equation (10.11) implies that for any real $y$ and vector $x$ that is conformable with $X$, $EI[I(Y\le y)\vert X=x]-F[H(y)-{\beta }'x]=0$. Cheng, Wei, and Ying (1997) propose estimating $H(y)$ by the solution to the sample analog of this equation. That is, the estimator $H_n (y)$ solves

$$n^{-1}\sum\limits_{i=1}^n \left\{ I\left(Y_i \le y\right)-F\left[H_n (y)-{b}'_n X_i \right]\right\} =0\;,$$

where $b_n$ is the solution to (10.12). Cheng, Wei, and Ying (1997) show that if $F$ is strictly increasing on its support, then $H_n (y)$ converges to $H(y)$ almost surely uniformly over any interval $[0,t]$ such that $P(Y>t)>0$. Moreover, $n^{1/2}(H_n -H)$ converges to a mean-zero Gaussian process over this interval.

A third possibility is to assume that $H$ and $F$ are both nonparametric in (10.9). In this case, certain normalizations are needed to make identification of (10.9) possible. First, observe that (10.9) continues to hold if $H$ is replaced by $cH$, $\beta$ is replaced by $c\beta$, and $U$ is replaced by $cU$ for any positive constant $c$. Therefore, a scale normalization is needed to make identification possible. This will be done here by setting $\vert \beta _1 \vert =1$, where $\beta_1$ is the first component of $\beta$. Observe, also, that when $H$ and $F$ are nonparametric, (10.9) is a semiparametric single-index model. Therefore, identification of $\beta$ requires $X$ to have at least one component whose distribution conditional on the others is continuous and whose $\beta$ coefficient is non-zero. Assume without loss of generality that the components of $X$ are ordered so that the first satisfies this condition.

It can also be seen that (10.9) is unchanged if $H$ is replaced by $H+d$ and $U$ is replaced by $U+d$ for any positive or negative constant $d$. Therefore, a location normalization is also needed to achieve identification when and $F$ are nonparametric. Location normalization will be carried out here by assuming that $H(y_0 )=0$ for some finite $y_0$ With this location normalization, there is no centering assumption on $U$ and no intercept term in $X$.

Now consider the problem of estimating $H$, $\beta$, and $F$. Because (10.9) is a single-index model in this case, $\beta$ can be estimated using the methods described in Sect. 10.2.1. Let $b_n$ denote the estimator of $\beta$. One approach to estimating $H$ and $F$ is given by Horowitz (1996). To describe this approach, define $Z={\beta }'X$. Let $G(\cdot \vert z)$ denote the CDF of $Y$ conditional on $Z=z$. Set $G_y (y\vert z)=\partial G(y\vert z)/\partial z$ and $G_z (y\vert z)=\partial G(y\vert z)/\partial z$. Then it follows from (10.9) that ${H}'(y)=-G_y (y\vert z)/G_z (y\vert z)$ and that

$$H(y)=-\int\limits_{y_0 }^y \left[G_y (v\vert z)/G_z (v\vert z)\right]{\text{d}} v$$ (10.13)

for any $z$ such that the denominator of the integrand is non-zero. Now let $w(\cdot )$ be a scalar-valued, non-negative weight function with compact support $S_w$ such that the denominator of $G_z (v\vert z)$ is bounded away from 0 for all $v\in [y_0 ,y]$ and $z\in S_w$. Also assume that

$$\int\limits_{S_w } w(z){\text{d}} z =1\;.$$

Then

$$H(y)=-\int\limits_{y_0 }^y \int\limits_{S_w } w(z)\left[G_y (v\vert z)/G_z (v\vert z)\right]{\text{d}} z\,{\text{d}} v\;.$$ (10.14)

Horowitz (1996) obtains an estimator of $H$ from (10.14) by replacing $G_y$ and $G_z$ by kernel estimators. Specifically, $G_y$ is replaced by a kernel estimator of the probability density function of $Y$ conditional on ${b}'_n X=z$, and $G_z$ is replaced by a kernel estimator of the derivative with respect to $z$ of the CDF of $Y$ conditional on ${b}'_n X=z$. Denote these estimators by $G_{ny}$ and $G_{nz}$. Then the estimator of $H$ is

$$H_n (y)=-\int\limits_{y_0 }^y \int\limits_{S_w } w(z)\left[G_{ny} (v\vert z)/G_{nz} (v\vert z)\right]{\text{d}} z\,{\text{d}} v\;.$$ (10.15)

Horowitz (1996) gives conditions under which $H_n$ is uniformly consistent for $H$ and $n^{1/2}(H_n -H)$ converges weakly to a mean-zero Gaussian process. Horowitz (1996) also shows how to estimate $F$, the CDF of $U$, and gives conditions under which $n^{1/2}(F_n -F)$ converges to a mean-zero Gaussian process, where $F_n$ is the estimator. Gørgens and Horowitz (1999) extend these results to a censored version of (10.9). Integration over $z$ in (10.14) and (10.15) accelerates the convergence of $H_n$ to $H$. Kernel estimators converge in probability at rates slower than $n^{-1/2}$. Therefore, $G_{ny} (v\vert z)/G_{nz} (v\vert z)$ is not $n^{-1/2}$-consistent for $G_y (v\vert z)/G_z (v\vert z)$. However, integration over $z$ and $v$ in (10.15) creates an averaging effect that causes the integral and, therefore, $H_n$ to converge at the rate $n^{-1/2}$. This is the reason for basing the estimator on (10.14) instead of (10.13).

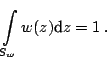Other estimators of $H$ when and $F$ are both nonparametric have been proposed by Ye and Duan (1997) and Chen (2002). Chen uses a rank-based approach that is in some ways simpler than that of Horowitz (1996) and may have better finite-sample performance. To describe this approach, define $d_{iy} =I(Y_i >y)$ and $d_{jy_0 } =I(Y_j >y_0 )$. Let $i\ne j$. Then $E(d_{iy} -d_{jy0} \vert X_i ,X_j )\ge 0$ whenever $Z_i -Z_j \ge H(y)$. This suggests that if $\beta$ were known, then $H(y)$ could be estimated by

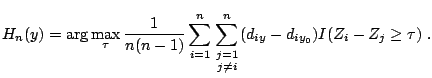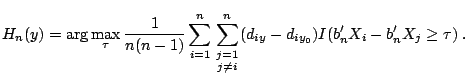$$H_n (y)=\arg \max\limits_{\tau} \frac{1}{n(n-1)} \sum\limits_{i=1... ...frac{}{}{0pt}{1}{j=1}{j\ne i}} ^n (d_{iy} -d_{iy_0 } )I(Z_i -Z_j \ge \tau )\; .$$

Since $\beta$ is unknown, Chen (2002) proposes

$$H_n (y)=\arg \max\limits_{\tau} \frac{1}{n(n-1)} \sum\limits_{i=1... ...1}{j=1}{j\ne i}} ^n (d_{iy} -d_{iy_0 } )I({b}'_n X_i -{b}'_n X_j \ge \tau )\; .$$

Chen (2002) gives conditions under which $H_n$ is uniformly consistent for $H$ and $n^{1/2}(H_n -H)$ converges to a mean-zero Gaussian process. Chen (2002) also shows how this method can be extended to a censored version of (10.9).