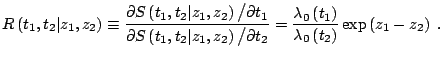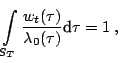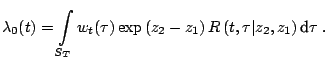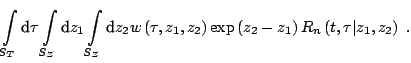



Next: 10.4 A Binary Response
Up: 10. Semiparametric Models
Previous: 10.2 Semiparametric Models for
10.3 The Proportional Hazards Model
with Unobserved Heterogeneity
Let 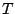 denote a duration such as that of a spell of employment or
unemployment.
Let
denote a duration such as that of a spell of employment or
unemployment.
Let
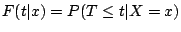 where
where 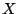 is a vector of covariates. Let
is a vector of covariates. Let
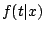 denote
the corresponding conditional probability density function. The
conditional hazard function is defined as
denote
the corresponding conditional probability density function. The
conditional hazard function is defined as
This section is concerned with an approach to modeling
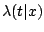 that is based on the proportional hazards model of Cox
(1972).
that is based on the proportional hazards model of Cox
(1972).
The proportional hazards model is widely used for the analysis of
duration data. Its form is
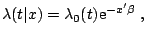 |
(10.16) |
where 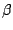 is a vector of constant parameters that is conformable
with
is a vector of constant parameters that is conformable
with 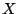 and
and
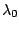 is a non-negative function that is called
the baseline hazard function. The essential characteristic of
(10.16) that distinguishes it from other models is that
is a non-negative function that is called
the baseline hazard function. The essential characteristic of
(10.16) that distinguishes it from other models is that
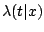 is the product of a function of
is the product of a function of 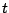 alone and
a function of
alone and
a function of 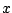 alone. Cox (1972) developed a partial likelihood
estimator of
alone. Cox (1972) developed a partial likelihood
estimator of 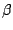 and a nonparametric estimator of
and a nonparametric estimator of
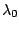 . Tsiatis (1981) derived the asymptotic properties of these
estimators.
. Tsiatis (1981) derived the asymptotic properties of these
estimators.
In the proportional hazards model with unobserved heterogeneity, the
hazard function is conditioned on the covariates 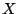 and an unobserved
random variable
and an unobserved
random variable 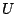 that is assumed to be independent of
that is assumed to be independent of 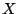 . The form
of the model is
. The form
of the model is
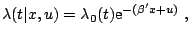 |
(10.17) |
where
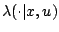 is the hazard conditional on
is the hazard conditional on
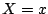 and
and 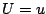 . In a model of the duration of employment
. In a model of the duration of employment 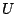 might represent unobserved attributes of an individual (possibly
ability) that affect employment duration. A variety of estimators
of
might represent unobserved attributes of an individual (possibly
ability) that affect employment duration. A variety of estimators
of 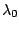 and
and 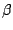 have been proposed under the assumption
that
have been proposed under the assumption
that
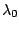 or the distribution of
or the distribution of 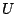 or both are known up
to a finite-dimensional parameter. See, for example, Lancaster
(1979), Heckman and Singer (1984a), Meyer (1990), Nielsen,
et al. (1992), and Murphy (1994, 1995).
However,
or both are known up
to a finite-dimensional parameter. See, for example, Lancaster
(1979), Heckman and Singer (1984a), Meyer (1990), Nielsen,
et al. (1992), and Murphy (1994, 1995).
However,
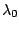 and the
distribution of
and the
distribution of 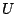 are nonparametrically identified (Elbers and
Ridder 1982, Heckman and Singer 1984b), which suggests that they
can be estimated nonparametrically.
are nonparametrically identified (Elbers and
Ridder 1982, Heckman and Singer 1984b), which suggests that they
can be estimated nonparametrically.
Horowitz (1999) describes a nonparametric estimator of
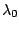 and the density of
and the density of 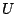 in model (10.2). His estimator is
based on expressing (10.2) as a type of transformation
model. To do this, define the integrated baseline hazard funtion,
in model (10.2). His estimator is
based on expressing (10.2) as a type of transformation
model. To do this, define the integrated baseline hazard funtion,
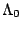 by
by
Then it is not difficult to show that (10.2) is equivalent
to the transformation model
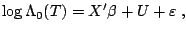 |
(10.18) |
where
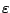 is a random variable that is independent of
is a random variable that is independent of 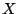 and
and 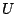 and has the CDF
and has the CDF
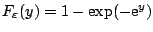 . Now define
. Now define
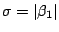 , where
, where 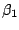 is the first
component of
is the first
component of 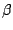 and is assumed to be non-zero. Then
and is assumed to be non-zero. Then
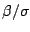 and
and
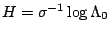 can be estimated by
using the methods of Sect. 10.2.4. Denote the
resulting estimators of
can be estimated by
using the methods of Sect. 10.2.4. Denote the
resulting estimators of
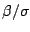 and
and 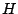 by
by 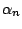 and
and
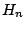 . If
. If 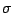 were known, then
were known, then 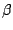 and
and
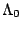 could
be estimated by
could
be estimated by
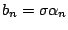 and
and
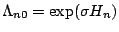 . The baseline hazard function
. The baseline hazard function
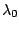 could be
estimated by differentiating
could be
estimated by differentiating
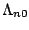 . Thus, it is necessary
only to find an estimator of the scale parameter
. Thus, it is necessary
only to find an estimator of the scale parameter 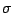 .
.
To do this, define
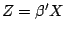 , and let
, and let
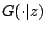 denote
the CDF of
denote
the CDF of 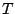 conditional on
conditional on 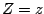 . It can be shown that
. It can be shown that
where 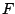 is the CDF of
is the CDF of 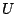 . Let
. Let 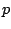 denote the probability density
function of
denote the probability density
function of 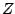 . Define
. Define
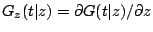 and
and
Then it can be shown using l'Hospital's rule that if
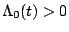 for all
for all 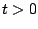 , then
, then
To estimate 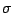 , let
, let 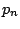 ,
, 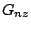 and
and 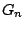 be kernel
estimators of
be kernel
estimators of 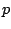 ,
, 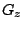 and
and 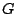 , respectively, that are based on
a simple random sample of
, respectively, that are based on
a simple random sample of 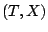 . Define
. Define
Let 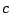 ,
, 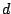 , and
, and 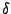 be constants satisfying
be constants satisfying
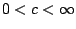 ,
,
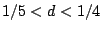 , and
, and
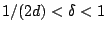 . Let
. Let
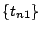 and
and
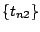 be sequences of positive numbers such that
be sequences of positive numbers such that
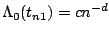 and
and
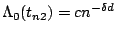 . Then
. Then 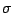 is estimated consistently by
is estimated consistently by
Horowitz (1999) gives conditions under which
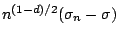 is asymptotically normally distributed with a mean of
zero. By choosing
is asymptotically normally distributed with a mean of
zero. By choosing 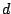 to be close to
to be close to 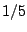 , the rate of convergence in
probability of
, the rate of convergence in
probability of 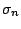 to
to 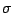 can be made arbitrarily close
to
can be made arbitrarily close
to 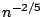 , which is the fastest possible rate (Ishwaran 1996). It
follows from an application of the delta method that the estimators of
, which is the fastest possible rate (Ishwaran 1996). It
follows from an application of the delta method that the estimators of
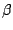 ,
,
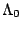 , and
, and
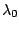 that are given by
that are given by
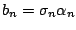 ,
,
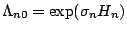 , and
, and
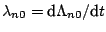 are also asymptotically
normally distributed with means of zero and
are also asymptotically
normally distributed with means of zero and
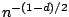 rates of
convergence. The probability density function of
rates of
convergence. The probability density function of 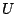 can be estimated
consistently by solving the deconvolution problem
can be estimated
consistently by solving the deconvolution problem
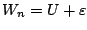 , where
, where
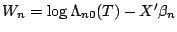 . Because the
distribution of
. Because the
distribution of
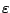 is ''supersmooth,'' the resulting
rate of convergence of the estimator of the density of
is ''supersmooth,'' the resulting
rate of convergence of the estimator of the density of 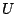 is
is
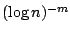 , where
, where 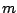 is the number of times that the density is
differentiable. This is the fastest possible rate. Horowitz (1999)
also shows how to obtain data-based values for
is the number of times that the density is
differentiable. This is the fastest possible rate. Horowitz (1999)
also shows how to obtain data-based values for 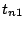 and
and 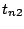 and extends the estimation method to models with censoring.
and extends the estimation method to models with censoring.
If panel data on 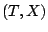 are available, then
are available, then
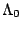 can be
estimated with a
can be
estimated with a 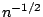 rate of convergence, and the assumption of
independence of
rate of convergence, and the assumption of
independence of 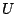 from
from 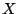 can be dropped. Suppose that each
individual in a random sample of individuals is observed for exactly
two spells. Let
can be dropped. Suppose that each
individual in a random sample of individuals is observed for exactly
two spells. Let
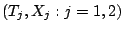 denote the values of
denote the values of 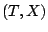 in
the two spells. Define
in
the two spells. Define
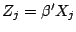 . Then the joint survivor
function of
. Then the joint survivor
function of 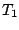 and
and 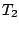 conditional on
conditional on 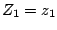 and
and 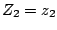 is
is
Honoré(1993) showed that
Adopt the scale normalization
where 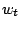 is a non-negative weight function and
is a non-negative weight function and 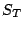 is its
support. Then
is its
support. Then
Now for a weight function 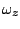 with support
with support 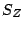 , define
, define
Then,
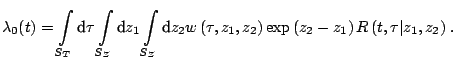 |
(10.19) |
The baseline hazard function can now be estimated by replacing 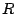 with an estimator,
with an estimator, 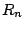 , in (10.19). This can be done by
replacing
, in (10.19). This can be done by
replacing 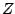 with
with 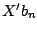 , where
, where 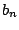 is a consistent estimator
of
is a consistent estimator
of 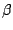 such as a marginal likelihood estimator (Chamberlain 1985,
Kalbfleisch and Prentice 1980, Lancaster 2000, Ridder and Tunali
1999), and replacing
such as a marginal likelihood estimator (Chamberlain 1985,
Kalbfleisch and Prentice 1980, Lancaster 2000, Ridder and Tunali
1999), and replacing 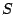 with a kernel estimator of the joint survivor
function conditional
with a kernel estimator of the joint survivor
function conditional
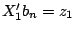 and
and
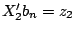 . The
resulting estimator of
. The
resulting estimator of
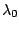 is
is
The integrated baseline hazard function is estimated by
Horowitz and Lee (2004) give conditions under which
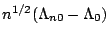 converges weakly to a tight, mean-zero Gaussian
process. The estimated baseline hazard function
converges weakly to a tight, mean-zero Gaussian
process. The estimated baseline hazard function
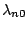 converges at the rate
converges at the rate
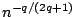 , where
, where 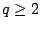 is the number of
times that
is the number of
times that
 is continuously differentiable. Horowitz and
Lee (2004) also show how to estimate a censored version of the model.
is continuously differentiable. Horowitz and
Lee (2004) also show how to estimate a censored version of the model.




Next: 10.4 A Binary Response
Up: 10. Semiparametric Models
Previous: 10.2 Semiparametric Models for
![]() denote a duration such as that of a spell of employment or
unemployment.
Let
denote a duration such as that of a spell of employment or
unemployment.
Let
![]() where
where ![]() is a vector of covariates. Let
is a vector of covariates. Let
![]() denote
the corresponding conditional probability density function. The
conditional hazard function is defined as
denote
the corresponding conditional probability density function. The
conditional hazard function is defined as
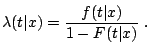
![]() and an unobserved
random variable
and an unobserved
random variable ![]() that is assumed to be independent of
that is assumed to be independent of ![]() . The form
of the model is
. The form
of the model is
![]() and the density of
and the density of ![]() in model (10.2). His estimator is
based on expressing (10.2) as a type of transformation
model. To do this, define the integrated baseline hazard funtion,
in model (10.2). His estimator is
based on expressing (10.2) as a type of transformation
model. To do this, define the integrated baseline hazard funtion,
![]() by
by
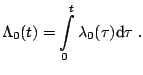
![]() , and let
, and let
![]() denote
the CDF of
denote
the CDF of ![]() conditional on
conditional on ![]() . It can be shown that
. It can be shown that
![$\displaystyle G(t\vert z)=1-\int \exp \left[-\Lambda _0 (t)\mathrm{e}^{-({\beta }'x+u)}\right]{\text{d}} F(u)\;,$](img6009.gif)
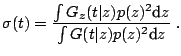
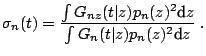
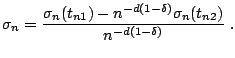
![]() are available, then
are available, then
![]() can be
estimated with a
can be
estimated with a ![]() rate of convergence, and the assumption of
independence of
rate of convergence, and the assumption of
independence of ![]() from
from ![]() can be dropped. Suppose that each
individual in a random sample of individuals is observed for exactly
two spells. Let
can be dropped. Suppose that each
individual in a random sample of individuals is observed for exactly
two spells. Let
![]() denote the values of
denote the values of ![]() in
the two spells. Define
in
the two spells. Define
![]() . Then the joint survivor
function of
. Then the joint survivor
function of ![]() and
and ![]() conditional on
conditional on ![]() and
and ![]() is
is
![$\displaystyle =\int {\exp \left[-\Lambda _0 \left(t_1 \right)\mathrm{e}^{z_1 +u...
...athrm{e}^{z_2 +u}\right]{\text{d}} P\left(u\vert Z_1 =z_1 ,Z_2 =z_2 \right)}\;.$](img6046.gif)