10.4 A Binary Response Model

The general binary response model has the form

$$Y=I({\beta }'X+U>0)\;,$$ (10.20)

where $U$ is an unobserved random variable. If the distribution of $U$ is unknown but depends on $X$ only through the index ${\beta }'X$, then (10.20) is a single-index model, and $\beta$ can be estimated by the methods described in Sect. 10.2.1. An alternative model that is non-nested with single-index models can be obtained by assuming that median$(U\vert X=x)=0$ for all $x$. This assumption places only weak restrictions on the relation between $X$ and the distribution of $U$. Among other things, it accommodates fairly general types of heteroskedasticity of unknown form, including random coefficients. Under median centering, the inferential problem is to estimate $\beta$. The response function, $P(Y=1\vert X=x)$ is not identified without making assumptions about the distribution of $U$ that are stronger than those needed to identify and estimate $\beta$. Without such assumptions, the only restriction on $P(Y=1\vert X=x)$ under median centering is that

$$P(Y=1\vert X=x) \begin{cases}>{0.5}&\text{if}\;\;{\beta }'x>0 \\ ={0.5}&\text{if}\;\;{\beta }'x=0 \\ <{0.5}&\text{if}\;\;{\beta }'x<0 \end{cases}$$

Manski (1975, 1985) proposed the first estimator of $\beta$ under median centering. Let the data be the simple random sample $\{Y_i ,X_i :\;i=1,\ldots,n\}$. The estimator is called the maximum score estimator and is

$$b_n =\arg \max\limits_{\left\Vert b \right\Vert=1} n^{-1}\sum\limits_{i=1}^n {(2Y_i -1)I({b}'X_i \ge 0)} \;,$$ (10.21)

where $\left\Vert b \right\Vert$ denotes the Euclidean norm of the vector $b$. The restriction $\left\Vert b \right\Vert=1$ is a scale normalization. Scale normalization is needed for identification because (10.20) identifies $\beta$ only up to scale. Manski (1975, 1985) gave conditions under which $b_n$ consistently estimates $\beta$. The rate of convergence of $b_n$ and its asymptotic distribution were derived by Cavanagh (1987) and Kim and Pollard (1990). They showed that the rate of convergence in probability of $b_n$ to $\beta$ is $n^{-1/3}$ and that $n^{1/3}(b_n -\beta )$ converges in distribution to the maximum of a complicated multidimensional stochastic process. The complexity of the limiting distribution of the maximum score estimator limits its usefulness for statistical inference. Delgado, Rodríguez-Póo and Wolf (2001) proposed using subsampling methods to form confidence intervals for $\beta$.

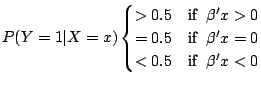The maximum score estimator has a slow rate of convergence and a complicated asymptotic distribution because it is obtained by maximizing a step function. Horowitz (1992) proposed replacing the indicator function in (10.21) by a smooth function. The resulting estimator of $\beta$ is called the smoothed maximum score estimator. Specifically, let $K$ be a smooth function, possibly but not necessarily a distribution function, that satisfies $K(-\infty )=0$ and $K(\infty )=1$. Let $\{h_n :\;n=1,2,\ldots\}$ be a sequence of strictly positive constants (bandwidths) that satisfies $h_n \to 0$ as $n\to\infty$. The smoothed maximum score estimator, $b_{ns}$, is

$$b_{ns} =\arg \max\limits_{b\in B} \sum\limits_{i=1}^n {(2Y_i -1)K({X}'_i b/h_n )} \;,$$

where $B$ is a compact parameter set that satisfies the scale normalization $\vert b_1 \vert =1$. Horowitz (1992) shows that under assumptions that are stronger than those of Manski (1975, 1985) but still quite weak, $n^r(b_{ns} -\beta )$ is asymptotically normal, where $2/5\le r<1/2$ and the exact value of $r$ depends on the smoothness of the distribution of ${X}'\beta$ and of $P(Y=1\vert X=x)$. Moreover, the smoothed maximum score estimator has the fastest possible rate of convergence under its assumptions (Horowitz 1993b). Monte Carlo evidence suggests that the asymptotic normal approximation can be inaccurate with samples of practical size. However, Horowitz (2002) shows that the bootstrap, which is implemented by sampling the data randomly with replacement, provides asymptotic refinements for tests of hypotheses about $\beta$ and produces low ERPs for these tests. Thus, the bootstrap provides a practical way to carry out inference with the smoothed maximum score estimator.

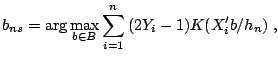Horowitz (1993c) used the smoothed maximum score method to estimate the parameters of a model of the choice between automobile and transit for work trips in the Washington, D.C., area. The explanatory variables are defined in Table 10.2. Scale normalization is achieved by setting the coefficient of DCOST equal to $1$. The data consist of 842 observations sampled randomly from the Washington, D.C., area transportation study. Each record contains information about a single trip to work, including the chosen mode (automobile or transit) and the values of the explanatory variables. Column 2 of Table 10.2 shows the smoothed maximum score estimates of the model's parameters. Column 3 shows the half-widths of nominal ${90}\,\%$ symmetrical confidence intervals based on the asymptotic normal approximation (half width equals ${1.67}$ times the standard error of the estimate). Column 4 shows half-widths obtained from the bootstrap. The bootstrap confidence intervals are ${2.5}$-$3$ times wider than the intervals based on the asymptotic normal approximation. The bootstrap confidence interval for the coefficient of DOVTT contains 0, but the confidence interval based on the asymptotic normal approximation does not. Therefore, the hypothesis that the coefficient of DOVTT is zero is not rejected at the $0.1$ level based on the bootstrap but is rejected based on the asymptotic normal approximation.

Table 10.2: Smoothed Maximum Score Estimates of a Work-Trip Mode-Choice Model

		Half-Width of Nominal ${90}\,\%$
		Conf. Interval Based on
	Estimated	Asymp. Normal
Variable $^{\text{a}}$	Coefficient	Approximation	Bootstrap
INTRCPT	-1.5761	0.2812	0.7664
AUTOS	2.2418	0.2989	0.7488
DOVTT	0.0269	0.0124	0.0310
DIVTT	0.0143	0.0033	0.0087
DCOST	1.0 $^{\text{b}}$

$^{\text{a}}$ Definitions of variables: INTRCPT: Intercept term equal to $1$; AUTOS: Number of cars owned by traveler's household; DOVTT: Transit out-of-vehicle travel time minus automobile out-of-vehicle travel time (minutes); DIVTT: Transit in-vehicle travel time minus automobile in-vehicle travel time; DCOST: Transit fare minus automobile travel cost ($).
$^{\text{b}}$ Coefficient equal to 1 by scale normalization

Acknowledgements. Research supported in part by NSF Grant SES-9910925.