Let ![]() be a positive random variable with density function
be a positive random variable with density function
![]() and distribution function
and distribution function ![]() . The survival function
. The survival function
![]() is then defined as
is then defined as
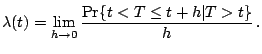 |
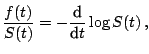 |
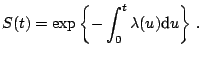 |
(12.2) |
We assume that the observed data set consists of failure or
death times ![]() and censoring indicators
and censoring indicators ![]() ,
,
![]() . The indicator
. The indicator ![]() is unity for the case of
failure and zero for censoring. The censoring scheme is an
important concept in survival analysis in that one can observe
partial information associated with the survival random
variable. This is due to some limitations such as loss to
follow-up, drop-out, termination of the study, and others.
is unity for the case of
failure and zero for censoring. The censoring scheme is an
important concept in survival analysis in that one can observe
partial information associated with the survival random
variable. This is due to some limitations such as loss to
follow-up, drop-out, termination of the study, and others.
The Kaplan-Meier method ([18]) is currently the standard for estimating the nonparametric survival function. For the case of a sample without any censoring observations, the estimate exactly corresponds to the derivation from the empirical distribution. The dataset can be arranged in table form, i.e.,
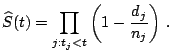 |
(12.3) |
SE![$\displaystyle \left\{\widehat{S}(t)\right\} = \left[\widehat{S}(t)\right]\left\{\sum _{j:t_j<t} \frac{d_j}{n_j(n_j-d_j)} \right\}^{1/2}\,.$](img6469.gif) |
(12.4) |
The most important and widely-used models in survival analysis are exponential, Weibull, log-normal, log-logistic, and gamma distributions. The first two models will be introduced for later consideration. The exponential distribution is simplistic and easy to handle, being similar to a standard distribution in some respects, while the Weibull distribution is a generalization of the exponential distribution and allows inclusion of many types of shapes. Their density functions are
| (12.5) | ||
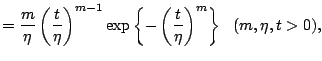 |
(12.6) |
As the Weibull distribution completely includes the exponential distribution, only the Weibull model will be discussed further. The Weibull distribution is widely used in reliability and biomedical engineering because of goodness of fit to data and ease of handling. The main objective in lifetime analysis sometimes involves (1) estimation of a few parameters which define the Weibull distribution, and (2) evaluation of the effects of some environmental factors on lifetime distribution using regression techniques. Inference on the quantiles of the distribution has been previously studied in detail ([14]).
The maximum likelihood estimate (MLE) is well known, yet it is not expressed
explicitly in closed form. Accordingly, some iterative
computational methods are used. Menon ([21])
provided a simple estimator of ![]() , being a consistent
estimate of
, being a consistent
estimate of ![]() , with a bias that tends to vanish as the
sample size increases. Later, Cohen ([3,4])
presented a practically useful chart for obtaining a good
first approximation to the shape parameter
, with a bias that tends to vanish as the
sample size increases. Later, Cohen ([3,4])
presented a practically useful chart for obtaining a good
first approximation to the shape parameter ![]() using the property that the coefficient of
variation of the Weibull
distribution is a function of the shape parameter
using the property that the coefficient of
variation of the Weibull
distribution is a function of the shape parameter ![]() , i.e.,
it does not depend on
, i.e.,
it does not depend on ![]() . This is described as follows.
. This is described as follows.
Let ![]() be a random variable with probability density function
(12.6), the
be a random variable with probability density function
(12.6), the ![]() th moment around the
origin is then calculated as
th moment around the
origin is then calculated as
![$\displaystyle \notag E[T]=\eta\Gamma\left(1+\frac{1}{m}\right)\,,$](img6479.gif) |
![$\displaystyle \notag {\text{Var}}[T]=\eta^2\left\{\Gamma\left(1+\frac{2}{m}\right)-\Gamma^2\left(1+\frac{1}{m}\right)\right\}\,.$](img6480.gif) |
Regarding the three-parameter Weibull described by
(
![]() ), [4] suggested using
the method of moments equations,
noting that
), [4] suggested using
the method of moments equations,
noting that
As for obtaining an inference on the parameter of the mean
parameter ![]() , this has not yet been investigated and
will now be discussed. When one would like to estimate
, this has not yet been investigated and
will now be discussed. When one would like to estimate ![]() ,
use of either the MLE or the standard sample mean is best for
considering the case of an unknown shape parameter. This is
true because the asymptotic relative
efficiency of the sample
mean to the MLE is calculated as
,
use of either the MLE or the standard sample mean is best for
considering the case of an unknown shape parameter. This is
true because the asymptotic relative
efficiency of the sample
mean to the MLE is calculated as
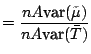 |
||
![$\displaystyle = \frac{6}{m^2\pi^2}\cdot\frac{1}{{\text{CV}}^2}\left[ \frac{\pi^2}{6}+\left\{c-1+\psi(1+1/m)\right\}^2\right]\,,\,$](img6494.gif) |
(12.8) |
Table 12.2 gives the ARE with respect to
various values of ![]() . Note the remarkably high efficiency of
the sample mean,
especially for
. Note the remarkably high efficiency of
the sample mean,
especially for ![]() , where more than
, where more than ![]() efficiency is indicated. The behavior of
efficiency is indicated. The behavior of
![]() form
form ![]() is that
is that
![]() has a local minimum 0.9979 at
has a local minimum 0.9979 at
![]() and a local maximum 0.9986 at
and a local maximum 0.9986 at ![]() , and that
for the larger
, and that
for the larger ![]() ,
,
![]() monotonically
decreases in
monotonically
decreases in ![]() and the infimum of
and the infimum of
![]() is
given in
is
given in
![]() ;
;
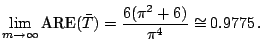 |
(12.9) |
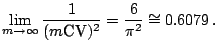 |
(12.10) |
| eff | eff | eff | |||
| 0.1 | 0.0018 | 1.1 | 0.9997 | 2.1 | 0.9980 |
| 0.2 | 0.1993 | 1.2 | 0.9993 | 2.2 | 0.9981 |
| 0.3 | 0.5771 | 1.3 | 0.9988 | 2.3 | 0.9982 |
| 0.4 | 0.8119 | 1.4 | 0.9984 | 2.4 | 0.9983 |
| 0.5 | 0.9216 | 1.5 | 0.9981 | 2.5 | 0.9984 |
| 0.6 | 0.9691 | 1.6 | 0.9980 | 2.6 | 0.9984 |
| 0.7 | 0.9890 | 1.7 | 0.9979 | 2.7 | 0.9985 |
| 0.8 | 0.9968 | 1.8 | 0.9979 | 2.8 | 0.9985 |
| 0.9 | 0.9995 | 1.9 | 0.9979 | 2.9 | 0.9985 |
| 1.0 | 1.0000 | 2.0 | 0.9980 | 3.0 | 0.9986 |