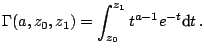



Next: 12.3 Regression Models
Up: 12. Computational Methods in
Previous: 12.1 Introduction
Let us now consider the class of the lifetime distributions,
whose distribution functions are expressed by
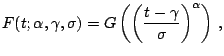 |
(12.11) |
where 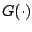 is also a distribution function. For the
Weibull model,
is also a distribution function. For the
Weibull model,
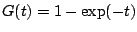 is an exponential
distribution. Nagatsuka and Kamakura
([24], [25]) proposed a new method using
the location-scale-free
transformation of
data set to estimate the power parameter in the Castillo-Hadi model ([2]). That is, let
is an exponential
distribution. Nagatsuka and Kamakura
([24], [25]) proposed a new method using
the location-scale-free
transformation of
data set to estimate the power parameter in the Castillo-Hadi model ([2]). That is, let
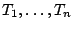 be
independently distributed according to the distribution
function (12.11). Consider the
be
independently distributed according to the distribution
function (12.11). Consider the
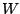 -transformation to be defined as
-transformation to be defined as
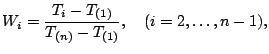 |
(12.12) |
where 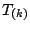 is the
is the 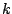 -th order statistic of
-th order statistic of 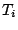 's. The
new random variables
's. The
new random variables 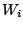 's derived by this
's derived by this 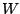 -transformation
are then free from location and scale parameter. The
arithmetic mean of
-transformation
are then free from location and scale parameter. The
arithmetic mean of 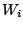 's gives the approximation to the
original distribution of
's gives the approximation to the
original distribution of 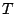 . Let
. Let
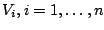 be
i.i.d. distributed with common distribution function
be
i.i.d. distributed with common distribution function 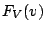 ,
and let the
,
and let the 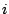 -th order statistic
-th order statistic 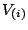 have the marginal
distribution function
have the marginal
distribution function
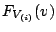 . Then
. Then
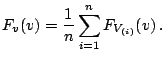 |
(12.13) |
This equation indicates that the arithmetic mean of the
marginal distributions of 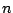 order statistics is exactly the
original distribution. In the case of the Castillo-Hadi Model,
[25] provided a theorem regarding this
approximation, i.e.,
order statistics is exactly the
original distribution. In the case of the Castillo-Hadi Model,
[25] provided a theorem regarding this
approximation, i.e.,
Theorem 1 ([
25])
The mixture of the marginal distributions of 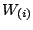 ,
,
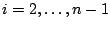 :
:
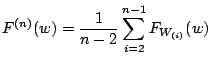 |
(12.14) |
is the approximate distribution of 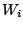 's and the limiting
distribution (12.14) is the power function
distribution with parameter
's and the limiting
distribution (12.14) is the power function
distribution with parameter 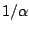 . That is
. That is
In the case of the Weibull distribution, the marginal
distribution of 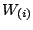 is calculated as
is calculated as
where
Calculations show that
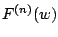 has a first moment of
has a first moment of
where
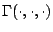 is the incomplete
generalized gamma function defined by
is the incomplete
generalized gamma function defined by
Now, an estimating of the shape parameter 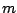 is obtained by
equating the theoretical population mean with sample mean of
is obtained by
equating the theoretical population mean with sample mean of
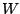 -transformed
-transformed 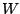 's. [24] provided a table for
obtaining estimates and concluded based on simulation studies
that the robust estimate of
's. [24] provided a table for
obtaining estimates and concluded based on simulation studies
that the robust estimate of 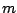 is possible without using any
existing threshold parameter.
is possible without using any
existing threshold parameter.




Next: 12.3 Regression Models
Up: 12. Computational Methods in
Previous: 12.1 Introduction
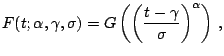
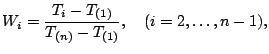
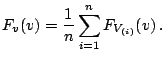
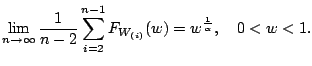
![]() is calculated as
is calculated as
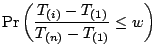
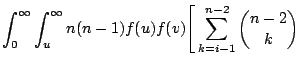
![$\displaystyle \times \left\{F(v)-F((1-w)u+wv)\right\}^{n-k-2} \Bigg]{\text{d}}v{\text{d}}u$](img6529.gif)
![$\displaystyle \int _0^1\int _u^1 n(n-1)\sum _{k=i-1}^{n-2}\binom{n-2}{k} \times\left[1-\exp\left\{-\alpha(w,m,u,v)\right\}-u\right]^k$](img6530.gif)
![]() has a first moment of
has a first moment of