The standard methods of survival analysis can be generalized to include multiple failures simply defined as a series of well-defined event occurrences. For example, in software reliability, engineers are often interested in detecting software bugs. Inference from a single counting process has been studied in detail ([8,23]), with multiple independent processes being considered as a means to estimate a common cumulative mean function from a nonparametric or semi-parametric viewpoint ([20,26]). [16] discussed problems associated with parametric conditional inference in models with a common trend parameter or possibly different base-line intensity parameters.
For multiple failures, intensity functions correspond to hazard functions in that the intensity function is defined as discussed next.
In time interval ![]() we define the number of occurrences
of events or failures as
we define the number of occurrences
of events or failures as ![]() . The Poisson counting process
. The Poisson counting process
![]() is given such that it satisfies the
following three conditions for
is given such that it satisfies the
following three conditions for ![]() .
.
For this counting process
![]() we can define
the intensity function as
we can define
the intensity function as
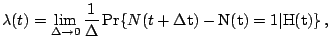 |
(12.26) |
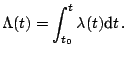 |
![$\displaystyle E[N_{s,t}]=\sum_{n=0}^\infty n \Pr \{N_{n,s}=n\}=\Lambda_t - \Lambda_s\,,$](img6640.gif) |
(12.27) |
![$\displaystyle \lambda (t) = \frac{{\text{d}}}{{\text{d}}t}\Lambda_t = \frac{{\text{d}}}{{\text{d}}t}E[N(t)]\,.$](img6641.gif) |
(12.28) |
The nonparametric estimate of the intensity function is easy to determine and is quite useful for observing the trend of a series of events. If a data set of failure times
![]() is available, assuming constant intensity in
is available, assuming constant intensity in
![]() , then
, then
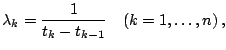 |
(12.29) |
We assume several independent counting
processes
![]() , i.e.,
, i.e.,
![]() . The cumulative mean function for
. The cumulative mean function for
![]() is expressed by
is expressed by
| (12.30) |
[26] described a method for estimating the cumulative mean function of an identically distributed process without assuming any Poisson process structure, while [20] developed robust variance estimates based on the Poisson process. All these methods are basically concerned with nonparametric estimation. Here, parametric models for effectively acquiring information on the trend of an event occurrence are dealt with. [16] considered generalized versions of two primal parametric models to multiple independent counting processes under the framework of a nonhomogeneous Poisson process.
Cox and Lewis ([8]) considered a log-linear model for trend testing a singe counting process, i.e.,
| (12.31) |
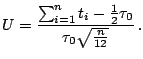 |
(12.32) |
The distribution of this statistic steeply converges to the
standard normal distribution when
![]() . This
statistic is sometimes called the
. This
statistic is sometimes called the ![]() statistic and is
frequently applied to trend testing in reliability
engineering.
statistic and is
frequently applied to trend testing in reliability
engineering.
[16] generalized this log-linear model to the
multiple case, with the log-linear model for ![]() -th individual
being
-th individual
being
| (12.33) |
In this modeling we assume the common trend parameter ![]() and are mainly interested in estimating and testing this
parameter. The full likelihood for the model becomes
and are mainly interested in estimating and testing this
parameter. The full likelihood for the model becomes
![$\displaystyle = \prod _{k=1}^K \left[\left\{\prod _{i=1}^{n_k}\lambda _k(t_{ki})\right\}\exp\left\{ -\int _0^{\tau _k}\lambda _k (u) {\text{d}}u\right\}\right]$](img6657.gif) |
(12.34) | |
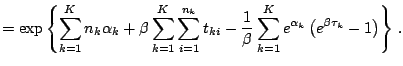 |
Given
![]() , conditional
likelihood is considered as
, conditional
likelihood is considered as
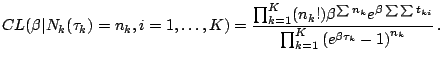 |
(12.35) |
![$\displaystyle = E\left[-\frac{ \partial^2 \log CL } {\partial \beta ^2 } \right]$](img6662.gif) |
||
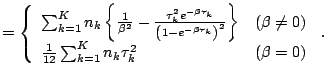 |
(12.36) |
The test statistic obtained from the above calculations becomes
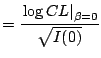 |
||
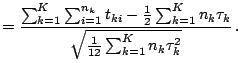 |
(12.37) |
To obtain the conditional estimate, numerical calculations are
required such as Newton-Raphson method. However, the log conditional likelihood and its
derivatives are not computable at the origin of the parameter
![]() . In such a case, Taylor series expansions of the log conditional likelihood are used
around the origin ([16]).
. In such a case, Taylor series expansions of the log conditional likelihood are used
around the origin ([16]).
[9] considered the power law model, sometimes
called the Weibull process model.
This model was generalized to the multiple case using the
following intensity for the ![]() -th individual
([16]):
-th individual
([16]):
| (12.38) |
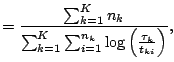 |
(12.39) | |
| (12.40) |
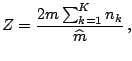 |
(12.41) |
Estimation based on conditional likelihood allows effectively eliminating the nuisance
parameter and obtaining information
on the structure parameter. Let us
now consider the class of nonhomogeneous Poisson
process models which are
specified by the intensity parameterized by two
parameters. The first parameter ![]() is concerned with the
base line occurrences for the individual, while the second
parameter
is concerned with the
base line occurrences for the individual, while the second
parameter ![]() is concerned with the trend of
intensity. For simplicity, the property of the intensity for
is concerned with the trend of
intensity. For simplicity, the property of the intensity for
![]() is examined. Using conditional likelihood is convenient
because the nuisance parameter
is examined. Using conditional likelihood is convenient
because the nuisance parameter ![]() need not be known.
This is of great importance in multiple intensity modeling,
i.e.,
need not be known.
This is of great importance in multiple intensity modeling,
i.e.,
| (12.42) |
Several intensity models for software reliability are described in [23]: the log-linear model, geometric model, inverse linear model, inverse polynomial model, and power law model, all of which are included in this class satisfying the condition of the theorem.
Acknowledgements. This work has been partially supported financially by Chuo University as one of the 2003 Research Projects for Promotion of Advanced Research at Graduate School.