We have highlighted some applications of decision trees. Here, we will explain how they are constructed. There has been a surge of interest lately in using decision trees to identify genes underlying complex diseases. For this reason, we will begin the explanation of the basic idea with a genomic example, and then will also discuss other examples.
[81] analyzed a data set from the expression profiles of
![]() genes in
genes in ![]() normal and
normal and ![]() colon cancer tissues
([2]). In this data set, the response
colon cancer tissues
([2]). In this data set, the response ![]() equals 0 or
equals 0 or ![]() according to whether the tissue is normal or with cancer. Each element
of
according to whether the tissue is normal or with cancer. Each element
of
![]() is the expression profile for one of the
is the expression profile for one of the
![]() genes. The objective is to identify genes and to use them
to construct a tree so that we can classify the tumor type according
to the selected gene expression profiles. Figure 14.1 is
a classification tree constructed from this data set. In what follows,
we will explain how such a tree is constructed and how it can be
interpreted.
genes. The objective is to identify genes and to use them
to construct a tree so that we can classify the tumor type according
to the selected gene expression profiles. Figure 14.1 is
a classification tree constructed from this data set. In what follows,
we will explain how such a tree is constructed and how it can be
interpreted.
Tree construction usually comprises two steps: growing and
pruning. The growing step begins with the root node, which is the
entire learning sample. In the present example, the root node
contains the ![]() tissues and it is labeled as node
tissues and it is labeled as node ![]() on the top of
Fig. 14.1. The most fundamental step in tree growing
is to partition the root node into two subgroups, referred to as
daughter nodes,
such that one daughter node contains mostly cancer tissue and the
other daughter node mostly normal tissue. Such a partition is chosen
from all possible binary splits based on the
on the top of
Fig. 14.1. The most fundamental step in tree growing
is to partition the root node into two subgroups, referred to as
daughter nodes,
such that one daughter node contains mostly cancer tissue and the
other daughter node mostly normal tissue. Such a partition is chosen
from all possible binary splits based on the ![]() gene
expression profiles via questions like ''Is the expression level of
gene
gene
expression profiles via questions like ''Is the expression level of
gene ![]() greater than
greater than ![]() ?'' A tissue is assigned to the right or
left daughter according to whether the answer is yes or no. When all
of the
?'' A tissue is assigned to the right or
left daughter according to whether the answer is yes or no. When all
of the ![]() tissues are assigned to either the left or right daughter
nodes, the distribution in terms of the number of cancer tissues is
assessed for both the left and right nodes using typically a node
impurity.
One of such criteria is the entropy
function
tissues are assigned to either the left or right daughter
nodes, the distribution in terms of the number of cancer tissues is
assessed for both the left and right nodes using typically a node
impurity.
One of such criteria is the entropy
function
Let L and R denote the left and right nodes, respectively. The quality
of the split ![]() , resulting from the question ''Is the expression
level of gene
, resulting from the question ''Is the expression
level of gene ![]() greater than
greater than ![]() ?'' is measured by weighing
?'' is measured by weighing
![]() and
and
![]() as follows:
as follows:
The objective of the tree growing step is to produce a tree by executing the recursive partitioning process as far as possible. A natural concern is that such a saturated tree is generally too big and prone to noise. This calls for the second step to prune the saturated tree in order to obtain a reasonably sized tree that is still discriminative of the response whereas parsimonious for interpretation and robust with respect to the noise.
For the purpose of tree pruning,
[6] introduced misclassification cost
to penalize the errors of classification such as classifying a cancer
tissue as a normal one, and vice versa. The unit of misclassification
cost is chosen to reflect the seriousness of the errors because the
consequence of classifying a cancer tissue as a normal one is usually
more severe than classifying a normal tissue as a cancer one. A common
practice is to assign a unit cost for classifying a normal tissue as
a cancer one and a cost, ![]() , for classifying a cancer tissue as
a normal one. Once
, for classifying a cancer tissue as
a normal one. Once ![]() is chosen, the class membership for any node
can be determined to minimize the misclassification cost. For example,
the root node of Fig. 14.1 is classified as a cancer node
for any
is chosen, the class membership for any node
can be determined to minimize the misclassification cost. For example,
the root node of Fig. 14.1 is classified as a cancer node
for any ![]() chosen to be greater than
chosen to be greater than ![]() . While
. While ![]() is
usually chosen to be greater than
is
usually chosen to be greater than ![]() , for the purpose of illustration
here, if it is chosen to be 0.5, the root node is classified as
a normal node because it gives rise to a lower misclassification cost.
, for the purpose of illustration
here, if it is chosen to be 0.5, the root node is classified as
a normal node because it gives rise to a lower misclassification cost.
When the class memberships and misclassification costs are determined
for all nodes, the misclassification cost for a tree can be computed
easily by summing all costs in the terminal nodes. A node is terminal
when it is not further divided, and other nodes are referred to as
internal nodes. Precisely, the quality of a tree, denoted by ![]() , is
reflected by the quality of its terminal nodes as follows:
, is
reflected by the quality of its terminal nodes as follows:
The ultimate objective of tree pruning is to select a subtree of the
saturated tree so that the misclassification cost of the selected
subtree is the lowest on an independent, identically distributed
sample, called a test sample.
In practice, we rarely have a test sample. [6] proposed
to use cross validation
based on cost-complexity.
They defined the number of the terminal nodes
of ![]() , denoted by
, denoted by
![]() , as the complexity of
, as the complexity of ![]() .
A penalizing cost, the so-called complexity parameter,
is assigned to one unit increase in complexity, i.e., one extra
terminal node. The sum of all costs becomes the penalty for the tree
complexity, and the cost-complexity of a tree is:
.
A penalizing cost, the so-called complexity parameter,
is assigned to one unit increase in complexity, i.e., one extra
terminal node. The sum of all costs becomes the penalty for the tree
complexity, and the cost-complexity of a tree is:
A useful and interesting result from [6] is that, for
a given complexity parameter, there is a unique smallest subtree of
the saturated tree that minimizes the cost-complexity
measure (14.3). Furthermore, if
![]() the
optimally pruned subtree corresponding to
the
optimally pruned subtree corresponding to ![]() is a subtree of
the one corresponding to
is a subtree of
the one corresponding to ![]() . Therefore, increasing the
complexity parameter produces a finite sequence of nested optimally
pruned subtrees, which makes the selection of the desirably-sized
subtree feasible.
. Therefore, increasing the
complexity parameter produces a finite sequence of nested optimally
pruned subtrees, which makes the selection of the desirably-sized
subtree feasible.
Although the introduction of misclassification cost and cost complexity provides a solution to tree pruning, it is usually a subjective and difficult decision to choose the misclassification costs for different errors. Moreover, the final tree can be heavily dependent on such a subjective choice. From a methodological point of view, generalizing the concept of misclassification cost is difficult when we have to deal with more complicated responses, which we will discuss in detail later. For these reasons, we prefer a simpler way for pruning as described by [63] and [79].
Let us now return to the example. In Fig. 14.1, the
![]() tissues are divided into four terminal nodes
tissues are divided into four terminal nodes ![]() ,
, ![]() ,
, ![]() ,
and
,
and ![]() . Two of them (Nodes
. Two of them (Nodes ![]() and
and ![]() ) contain
) contain ![]() normal tissues
and no cancer tissue. The other two nodes (Node
normal tissues
and no cancer tissue. The other two nodes (Node ![]() and
and ![]() ) contain
) contain
![]() cancer tissues and
cancer tissues and ![]() normal tissue. Because this tree is
relatively small and has nearly perfect classification, pruning is
almost unnecessary. Interestingly, this is not accidental for analyses
of many microarray data for which there are many genes and relatively
few samples.
normal tissue. Because this tree is
relatively small and has nearly perfect classification, pruning is
almost unnecessary. Interestingly, this is not accidental for analyses
of many microarray data for which there are many genes and relatively
few samples.
The construction of Fig. 14.1 follows the growing
procedure as described above. First, node ![]() is split into nodes
is split into nodes ![]() and
and ![]() after examining all allowable splits from the
after examining all allowable splits from the ![]() gene
expression profiles, and the expression level of gene IL-8 and its
threshold at
gene
expression profiles, and the expression level of gene IL-8 and its
threshold at ![]() are chosen because they result in the lowest
weighted impurity of nodes
are chosen because they result in the lowest
weighted impurity of nodes ![]() and
and ![]() . A tissue is sent to the left
(node
. A tissue is sent to the left
(node ![]() ) or right (node
) or right (node ![]() ) daughter node according to whether or
not the IL-8 level is below
) daughter node according to whether or
not the IL-8 level is below ![]() . Because node
. Because node ![]() is pure, no further
split is necessary and it becomes a terminal node. Node
is pure, no further
split is necessary and it becomes a terminal node. Node ![]() is split
into nodes
is split
into nodes ![]() and
and ![]() through recursive partitioning and according to
whether or not the expression of gene CANX is greater than
through recursive partitioning and according to
whether or not the expression of gene CANX is greater than ![]() ,
while the partition is restricted to the
,
while the partition is restricted to the ![]() tissues in node
tissues in node ![]() only. Furthermore, node
only. Furthermore, node ![]() is subsequently partitioned into
nodes
is subsequently partitioned into
nodes ![]() and
and ![]() according to whether or not the expression of gene
RAB3B exceeds
according to whether or not the expression of gene
RAB3B exceeds ![]() .
.
There are also many interesting applications of simple classification
trees. For example, [35] used classification trees to
predict heart attack based on information from ![]() patients. After
a tree is constructed, the prediction is made from a series of
questions such as ''Is the pain in the neck only?'' and/or ''Is
the pain in the neck and shoulder?'' An appealing feature of tree-based
classification is that the classification rule is based on the answers
to simple and intuitive questions as posed here.
patients. After
a tree is constructed, the prediction is made from a series of
questions such as ''Is the pain in the neck only?'' and/or ''Is
the pain in the neck and shoulder?'' An appealing feature of tree-based
classification is that the classification rule is based on the answers
to simple and intuitive questions as posed here.
Although we present classification trees for a binary response, the method is similar for a mult-level response. The impurity function can be defined as
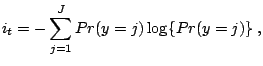 |