



Next: 14.4 Interpretation
Up: 14. Recursive Partitioning and
Previous: 14.2 Basic Classification Trees
Subsections
14.3 Computational Issues
In Sects. 14.2.1 and 14.2.2, we have explained the
basic steps and concepts for tree construction. For most users of
decision trees, the implementation aspect does not really affect the
application. For methodological and software developments, however, it
is imperative to understand the computational issues. The most
critical issue is to find the optimal split efficiently for any given
node. The overall strategy is to identify the optimal split from each
of the predictors and then choose the overall best one. Choosing the
overall best one is straightforward, but identifying the optimal split
from a predictor takes some efforts. The algorithm must take into
account the nature of the predictor. Although we will use
a dichotomous response to explain the ideas, the algorithm is also
applicable for the other types of responses.
14.3.1 Splits Based on an Ordinal Predictor
Let us first consider a predictor with an ordinal scale such as gene
expression in Fig. 14.1 or the ratio of cash flow to
total debt in Fig. 14.2. Under the tree framework, as
long as a predictor is ordinal, we will soon see that it does not
matter whether the predictor is on a continuous or discrete scale.
Table 14.1:
Expression level of gene IL-8 in 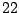 normal and
normal and 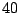 colon cancer tissues
used in Fig. 14.1
colon cancer tissues
used in Fig. 14.1
| Expression |
Colon |
Expression |
Colon |
Expression |
Colon |
Expression |
Colon |
| level |
cancer |
level |
cancer |
level |
cancer |
level |
cancer |
| 23.74 |
N |
35.95875 |
N |
33.9725 |
N |
45.1 |
N |
| 56.91875 |
N |
28.7675 |
N |
28.00875 |
N |
39.7575 |
N |
| 11.37625 |
N |
31.6975 |
N |
30.57875 |
N |
171.4525 |
N |
| 36.8675 |
N |
40.33875 |
N |
76.9875 |
N |
97.92 |
N |
| 55.2 |
N |
238.58625 |
N |
645.99375 |
N |
117.6025 |
N |
| 113.91375 |
N |
567.13125 |
N |
1528.4062 |
Y |
306.30875 |
Y |
| 76.125 |
Y |
169.1375 |
Y |
213.6275 |
Y |
326.42625 |
Y |
| 370.04 |
Y |
114.92375 |
Y |
311.4375 |
Y |
186.2775 |
Y |
| 131.65875 |
Y |
412.135 |
Y |
284.14625 |
Y |
1178.9188 |
Y |
| 75.81375 |
Y |
1007.5262 |
Y |
120.72 |
Y |
227.70625 |
Y |
| 80.73875 |
Y |
2076.9025 |
Y |
93.3575 |
Y |
1813.4562 |
Y |
| 170.11875 |
Y |
737.695 |
Y |
270.19625 |
Y |
75.95 |
Y |
| 62.7375 |
Y |
148.04125 |
Y |
599.6975 |
Y |
247.52625 |
Y |
| 390.31125 |
Y |
222.55875 |
Y |
391.355 |
Y |
249.15125 |
Y |
| 117.185 |
Y |
104.78125 |
Y |
124.91875 |
Y |
210.90125 |
Y |
| 519.08125 |
Y |
175.55125 |
Y |
|
|
|
|
Table 14.1 displays the expression levels of gene IL-8 in
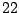 normal and
normal and  colon cancer tissues. Our objective for the time
being is to split these
colon cancer tissues. Our objective for the time
being is to split these  tissues into two subsamples according to
whether the expression level of gene IL-8 is greater than a given
threshold. In theory, this threshold can be anything, but practically,
there is only a finite number of them that make a difference. In other
words, it takes a finite number of steps to find an optimal threshold,
although the solution is not unique.
tissues into two subsamples according to
whether the expression level of gene IL-8 is greater than a given
threshold. In theory, this threshold can be anything, but practically,
there is only a finite number of them that make a difference. In other
words, it takes a finite number of steps to find an optimal threshold,
although the solution is not unique.
Table 14.2:
Sorted expression level of gene IL-8 in  normal and
normal and  colon
cancer tissues used in Fig. 14.1
colon
cancer tissues used in Fig. 14.1
| Expression |
Colon |
Expression |
Colon |
Expression |
Colon |
Expression |
Colon |
| level |
cancer |
level |
cancer |
level |
cancer |
level |
cancer |
| 11.37625 |
N |
23.74 |
N |
28.00875 |
N |
28.7675 |
N |
| 30.57875 |
N |
31.6975 |
N |
33.9725 |
N |
35.95875 |
N |
| 36.8675 |
N |
39.7575 |
N |
40.33875 |
N |
45.1 |
N |
| 55.2 |
N |
56.91875 |
N |
62.7375 |
Y |
75.81375 |
Y |
| 75.95 |
Y |
76.125 |
Y |
76.9875 |
N |
80.73875 |
Y |
| 93.3575 |
Y |
97.92 |
N |
104.78125 |
Y |
113.91375 |
N |
| 114.92375 |
Y |
117.185 |
Y |
117.6025 |
N |
120.72 |
Y |
| 124.91875 |
Y |
131.65875 |
Y |
148.04125 |
Y |
169.1375 |
Y |
| 170.11875 |
Y |
171.4525 |
N |
175.55125 |
Y |
186.2775 |
Y |
| 210.90125 |
Y |
213.6275 |
Y |
222.55875 |
Y |
227.70625 |
Y |
| 238.58625 |
N |
247.52625 |
Y |
249.15125 |
Y |
270.19625 |
Y |
| 284.14625 |
Y |
645.99375 |
N |
306.30875 |
Y |
311.4375 |
Y |
| 326.42625 |
Y |
370.04 |
Y |
390.31125 |
Y |
391.355 |
Y |
| 412.135 |
Y |
519.08125 |
Y |
567.13125 |
N |
599.6975 |
Y |
| 737.695 |
Y |
1007.5262 |
Y |
1178.9188 |
Y |
1528.4062 |
Y |
| 1813.4562 |
Y |
2076.9025 |
Y |
|
|
|
|
The first step in finding an optimal threshold is to sort all
expression levels, say, in an ascending order as displayed in
Table 14.2. If the threshold is below the minimum
(11.37625) or above the maximum (2076.9025), it produces
an empty subsample. Thus, the threshold should be between
11.37625 and 2076.9025. If we take a look at the two
lowest levels, 11.37625 and 23.74, it is clear that any
threshold between these two levels produces the same two subsamples
(or daughter nodes). In this example, there are 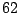 distinct levels
of expression. Thus, we have
distinct levels
of expression. Thus, we have 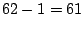 distinct ways to split the
distinct ways to split the
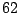 samples into two daughter nodes. It is noteworthy that, unlike
this example, the number of unique levels of a predictor is usually
lower than the number of samples.
samples into two daughter nodes. It is noteworthy that, unlike
this example, the number of unique levels of a predictor is usually
lower than the number of samples.
The second step in finding an optimal threshold is to move along the
intervals defined by two adjacent, distinct levels of the sorted
predictor values. In Table 14.2, we move along as
follows:
For computation, the threshold can be chosen as the middle point of
the above intervals. For interpretation, the threshold can be
rounded-off as is done to the first split in Fig. 14.1.
We have determined the pool of the potential thresholds, which is
sometimes referred to as the allowable splits.
Obviously, we can examine each threshold one at a time and assess its
quality according to (14.1).
Table 14.3:
Search for the optimal split
| |
Left node |
Right node |
Split |
| |
No. of |
No. of |
Node |
No. of |
No. of |
Node |
Quality |
| Interval |
sample |
cancer |
impurity |
sample |
cancer |
impurity |
 |
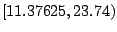 |
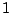 |
0 |
0 |
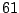 |
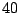 |
0.6438 |
0.3666 |
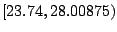 |
 |
0 |
0 |
 |
 |
0.6365 |
0.3849 |
 |
 |
 |
 |
 |
 |
 |
 |
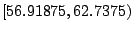 |
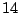 |
0 |
0 |
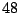 |
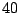 |
0.4506 |
0.6512 |
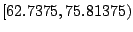 |
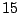 |
 |
0.1030 |
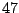 |
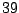 |
0.4562 |
0.6292 |
 |
 |
 |
 |
 |
 |
 |
 |
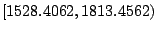 |
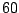 |
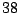 |
0.6572 |
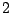 |
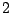 |
0 |
0.3640 |
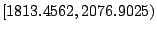 |
 |
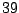 |
0.6538 |
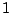 |
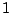 |
0 |
0.3568 |
For a large data set, this means a lot of wasted computing time. To
reduce the computation to a minimal level, let us take a careful look
as to what happens when we move the threshold from one interval to the
next. In Table 14.3, as the threshold is moved up to the
next interval, the samples that were already assigned to the left
daughter stay on the left side because their expression levels are
still below the new threshold. Most of the samples that were assigned
to the right daughter stay on the right side, except those samples
whose expression levels are equal to the lower limit of the new
interval. In this particular case, there is only one sample that we
need to move from the right side to the left every time we move the
threshold by one interval. This observation implies that the node
impurities and the split quality can be computed by updating the
information slightly for the small set of the samples that are
affected. Every of such a small set of samples is affected only once
in the entire search of the predictor. In summary, after the values of
a predictor are sorted, we can find an optimal threshold to split
a node in the number of steps proportional to the number of distinct
values of the predictor, which is at most the number of samples in the
node. For the present example, any value in
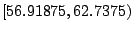 is an optimal split. Intuitively from
Table 14.3, we push the threshold as high as possible to
maintain the perfect purity of the left daughter node. In the
meantime, if we look bottom-up from the table, we also push the
threshold as low as possible to maximize the purity of the right
daughter node. The interval
is an optimal split. Intuitively from
Table 14.3, we push the threshold as high as possible to
maintain the perfect purity of the left daughter node. In the
meantime, if we look bottom-up from the table, we also push the
threshold as low as possible to maximize the purity of the right
daughter node. The interval
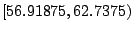 offers
the best balance. In Fig. 14.1, the split is chosen
at
offers
the best balance. In Fig. 14.1, the split is chosen
at 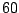 , although any number in this interval is a legitimate choice.
, although any number in this interval is a legitimate choice.
Overall, if we have 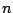 samples in a node and
samples in a node and 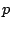 predictors,
excluding the sorting time, the final threshold for the node can be
identified in at most
predictors,
excluding the sorting time, the final threshold for the node can be
identified in at most 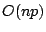 steps.
steps.
For a nominal variable, we cannot sort the values of the variable as
we did in Table 14.2. For a predictor of 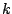 levels,
there are a total of
levels,
there are a total of 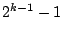 ways to split a node. To explain the
algorithm, let us use an artificial example as summarized in
Table 14.4.
ways to split a node. To explain the
algorithm, let us use an artificial example as summarized in
Table 14.4.
Table 14.4:
An artificial data set
| Predictor |
No. of |
No. of |
Rate of |
| value |
normal |
cancer |
cancer |
| A |
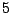 |
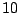 |
0.67 |
| B |
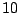 |
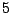 |
0.33 |
| C |
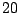 |
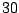 |
0.60 |
| D |
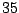 |
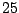 |
0.42 |
In Table 14.4, the predictor has 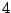 levels, giving rise
to
levels, giving rise
to 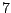 possible ways to split a node. A naive way is to assess every
allowable split on an individual basis. This could be an extensive
computation when the number of levels is
possible ways to split a node. A naive way is to assess every
allowable split on an individual basis. This could be an extensive
computation when the number of levels is 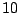 or higher. Thus, it is
important to find a way to compute the quality of all splits in
a gradual manner as in Sect. 14.3.1. If we focus on the
levels of the predictor for the left daughter node, we can travel all
or higher. Thus, it is
important to find a way to compute the quality of all splits in
a gradual manner as in Sect. 14.3.1. If we focus on the
levels of the predictor for the left daughter node, we can travel all
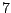 possible splits as follows:
possible splits as follows: 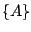 ,
, 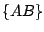 ,
, 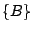 ,
, 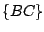 ,
,
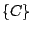 ,
, 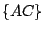 , and
, and 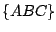 . The key is that every move requires
either the deletion or addition of a single level, which keeps the
computation at the minimal level. Such a path of traveling through all
. The key is that every move requires
either the deletion or addition of a single level, which keeps the
computation at the minimal level. Such a path of traveling through all
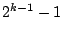 splits can be defined for any
splits can be defined for any 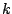 .
.
There is actually a simple and quick solution for a dichotomous
response. As shown in Table 14.4, we can compute the
cancer rate for every level of the nominal predictor. During the
splitting, the rates can substitute for the corresponding nominal
levels. Because the rates are ordinal, the method described in
Sect. 14.3.1 can be applied. After the optimal split is
determined, we can map the rate back to the original nominal
level. For example, for the data in Table 14.4, the
optimal threshold based on the rate is in the interval
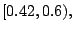 which means that the left daughter node contains samples
with levels B and D, and the right daughter node with levels A
and C. For a multiclass response, there is no apparent way to form an
ordinal surrogate for a nominal predictor.
which means that the left daughter node contains samples
with levels B and D, and the right daughter node with levels A
and C. For a multiclass response, there is no apparent way to form an
ordinal surrogate for a nominal predictor.
An important feature of decision trees is their ability to deal with
missing predictor values. There are several solutions. Although there
have been limited attempts ([62]) to compare some of
them, the performance of the various solutions is largely
unexplored. The choice mostly depends on the objective of the study.
The easiest approach is to treat the missing attribute as a distinct
value and to assign all samples with missing values to the same node
([78]). This approach is not only simple, but also
provides clear paths as to where the samples with missing attributes
end up in the tree structure.
[6] introduced and advocated surrogate splits
to deal with missing attributes. The idea is very intuitive. For
example, in Table 14.2, we considered using expression
levels from gene IL-8 to split the  samples. What happens if the
expression level from one of the samples, say, the first one, was not
recorded? This happens in microarray experiments. Because IL-8 level
is missing for the first sample, we cannot determine whether the level
is below or above
samples. What happens if the
expression level from one of the samples, say, the first one, was not
recorded? This happens in microarray experiments. Because IL-8 level
is missing for the first sample, we cannot determine whether the level
is below or above  and hence cannot decide whether the first
sample should be assigned to the left or right daughter node. To
resolve this ambiguity, [6] proposed to seek help from
other genes that act ''similarly'' to IL-8. Since there are many
other genes, we can use the one that is most similar to IL-8, which
leads to a surrogate for IL-8.
and hence cannot decide whether the first
sample should be assigned to the left or right daughter node. To
resolve this ambiguity, [6] proposed to seek help from
other genes that act ''similarly'' to IL-8. Since there are many
other genes, we can use the one that is most similar to IL-8, which
leads to a surrogate for IL-8.
What we need to clarify is the meaning of similarity. To illustrate
this concept, let us consider gene CANX. Using the method described in
Sect. 14.3.1, we can find an optimal split from gene
CANX. The similarity between CANX and IL-8 is the probability that the
optimal splits from these two genes assign a sample with complete
information in these two genes into the same node. This strategy is
similar to replacing a missing value in one variable in linear
regression by regressing on the non-missing value most highly
correlated with it. Then, why can't we use the same strategy as in
the linear regression? According to [6], their strategy
is more robust. The main reason is that their strategy is more
specific to the particular sample with missing attributes, and does
not result in a potential catastrophic impact for other samples with
missing attributes.
The surrogate splits have some advantages over the simpler approach as
described earlier. It makes use of other potentially useful
information. [6] also proposed to rank the importance of
variables through surrogate splits. The surrogate splits also have
some limitations. First, it is uncommon, if at all, that surrogate
splits are provided in published applications. Thus, it is
unrealistic to know what the surrogate splits are and how we assign
a sample with a missing attribute. Second, there is no guarantee in
a data set that we can find a satisfactory surrogate split. Lastly,
while it is a sensible idea to rank the variable importance based on
surrogate splits, there is no assurance that a predictor ranked
relatively high is necessarily predictive of the outcome, which can
create a dilemma for interpretation. More recently, the importance of
a variable tends to be evaluated on the basis of its performance in
forests ([7,80]) rather than on a single tree.
In the construction of random forests,
Breiman proposed another way of replacing missing values through an
iterative process. A similar idea can be applied for tree
construction. To initialize the process, we can fill in the missing
values by the median of an ordered variable or by the category of
a nominal variable with the highest frequency. An initial tree can be
constructed once all missing data are imputed. In the next step,
suppose again that in Table 14.2, the expression of gene
IL-8 is missing for the first sample. The unobserved level is
estimated by a weighted average over the samples with observed
expressions for gene IL-8. Here, the weight is the so-called
proximity,
which is a similarity measure between a pair of samples. Intuitively,
if the second sample is more similar to the first sample than to the
third one, we give more weight to the second sample than to the third
one if the first sample is not observed. How is the proximity defined
for a pair of samples? We can set it to zero before the initial tree
is grown. Then, whenever a tree is grown, if two samples end up in the
same terminal nodes, its promixity is increased by one unit. After
the missing data are updated, a new tree is grown. Breiman recommends
to continue this process at most five times in the random forest
construction. For tree construction, it may take longer for the
process to ''converge'', especially when the number of predictors is
large. Nonetheless, it may still be worthwhile to repeat a few
iterations. In addition to this convergence issue, it is also
difficult to track where the samples with missing values are assigned
as with the use of surrogate splits.




Next: 14.4 Interpretation
Up: 14. Recursive Partitioning and
Previous: 14.2 Basic Classification Trees