Subsections

• 14.5.1 Maximizing Difference Between Nodes
• 14.5.2 Use of Likelihood Functions
• 14.5.3 A Straightforward Extension
• 14.5.4 Other Developments

14.5 Survival Trees

The most popular use of tree-based methods is arguably in survival analysis for censored time, particularly in biomedical applications. The general goal of such applications is to identify prognostic factors that are predictive of survival outcome and time to an event of interest. For example, [5] reported a tree-based analysis that enables the natural identification of prognostic groups among patients in the perioperative phase, using information available regarding several clinicopathologic variables. Such groupings are important because patients treated with radical prostatectomy for clinically localized prostate carcinoma present considerable heterogeneity in terms of disease-free survival outcome, and the groupings allow physicians to make early yet prudent decisions regarding adjuvant combination therapies. See, e.g., [3], [12], [13] and [44] for additional examples.

Before pointing out the methodological challenge in extending the basic classification trees to survival trees, let us quickly introduce the censored data. Let $z$ denote the time to an event, which can be death or the occurrence of a disease. For a variety of reasons including losts to follow-up and the limited period of a study, we may not be able to observe $z$ until the event occurs for everyone in the study. Thus, what we actually observe is a censored time $y$ which is smaller than or equal to $z$. When $z$ is observed, $y=z$. Otherwise, $z$ is censored and $y<z$. Let $\delta=1$ or 0 denote whether $z$ is censored or observed.

The question is how to facilitate the censored time $y$ in the tree-based methods. As in Sect. 14.2, we need to define a splitting criterion to divide a node into two, and also to find a way to choose a ''right-sized'' tree. Many authors have proposed different methods to address these needs. Here, we describe some of the methods. See [21], [43], [47], [63], [65], [77] and [79] for more details.

14.5.1 Maximizing Difference Between Nodes

[40] are among the earliest to have developed survival trees. Earlier, we focused on reducing the impurity within a node by splitting. When two daughter nodes have low impurities, the distributions of the response tend to differ between the two nodes. In other words, we could have achieved the same goal by maximizing the difference between the distributions of the response in the two daughter nodes. There are well established statistics that measure the difference in distribution. In survival analysis, we can compute the Kaplan-Meier curves (see, e.g., [52]) separately for each node. Gordon and Olshen used the so-called $L^p$ Wasserstein metrics, $d_p(\cdot, \cdot)$, as the measure of discrepancy between the two survival functions. Specifically, for $p=1$, the Wasserstein distance, $d_1(S_L, S_R)$, between two Kaplan-Meier curves, $S_L$ and $S_R$, is illustrated in Fig. 14.4.

Figure 14.4: The $L^1$ Wasserstein distance between two Kaplan-Meier curves as measured by the area marked with $d_1$. Note that one curve $(S_L)$ is thicker than the other $(S_R)$

A desirable split maximizes the distance, $d_1(S_L, S_R)$, where $S_L$ and $S_R$ are the Kaplan-Meier curves for the left and right daughter nodes, respectively. Replacing $g_s$ in (14.1) with $-d_1(S_L,S_R)$ we can split the root node into two daughter nodes and use the same recursive partitioning process as before to produce a saturated tree.

To prune a saturated survival tree, $T$, [40] generalized the tree cost-complexity for censored data. The complexity remains the same as before, but we need to redefine the cost $R(t)$, which now is measured by how far node $t$ deviates from a desirable node in lieu of a pure node in the binary response case. In the present situation, a replacement for a pure node is a node $\tau$ in which all observed times are the same, and hence its Kaplan-Meier curve, $\delta _{\tau}$, is a piecewise constant survival function that has at most one point of discontinuity. Then, the within-node cost, $R(t)$, is defined as $d_1(S_t,\delta _{\tau})$. Combining this newly defined cost-complexity with the previously described pruning step serves as a method for pruning survival trees.

Another, perhaps more commonly used way to measure the difference in survival distributions is to make use of the log-rank statistic. Indeed, the procedures proposed by [18] and [63] maximize the log-rank statistic by comparing the survival distributions between the two daughter nodes. The authors did not define the cost-complexity using the log-rank statistic. However, [46] introduced the notion of ''goodness-of-split'' complexity as a substitute for cost-complexity in pruning survival trees. Let $G(t)$ be the value of the log-rank test at node $t$. Then the split-complexity measure is

$$G(T)=\sum_{t\not\in {\widetilde{T}}}G(t)-\alpha \left(\vert\widetilde{T}\vert-1\right)\;.$$

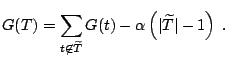[69] proposed another way to define $R(t)$ that makes use of the so-called martingale residuals by assuming within-node proportional hazard models and then the least squares are computed as the cost.

In our experience, we found that Segal's bottom-up procedure ([63]) is practical and easy to use. That is, for each internal node (including the root node) of a saturated tree, we assign it a value that equals the maximum of the log-rank statistics over all splits starting from the internal node of interest. Then, we plot the values for all internal nodes in an increasing order and decide a threshold from the graph. If an internal node corresponds to a smaller value than the threshold, we prune all of its offspring. [79] pointed out that this practical procedure can be modified in a broad context by replacing the log-rank statistic with a test statistic that is appropriate for comparing two samples with a defined outcome.

14.5.2 Use of Likelihood Functions

Although the concept of node impurity is very useful in the development of tree-based methodology, that concept is closely related to the concept of likelihood as pointed out by [77]. In fact, the adoption of likelihood makes it much easier to extend the tree-based methodology to analysis of complex dependent variables including censored time. For example, [23] assume that the survival function within any given node is an exponential function with a constant hazard. [45] and [17] assume different within-node hazard functions. Specifically, the hazard functions in two daughter nodes are assumed proportional, but are unknown. In terms of estimation, [45] use the full or partial likelihood function in the Cox proportional hazard model whereas [17] use a partial likelihood function.

The most critical idea in using the likelihood is that within-node survival functions are temporarily assumed to serve as a vehicle of finding a split instead of believing them to be the true ones. For example, we cannot have a constant hazard function in the left daughter node, and then another constant hazard function in the right daughter node while assuming that the parent node also has a constant hazard function. Here, the constant hazard function plays the role of the ''sample average''. However, after a tree is constructed, it is both reasonable and possible that the hazard functions within the terminal nodes may become approximately constant.

14.5.3 A Straightforward Extension

[73] examined a straightforward tree-based approach to censored survival data by observing the fact that the response variable involves two dimensions: a binary censoring indicator and the observed time. If we can split a node so that the node impurity is ''minimized'' in both dimensions, the within-node survival distribution is expected to be homogeneous. Based on this intuitive idea, [73] proposed to compute the within-node impurity in terms of both the censoring indicator and the observed time first separately, and then together through weighting. Empirically, this simple approach tends to produce trees similar to those produced from using the log-rank test. More interestingly, empirical evidence also suggests that this simple approach outperforms its more sophisticated counterparts in discovering the underlying structures of data. Unfortunately, there need to be more comparative studies to scrutinize these different methods, even though limited simulations comparing some of the methods have been reported in the literature ([21,22,73]).

14.5.4 Other Developments

The methods that we described above are not designed to deal with time-dependent covariates. [3] and [41] proposed similar approaches to accommodate the time-dependent covariates in survival trees. The main concern with these existing approaches is that the same subject can be assigned to both the left and right daughter nodes, which is distinct from any other tree-based methods and is potentially confusing in interpretation.

It is common in survival tree analysis that we want to stratify our sample into at a few groups that define the grades for the survival. To this end, it is useful to combine some terminal nodes into one group, which is loosely called ''amalgamation''. [18] used the log-rank statistic for this purpose. [46] proposed constructing an ordinal variable that describes the terminal nodes. Often, we can simply examine the Kaplan-Meier curves for all terminal nodes to determine the group membership ([13]).