This section covers relevant matrix decompositions and basic numerical methods. Decompositions provide a numerically stable way to solve a system of linear equations, as shown already in [65], and to invert a matrix. Additionally, they provide an important tool for analyzing the numerical stability of a system.
Some of most frequently used decompositions are the Cholesky, QR, LU, and SVD decompositions. We start with the Cholesky and LU decompositions, which work only with positive definite and nonsingular diagonally dominant square matrices, respectively (Sects. 4.1.1 and 4.1.2). Later, we explore more general and in statistics more widely used QR and SVD decompositions, which can be applied to any matrix (Sects. 4.1.3 and 4.1.4). Finally, we briefly describe the use of decompositions for matrix inversion, although one rarely needs to invert a matrix (Sect. 4.1.5). Monographs [15,31,37] and [59] include extensive discussions of matrix decompositions.
All mentioned decompositions allow us to transform a general system of
linear equations to a system with an upper triangular, a diagonal, or
a lower triangular coefficient matrix:
![]() , or
, or
![]() , respectively. Such systems are easy to solve with a very
high accuracy by back substitution, see [34]. Assuming the
respective coefficient matrix
, respectively. Such systems are easy to solve with a very
high accuracy by back substitution, see [34]. Assuming the
respective coefficient matrix
![]() has a full rank, one can
find a solution of
has a full rank, one can
find a solution of
![]() , where
, where
![]() , by evaluating
, by evaluating
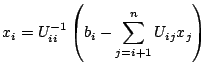 |
(4.1) |
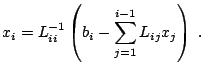 |
(4.2) |
The Cholesky factorization, first published by [5], was
originally developed to solve least squares problems in geodesy and
topography. This factorization, in statistics also referred to as
''square root method,'' is a triangular decomposition. Providing
matrix
![]() is positive definite, the Cholesky decomposition finds
a triangular matrix
is positive definite, the Cholesky decomposition finds
a triangular matrix
![]() that multiplied by its own transpose leads
back to matrix
that multiplied by its own transpose leads
back to matrix
![]() . That is,
. That is,
![]() can be thought of as a square
root of
can be thought of as a square
root of
![]() .
.
The matrix
![]() is called the Cholesky factor of
is called the Cholesky factor of
![]() and the
relation
and the
relation
![]() is called the Cholesky factorization.
is called the Cholesky factorization.
Obviously, decomposing a system
![]() to
to
![]() allows us to solve two triangular systems:
allows us to solve two triangular systems:
![]() for
for
![]() and then
and then
![]() for
for
![]() . This is similar to
the original Gauss approach for solving a positive definite system of
normal equations
. This is similar to
the original Gauss approach for solving a positive definite system of
normal equations
![]() . Gauss solved the
normal equations by a symmetry-preserving elimination and used the
back substitution to solve for
. Gauss solved the
normal equations by a symmetry-preserving elimination and used the
back substitution to solve for
![]() .
.
Let us now describe the algorithm for finding the Cholesky
decomposition, which is illustrated on Fig. 4.1. One of the
interesting features of the algorithm is that in the ![]() th iteration
we obtain the Cholesky decomposition of the
th iteration
we obtain the Cholesky decomposition of the ![]() th leading principal
minor of
th leading principal
minor of
![]() ,
,
![]() .
.
for ![]() to
to ![]()
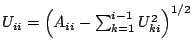
for ![]()
to ![]()
![]()
end
end
The Cholesky decomposition described in Algorithm 1 is
a numerically stable procedure, see [44] and
[45], which can be at the same time implemented in a very
efficient way. Computed values ![]() can be stored in place of
original
can be stored in place of
original ![]() , and thus, no extra memory is needed. Moreover, let
us note that while Algorithm 1 describes the rowwise
decomposition (
, and thus, no extra memory is needed. Moreover, let
us note that while Algorithm 1 describes the rowwise
decomposition (
![]() is computed row by row), there are also
a columnwise version and a version with diagonal pivoting, which is
also applicable to semidefinite matrices. Finally, there are also
modifications of the algorithm, such as blockwise decomposition, that
are suitable for very large problems and parallelization; see
[7,14] and [50].
is computed row by row), there are also
a columnwise version and a version with diagonal pivoting, which is
also applicable to semidefinite matrices. Finally, there are also
modifications of the algorithm, such as blockwise decomposition, that
are suitable for very large problems and parallelization; see
[7,14] and [50].
The LU decomposition is another method reducing a square matrix
![]() to a product of two triangular matrices (lower triangular
to a product of two triangular matrices (lower triangular
![]() and
upper triangular
and
upper triangular
![]() ). Contrary to the Cholesky decomposition, it
does not require a positive definite matrix
). Contrary to the Cholesky decomposition, it
does not require a positive definite matrix
![]() , but there is no
guarantee that
, but there is no
guarantee that
![]() .
.
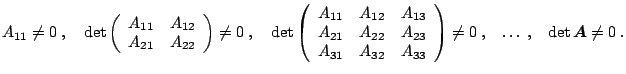 |
Similarly to the Cholesky decomposition, the LU decomposition reduces
solving a system of linear equations
![]() to
solving two triangular systems:
to
solving two triangular systems:
![]() , where
, where
![]() , and
, and
![]() .
.
Finding the LU decomposition of
![]() is described in
Algorithm 2. Since it is equivalent to solving a system of
linear equations by the Gauss elimination, which searches just for
is described in
Algorithm 2. Since it is equivalent to solving a system of
linear equations by the Gauss elimination, which searches just for
![]() and ignores
and ignores
![]() , we refer a reader to Sect. 4.2,
where its advantages (e.g., easy implementation, speed) and
disadvantages (e.g., numerical instability without pivoting) are
discussed.
, we refer a reader to Sect. 4.2,
where its advantages (e.g., easy implementation, speed) and
disadvantages (e.g., numerical instability without pivoting) are
discussed.
Finally, note that there are also generalizations of LU to non-square and singular matrices, such as rank revealing LU factorization; see [51] and [47].
One of the most important matrix transformations is the QR
decomposition. It splits a general matrix
![]() to an orthonormal
matrix
to an orthonormal
matrix
![]() , that is, a matrix with columns orthogonal to each other
and its Euclidian norm equal to
, that is, a matrix with columns orthogonal to each other
and its Euclidian norm equal to ![]() , and to an upper triangular matrix
, and to an upper triangular matrix
![]() . Thus, a suitably chosen orthogonal matrix
. Thus, a suitably chosen orthogonal matrix
![]() will
triangularize the given matrix
will
triangularize the given matrix
![]() .
.
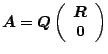 |
If
![]() is a nonsingular square matrix, an even slightly stronger
result can be obtained: uniqueness of the QR decomposition.
is a nonsingular square matrix, an even slightly stronger
result can be obtained: uniqueness of the QR decomposition.
The use of the QR decomposition for solving a system of equations
![]() consists in multiplying the whole system by
the orthonormal matrix
consists in multiplying the whole system by
the orthonormal matrix
![]() ,
,
![]() , and then
solving the remaining upper triangular system
, and then
solving the remaining upper triangular system
![]() . This method guarantees numerical stability by minimizing errors
caused by machine roundoffs (see the end of this section for details).
. This method guarantees numerical stability by minimizing errors
caused by machine roundoffs (see the end of this section for details).
The QR decomposition is usually constructed by finding one orthonormal
vector (one column of
![]() ) after another. This can be achieved using
the so-called elementary orthogonal transformations such as
Householder reflections, [39], or Givens rotations,
[20], that are described in the following subsections. These
transformations are related to the solution of the following standard
task.
) after another. This can be achieved using
the so-called elementary orthogonal transformations such as
Householder reflections, [39], or Givens rotations,
[20], that are described in the following subsections. These
transformations are related to the solution of the following standard
task.
The QR decomposition using Householder reflections (HR) was developed
by [21]. Householder reflection (or Householder
transformation) is a matrix
![]() ,
,
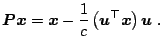 |
To solve Problem 1 using some HR, we search for a vector
![]() such that
such that
![]() will be reflected to the
will be reflected to the ![]() -axis. This holds
for the following choice of
-axis. This holds
for the following choice of
![]() :
:
A Givens rotation (GR) in ![]() dimensions (or Givens transformation) is
defined by an orthonormal matrix
dimensions (or Givens transformation) is
defined by an orthonormal matrix
![]() ,
,
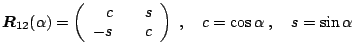 |
Now, let us have a look at how GRs can be used for solving
Problem 1. A GR of a vector
![]() by an angle
by an angle ![]() results in
results in
![]() such that
such that
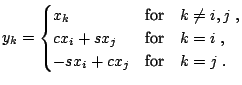 |
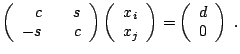 |
The next step employs a simple fact that the pre- or
postmultiplication of a vector
![]() or a matrix
or a matrix
![]() by any GR
by any GR
![]() affects only the
affects only the ![]() th and
th and ![]() th rows and columns,
respectively. Hence, one can combine several rotations without one
rotation spoiling the result of another rotation. (Consequently, GRs
are more flexible than HRs). Two typical ways how GRs are used for
solving Problem 1 mentioned in Sect. 4.1.3 follow.
th rows and columns,
respectively. Hence, one can combine several rotations without one
rotation spoiling the result of another rotation. (Consequently, GRs
are more flexible than HRs). Two typical ways how GRs are used for
solving Problem 1 mentioned in Sect. 4.1.3 follow.
Finally, there are several algorithms for computing the Givens
rotations that improve over the straightforward evaluation of
![]() . A robust algorithm minimizing the loss of precision
is given in [7]. An algorithm minimizing memory
requirements was proposed by [58]. On the other hand,
[16] and [29] proposed modifications aiming to
minimize the number of arithmetic operations.
. A robust algorithm minimizing the loss of precision
is given in [7]. An algorithm minimizing memory
requirements was proposed by [58]. On the other hand,
[16] and [29] proposed modifications aiming to
minimize the number of arithmetic operations.
An appropriate combination of HRs or GRs, respectively, can be used to
compute the QR decomposition of a given matrix
![]() ,
, ![]() , in a following way. Let
, in a following way. Let
![]() ,
,
![]() , denote an orthonormal matrix in
, denote an orthonormal matrix in
![]() such that premultiplication of
such that premultiplication of
![]() by
by
![]() can zero all elements in the
can zero all elements in the ![]() th column that are
below the diagonal and such that the previous columns
th column that are
below the diagonal and such that the previous columns
![]() are not affected at all. Such a matrix can be a blockwise diagonal
matrix with blocks being the identity matrix
are not affected at all. Such a matrix can be a blockwise diagonal
matrix with blocks being the identity matrix
![]() and
a matrix
and
a matrix
![]() solving Problem 1 for the
vector composed of elements in the
solving Problem 1 for the
vector composed of elements in the ![]() th column of
th column of
![]() that
lie on and below the diagonal. The first part
that
lie on and below the diagonal. The first part
![]() guarantees that the columns
guarantees that the columns
![]() of matrix
of matrix
![]() are
not affected by multiplication, whereas the second block
are
not affected by multiplication, whereas the second block
![]() transforms all elements in the
transforms all elements in the ![]() th column that are below the
diagonal to zero. Naturally, matrix
th column that are below the
diagonal to zero. Naturally, matrix
![]() can be found by means
of HRs or GRs as described in previous paragraphs.
can be found by means
of HRs or GRs as described in previous paragraphs.
This way, we construct a series of matrices
![]() such that
such that
![$\displaystyle \boldsymbol{Q}[n] \cdots \boldsymbol{Q}_{1} \boldsymbol{A} = \left(\begin{array}{c}\boldsymbol{R}\\ \boldsymbol{0}\end{array}\right)\;.$](img1541.gif) |
![$\displaystyle \boldsymbol{A} = (\boldsymbol{Q}[n] \cdots \boldsymbol{Q}_{1})^{\...
...mbol{Q} \left(\begin{array}{c}\boldsymbol{R}\\ \boldsymbol{0}\end{array}\right)$](img1544.gif) |
We describe now the QR algorithm using HRs or GRs. Let
![]() denote the orthonormal matrix from Problem 1 constructed
for a vector
denote the orthonormal matrix from Problem 1 constructed
for a vector
![]() by one of the discussed methods.
by one of the discussed methods.
for to
![\begin{displaymath}\boldsymbol{Q}[i] = \left(
\begin{array}{cc}
\boldsymbol{I}_{...
...ol{0} & \boldsymbol{M}(\boldsymbol{x}) \\
\end{array} \right)
\end{displaymath}](img1549.gif)
end
There are also modifications of this basic algorithm employing pivoting for better numerical performance and even revealing rank of the system, see [38] and [36] for instance. An error analysis of the QR decomposition by HRs and GRs are given by [17] and [36], respectively.
Given a nonsingular matrix
![]() , the
Gram-Schmidt orthogonalization constructs a matrix
, the
Gram-Schmidt orthogonalization constructs a matrix
![]() such that
the columns of
such that
the columns of
![]() are orthonormal to each other and span the same
space as the columns of
are orthonormal to each other and span the same
space as the columns of
![]() . Thus,
. Thus,
![]() can be expressed as
can be expressed as
![]() multiplied by another matrix
multiplied by another matrix
![]() , whereby the Gram-Schmidt
orthogonalization process (GS) ensures that
, whereby the Gram-Schmidt
orthogonalization process (GS) ensures that
![]() is an upper
triangular matrix. Consequently, GS can be used to construct the QR
decomposition of a matrix
is an upper
triangular matrix. Consequently, GS can be used to construct the QR
decomposition of a matrix
![]() . A survey of GS variants and their
properties is given by [6].
. A survey of GS variants and their
properties is given by [6].
The classical Gram-Schmidt (CGS) process constructs the orthonormal
basis stepwise. The first column
![]() of
of
![]() is simply
normalized
is simply
normalized
![]() . Having constructed a orthonormal base
. Having constructed a orthonormal base
![]() , the next column
, the next column
![]() is
proportional to
is
proportional to
![]() minus its projection to the space
span
minus its projection to the space
span![]() . Thus,
. Thus,
![]() is by its definition orthogonal to
span
is by its definition orthogonal to
span![]() , and at the same time, the first
, and at the same time, the first ![]() columns of
columns of
![]() and
and
![]() span the same linear space. The elements of the
triangular matrix
span the same linear space. The elements of the
triangular matrix
![]() from Theorem 3 are then coordinates
of the columns of
from Theorem 3 are then coordinates
of the columns of
![]() given the columns of
given the columns of
![]() as a basis.
as a basis.
for to for to
end
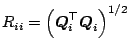
end
Similarly to many decomposition algorithms, also CGS allows a memory
efficient implementation since the computed orthonormal columns of
![]() can rewrite the original columns of
can rewrite the original columns of
![]() . Despite this feature
and mathematical correctness, the CGS algorithm does not always behave
well numerically because numerical errors can very quickly
accumulate. For example, an error made in computing
. Despite this feature
and mathematical correctness, the CGS algorithm does not always behave
well numerically because numerical errors can very quickly
accumulate. For example, an error made in computing
![]() affects
affects
![]() , errors in both of these terms (although caused initially
just by an error in
, errors in both of these terms (although caused initially
just by an error in
![]() ) adversely influence
) adversely influence
![]() and so
on. Fortunately, there is a modified Gram-Schmidt (MGS) procedure,
which prevents such an error accumulation by subtracting linear
combinations of
and so
on. Fortunately, there is a modified Gram-Schmidt (MGS) procedure,
which prevents such an error accumulation by subtracting linear
combinations of
![]() directly from
directly from
![]() before constructing
following orthonormal vectors. (Surprisingly, MGS is historically
older than CGS.)
before constructing
following orthonormal vectors. (Surprisingly, MGS is historically
older than CGS.)
for to
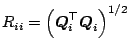
for to
end
end Apart from this algorithm (the row version of MGS), there are also a column version of MGS by [6] and MGS modifications employing iterative orthogonalization and pivoting by [9]. Numerical superiority of MGS over CGS was experimentally established already by [53]. This result is also theoretically supported by the GS error analysis in [6], who uncovered numerical equivalence of the QR decompositions done by MGS and HRs.
The singular value decomposition (SVD) plays an important role in
numerical linear algebra and in many statistical techniques as
well. Using two orthonormal matrices, SVD can diagonalize any matrix
![]() and the results of SVD can tell a lot about (numerical)
properties of the matrix. (This is closely related to the eigenvalue
decomposition: any symmetric square matrix
and the results of SVD can tell a lot about (numerical)
properties of the matrix. (This is closely related to the eigenvalue
decomposition: any symmetric square matrix
![]() can be diagonalized,
can be diagonalized,
![]() , where
, where
![]() is a diagonal matrix
containing the eigenvalues of
is a diagonal matrix
containing the eigenvalues of
![]() and
and
![]() is an orthonormal
matrix.)
is an orthonormal
matrix.)
Similarly to the QR decomposition, SVD offers a numerically stable way
to solve a system of linear equations. Given a system
![]() , one can transform it to
, one can transform it to
![]() and solve it in two trivial
steps: first, finding a solution
and solve it in two trivial
steps: first, finding a solution
![]() of
of
![]() ,
and second, setting
,
and second, setting
![]() , which is equivalent to
, which is equivalent to
![]() .
.
On the other hand, the power of SVD lies in its relation to many
important matrix properties; see [62], for
instance. First of all, the singular values of a matrix
![]() are
equal to the (positive) square roots of the eigenvalues of
are
equal to the (positive) square roots of the eigenvalues of
![]() and
and
![]() , whereby the associated left
and right singular vectors are identical with the corresponding
eigenvectors. Thus, one can compute the eigenvalues of
, whereby the associated left
and right singular vectors are identical with the corresponding
eigenvectors. Thus, one can compute the eigenvalues of
![]() directly from the original matrix
directly from the original matrix
![]() . Second, the number of
nonzero singular values equals the rank of a matrix. Consequently, SVD
can be used to find an effective rank of a matrix, to check a near
singularity and to compute the condition number of a matrix. That is,
it allows to assess conditioning and sensitivity to errors of a given
system of equations. Finally, let us note that there are far more uses
of SVD: identification of the null space of
. Second, the number of
nonzero singular values equals the rank of a matrix. Consequently, SVD
can be used to find an effective rank of a matrix, to check a near
singularity and to compute the condition number of a matrix. That is,
it allows to assess conditioning and sensitivity to errors of a given
system of equations. Finally, let us note that there are far more uses
of SVD: identification of the null space of
![]() ,
,
![]() span
span![]() ; computation of the matrix
pseudo-inverse,
; computation of the matrix
pseudo-inverse,
![]() ; low-rank
approximations and so on. See [7] and [62] for
details.
; low-rank
approximations and so on. See [7] and [62] for
details.
Let us now present an overview of algorithms for computing the SVD
decomposition, which are not described in details due to their extent.
The first stable algorithm for computing the SVD was suggested by
[22]. It involved reduction of a matrix
![]() to its
bidiagonal form by HRs, with singular values and vectors being
computed as eigenvalues and eigenvectors of a specific tridiagonal
matrix using a method based on Sturm sequences. The final form of the
QR algorithm for computing SVD, which has been the preferred SVD
method for dense matrices up to now, is due to [23];
see [2,7] or [15] for the
description of the algorithm and some modifications. An alternative
approach based on Jacobi algorithm was given by
[30]. Latest contributions to the pool of computational
methods for SVD, including [63,10] and
[36], aim to improve the accuracy of singular values and
computational speed using recent advances in the QR decomposition.
to its
bidiagonal form by HRs, with singular values and vectors being
computed as eigenvalues and eigenvectors of a specific tridiagonal
matrix using a method based on Sturm sequences. The final form of the
QR algorithm for computing SVD, which has been the preferred SVD
method for dense matrices up to now, is due to [23];
see [2,7] or [15] for the
description of the algorithm and some modifications. An alternative
approach based on Jacobi algorithm was given by
[30]. Latest contributions to the pool of computational
methods for SVD, including [63,10] and
[36], aim to improve the accuracy of singular values and
computational speed using recent advances in the QR decomposition.
In previous sections, we described how matrix decompositions can be
used for solving systems of linear equations. Let us now discuss the
use of matrix decompositions for inverting a nonsingular squared
matrix
![]() , although matrix
inversion is not needed very often. All discussed matrix decomposition
construct two or more matrices
, although matrix
inversion is not needed very often. All discussed matrix decomposition
construct two or more matrices
![]() such that
such that
![]() , where matrices
, where matrices
![]() are orthonormal, triangular, or
diagonal. Because
are orthonormal, triangular, or
diagonal. Because
![]() we just need to be able to invert
orthonormal and triangular matrices (a diagonal matrix is a special
case of a triangular matrix).
we just need to be able to invert
orthonormal and triangular matrices (a diagonal matrix is a special
case of a triangular matrix).
First, an orthonormal matrix
![]() satisfies by definition
satisfies by definition
![]() . Thus, inversion is in this case
equivalent to the transposition of a matrix:
. Thus, inversion is in this case
equivalent to the transposition of a matrix:
![]() .
.
Second, inverting an upper triangular matrix
![]() can be done by
solving directly
can be done by
solving directly
![]() , which leads to the backward
substitution method. Let
, which leads to the backward
substitution method. Let
![]() denote
the searched for inverse matrix
denote
the searched for inverse matrix
![]() .
.
for to
for to
end
end There are several other algorithms available such as forward substitution or blockwise inversion. Designed for a faster and more (time) efficient computation, their numerical behavior does not significantly differ from the presented algorithm. See [8] for an overview and numerical study.