Stochastic approximation (SA) is a cornerstone of stochastic
optimization. Robbins and Monro (1951) introduced SA as a general
root-finding method when only noisy measurements of the underlying
function are available. Let us now discuss some aspects of SA as
applied to the more specific problem of root-finding in the context of
optimization. With a differentiable loss function
![]() , recall the familiar set of
, recall the familiar set of ![]() equations and
equations and ![]() unknowns for use in finding a minimum
unknowns for use in finding a minimum
![]() :
:
To motivate the general SA approach, first recall the familiar form for the unconstrained deterministic steepest descent algorithm for solving (6.3):
Unlike with steepest descent, it is assumed here that we have no
direct knowledge of
![]() . The recursive procedure of interest
is in the general SA form
. The recursive procedure of interest
is in the general SA form
Sections 6.3.2 and 6.3.3 discuss two SA methods for carrying out the optimization task using noisy measurements of the loss function. Section 6.3.2 discusses the traditional finite-difference SA method and Sect. 6.3.3 discusses the more recent simultaneous perturbation method.
The essential part of (6.4) is the gradient approximation
![]() . The traditional means of forming the
approximation is the finite-difference
method. Expression (6.4) with this approximation represents
the finite-difference SA (FDSA) algorithm. One-sided gradient
approximations involve measurements
. The traditional means of forming the
approximation is the finite-difference
method. Expression (6.4) with this approximation represents
the finite-difference SA (FDSA) algorithm. One-sided gradient
approximations involve measurements
![]() and
and
![]() perturbation
perturbation![]() , while two-sided
approximations involve measurements of the form
, while two-sided
approximations involve measurements of the form
![]() perturbation
perturbation![]() . The two-sided FD approximation for use
with (6.4) is
. The two-sided FD approximation for use
with (6.4) is
It is of fundamental importance to determine conditions such that
![]() as shown in (6.4) and (6.5)
converges to
as shown in (6.4) and (6.5)
converges to
![]() in some appropriate stochastic sense. The
convergence theory for the FDSA algorithm is similar to ''standard''
convergence theory for the root-finding SA algorithm of Robbins and
Monro (1951). Additional difficulties, however, arise due to a bias in
in some appropriate stochastic sense. The
convergence theory for the FDSA algorithm is similar to ''standard''
convergence theory for the root-finding SA algorithm of Robbins and
Monro (1951). Additional difficulties, however, arise due to a bias in
![]() as an estimator of
as an estimator of
![]() . That is, standard conditions for convergence of
SA require unbiased estimates of
. That is, standard conditions for convergence of
SA require unbiased estimates of
![]() at all
at all ![]() . On
the other hand,
. On
the other hand,
![]() , as shown
in (6.5), is a biased estimator, with the bias having
a magnitude of order
, as shown
in (6.5), is a biased estimator, with the bias having
a magnitude of order ![]() . We will not present the details of
the convergence theory here, as it is available in many other
references (e.g., Fabian, 1971; Kushner and Yin, 1997, Sects. 5.3,
8.3, and 10.3; Ruppert, 1991; Spall, 2003, Chap. 6). However, let us
note that the standard conditions on the gain sequences are:
. We will not present the details of
the convergence theory here, as it is available in many other
references (e.g., Fabian, 1971; Kushner and Yin, 1997, Sects. 5.3,
8.3, and 10.3; Ruppert, 1991; Spall, 2003, Chap. 6). However, let us
note that the standard conditions on the gain sequences are: ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() . The
choice of these gain sequences is critical to the performance of the
method. Common forms for the sequences are:
. The
choice of these gain sequences is critical to the performance of the
method. Common forms for the sequences are:
Let us summarize a numerical example based on the following ![]() loss function:
loss function:
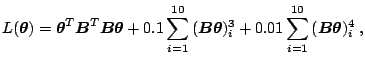 |
Using ![]() loss measurements per run, we compare FDSA with the
localized random search method of Sect. 6.2. Based on
principles for gain selection in Spall (2003, Sect. 6.6) together with
some limited trial-and-error experimentation, we chose
loss measurements per run, we compare FDSA with the
localized random search method of Sect. 6.2. Based on
principles for gain selection in Spall (2003, Sect. 6.6) together with
some limited trial-and-error experimentation, we chose ![]() ,
, ![]() ,
, ![]() ,
,
![]() , and
, and
![]() for FDSA and an average of
for FDSA and an average of ![]() loss measurements per
iteration with normally distributed perturbations having distribution
loss measurements per
iteration with normally distributed perturbations having distribution
![]() for the random search
method.
for the random search
method.
Figure 6.2 summarizes the results. Each curve represents the
sample mean of ![]() independent replications. An individual
replication of one of the two algorithms has much more variation than
the corresponding smoothed curve in the figure.
independent replications. An individual
replication of one of the two algorithms has much more variation than
the corresponding smoothed curve in the figure.
![\includegraphics[width=8.5cm]{text/2-6/fig2.eps}](img2255.gif)
|
Figure 6.2 shows that both algorithms produce an overall
reduction in the (true) loss function as the number of measurements
approach ![]() . The curves illustrate that FDSA outperforms random
search in this case. To make the comparison fair, attempts were made
to tune each algorithm to provide approximately the best performance
possible. Of course, one must be careful about using this example to
infer that such a result will hold in other problems as well.
. The curves illustrate that FDSA outperforms random
search in this case. To make the comparison fair, attempts were made
to tune each algorithm to provide approximately the best performance
possible. Of course, one must be careful about using this example to
infer that such a result will hold in other problems as well.
The FDSA algorithm of Sect. 6.3.2 is a standard SA method for
carrying out optimization with noisy measurement of the loss
function. However, as the dimension ![]() grows large, the number of
loss measurements required may become prohibitive. That is, each
two-sided gradient approximation requires
grows large, the number of
loss measurements required may become prohibitive. That is, each
two-sided gradient approximation requires ![]() loss measurements. More
recently, the simultaneous perturbation SA (SPSA) method was
introduced, requiring only two measurements per iteration to form
a gradient approximation independent of the dimension
loss measurements. More
recently, the simultaneous perturbation SA (SPSA) method was
introduced, requiring only two measurements per iteration to form
a gradient approximation independent of the dimension ![]() . This
provides the potential for a large savings in the overall cost of
optimization.
. This
provides the potential for a large savings in the overall cost of
optimization.
Beginning with the generic SA form in (6.4), we now present
the SP form of the gradient approximation. In this form, all elements
of
![]() are randomly perturbed together to obtain two
loss measurements
are randomly perturbed together to obtain two
loss measurements ![]() . For the two-sided SP gradient
approximation, this leads to
. For the two-sided SP gradient
approximation, this leads to
Relative to FDSA, the ![]() -fold measurement savings per iteration, of
course, provides only the potential for SPSA to achieve large
savings in the total number of measurements required to estimate
-fold measurement savings per iteration, of
course, provides only the potential for SPSA to achieve large
savings in the total number of measurements required to estimate
![]() when
when ![]() is large. This potential is realized if the
number of iterations required for effective convergence to an optimum
is large. This potential is realized if the
number of iterations required for effective convergence to an optimum
![]() does not increase in a way to cancel the measurement
savings per gradient approximation. One can use asymptotic
distribution theory to address this issue. In particular, both FDSA
and SPSA are known to be asymptotically normally distributed under
very similar conditions. One can use this asymptotic distribution
result to characterize the mean-squared error
does not increase in a way to cancel the measurement
savings per gradient approximation. One can use asymptotic
distribution theory to address this issue. In particular, both FDSA
and SPSA are known to be asymptotically normally distributed under
very similar conditions. One can use this asymptotic distribution
result to characterize the mean-squared error
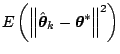 for the two
algorithms for large
for the two
algorithms for large ![]() . Fortunately, under fairly broad conditions,
the
. Fortunately, under fairly broad conditions,
the ![]() -fold savings at each iteration is preserved
across iterations. In particular, based on asymptotic
considerations:
-fold savings at each iteration is preserved
across iterations. In particular, based on asymptotic
considerations:
![% latex2html id marker 24579
\framebox[\textwidth]{
\parbox{\textwidth}{Under r...
...radient approximation uses only $1 / p$\ the number of
function evaluations).}}](img2264.gif)
The SPSA Web site (www.jhuapl.edu/SPSA) includes many references on the theory and application of SPSA. On this Web site, one can find many accounts of numerical studies that are consistent with the efficiency statement above. (Of course, given that the statement is based on asymptotic arguments and associated regularity conditions, one should not assume that the result always holds.) In addition, there are references describing many applications. These include queuing systems, pattern recognition, industrial quality improvement, aircraft design, simulation-based optimization, bioprocess control, neural network training, chemical process control, fault detection, human-machine interaction, sensor placement and configuration, and vehicle traffic management.
We will not present the formal conditions for convergence and
asymptotic normality of SPSA, as such conditions are available in many
references (e.g., Dippon and Renz, 1997; Gerencsér, 1999; Spall, 1992,
2003, Chap. 7). These conditions are essentially identical to the
standard conditions for convergence of SA algorithms, with the
exception of the additional conditions on the user-generated
perturbation vector
![]() .
.
The choice of the distribution for generating the
![]() is important to the performance of the
algorithm. The standard conditions for the elements
is important to the performance of the
algorithm. The standard conditions for the elements
![]() of
of
![]() are that the
are that the
![]() are independent
for all
are independent
for all ![]() ,
, ![]() , identically distributed for all
, identically distributed for all ![]() at each
at each ![]() ,
symmetrically distributed about zero and uniformly bounded in
magnitude for all
,
symmetrically distributed about zero and uniformly bounded in
magnitude for all ![]() . In addition, there is an important inverse
moments condition:
. In addition, there is an important inverse
moments condition:
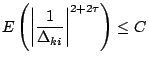 |
As with any real-world implementation of stochastic optimization,
there are important practical considerations when using SPSA. One is
to attempt to define
![]() so that the magnitudes of the
so that the magnitudes of the
![]() elements are similar to one another. This desire is
apparent by noting that the magnitudes of all components in the
perturbations
elements are similar to one another. This desire is
apparent by noting that the magnitudes of all components in the
perturbations
![]() are identical in the case where
identical Bernoulli distributions are used. Although it is not always
possible to choose the definition of the elements in
are identical in the case where
identical Bernoulli distributions are used. Although it is not always
possible to choose the definition of the elements in
![]() , in most cases an analyst will have the flexibility
to specify the units for
, in most cases an analyst will have the flexibility
to specify the units for
![]() to ensure similar
magnitudes. Another important consideration is the choice of the
gains
to ensure similar
magnitudes. Another important consideration is the choice of the
gains ![]() ,
, ![]() . The principles described for FDSA above apply
to SPSA as well. Section 7.5 of Spall (2003) provides additional
practical guidance.
. The principles described for FDSA above apply
to SPSA as well. Section 7.5 of Spall (2003) provides additional
practical guidance.
There have been a number of important extensions of the basic SPSA method represented by the combination of (6.4) and (6.6). Three such extensions are to the problem of global (versus local) optimization, to discrete (versus continuous) problems, and to include second-order-type information (Hessian matrix) with the aim of creating a stochastic analogue to the deterministic Newton-Raphson method.
The use of SPSA for global minimization among multiple local minima is discussed in Maryak and Chin (2001). One of their approaches relies on injecting Monte Carlo noise in the right-hand side of the basic SPSA updating step in (6.4). This approach is a common way of converting SA algorithms to global optimizers through the additional ''bounce'' introduced into the algorithm (Yin, 1999). Maryak and Chin (2001) also show that basic SPSA without injected noise (i.e., (6.4) and (6.6) without modification) may, under certain conditions, be a global optimizer. Formal justification for this result follows because the random error in the SP gradient approximation acts in a way that is statistically equivalent to the injected noise mentioned above.
Discrete optimization problems (where
![]() may take on
discrete or combined discrete/continuous values) are discussed in
Gerencsér et al. (1999). Discrete SPSA relies on a fixed-gain
(constant
may take on
discrete or combined discrete/continuous values) are discussed in
Gerencsér et al. (1999). Discrete SPSA relies on a fixed-gain
(constant ![]() and
and ![]() ) version of the standard SPSA
method. The parameter estimates produced are constrained to lie on
a discrete-valued grid. Although gradients do not exist in this
setting, the approximation in (6.6) (appropriately modified)
is still useful as an efficient measure of slope information.
) version of the standard SPSA
method. The parameter estimates produced are constrained to lie on
a discrete-valued grid. Although gradients do not exist in this
setting, the approximation in (6.6) (appropriately modified)
is still useful as an efficient measure of slope information.
Finally, using the simultaneous perturbation idea, it is possible to
construct a simple method for estimating the Hessian (or Jacobian)
matrix of ![]() while, concurrently, estimating the primary parameters
of interest (
while, concurrently, estimating the primary parameters
of interest (
![]() ). This adaptive SPSA (ASP) approach
produces a stochastic analogue to the deterministic Newton-Raphson
algorithm (e.g., Bazaraa et al., 1993, pp. 308-312), leading to
a recursion that is optimal or near-optimal in its rate of convergence
and asymptotic error. The approach applies in both the gradient-free
setting emphasized in this section and in the root-finding/stochastic
gradient-based (Robbins-Monro) setting reviewed in Spall (2003,
Chaps. 4 and 5). Like the standard SPSA algorithm, the ASP algorithm
requires only a small number of loss function (or gradient, if
relevant) measurements per iteration - independent of the problem
dimension - to adaptively estimate the Hessian and parameters of
primary interest. Further information is available at Spall (2000) or
Spall (2003, Sect. 7.8).
). This adaptive SPSA (ASP) approach
produces a stochastic analogue to the deterministic Newton-Raphson
algorithm (e.g., Bazaraa et al., 1993, pp. 308-312), leading to
a recursion that is optimal or near-optimal in its rate of convergence
and asymptotic error. The approach applies in both the gradient-free
setting emphasized in this section and in the root-finding/stochastic
gradient-based (Robbins-Monro) setting reviewed in Spall (2003,
Chaps. 4 and 5). Like the standard SPSA algorithm, the ASP algorithm
requires only a small number of loss function (or gradient, if
relevant) measurements per iteration - independent of the problem
dimension - to adaptively estimate the Hessian and parameters of
primary interest. Further information is available at Spall (2000) or
Spall (2003, Sect. 7.8).