6.4 Genetic Algorithms

Genetic algorithms (GAs) represent a popular approach to stochastic optimization, especially as relates to the global optimization problem of finding the best solution among multiple local mimima. (GAs may be used in general search problems that are not directly represented as stochastic optimization problems, but we focus here on their use in optimization.) GAs represent a special case of the more general class of evolutionary computation algorithms (which also includes methods such as evolutionary programming and evolution strategies). The GA applies when the elements of $\boldsymbol {\theta }$ are real-, discrete-, or complex-valued. As suggested by the name, the GA is based loosely on principles of natural evolution and survival of the fittest. In fact, in GA terminology, an equivalent maximization criterion, such as $-L(\boldsymbol{\theta})$ (or its analogue based on a bit-string form of $\boldsymbol {\theta }$ ), is often referred to as the fitness function to emphasize the evolutionary concept of the fittest of a species.

A fundamental difference between GAs and the random search and SA algorithms considered in Sects. 6.2 and 6.3 is that GAs work with a population of candidate solutions to the problem. The previous algorithms worked with one solution and moved toward the optimum by updating this one estimate. GAs simultaneously consider multiple candidate solutions to the problem of minimizing

and iterate by moving this population of solutions toward a global optimum. The terms generation and iteration are used interchangeably to describe the process of transforming one population of solutions to another. Figure 6.3 illustrates the successful operations of a GA for a population of size

with problem dimension

. In this conceptual illustration, the population of solutions eventually come together at the global optimum.

**Figure 6.3:** Minimization of multimodal loss function. Successful operations of a GA with a population of candidate solutions clustering around the global minimum after some number of iterations (generations) (Reprinted from *Introduction to Stochastic Search and Optimization* with permission of John Wiley & Sons, Inc.)
$\includegraphics[width=10cm,bb=164 492 447 575,clip]{text/2-6/fig3.eps}$

The use of a population versus a single solution affects in a basic way the range of practical problems that can be considered. In particular, GAs tend to be best suited to problems where the loss function evaluations are computer-based calculations such as complex function evaluations or simulations. This contrasts with the single-solution approaches discussed earlier, where the loss function evaluations may represent computer-based calculations or physical experiments. Population-based approaches are not generally feasible when working with real-time physical experiments. Implementing a GA with physical experiments requires that either there be multiple identical experimental setups (parallel processing) or that the single experimental apparatus be set to the same state prior to each population member's loss evaluation (serial processing). These situations do not occur often in practice.

Specific values of $\boldsymbol {\theta }$ in the population are referred to as chromosomes. The central idea in a GA is to move a set (population) of chromosomes from an initial collection of values to a point where the fitness function is optimized. We let

denote the population size (number of chromosomes in the population). Most of the early work in the field came from those in the fields of computer science and artificial intelligence. More recently, interest has extended to essentially all branches of business, engineering, and science where search and optimization are of interest. The widespread interest in GAs appears to be due to the success in solving many difficult optimization problems. Unfortunately, to an extent greater than with other methods, some interest appears also to be due to a regrettable amount of ''salesmanship'' and exaggerated claims. (For example, in a recent software advertisement, the claim is made that the software ''... uses GAs to solve any optimization problem.'' Such statements are provably false.) While GAs are important tools within stochastic optimization, there is no formal evidence of consistently superior performance - relative to other appropriate types of stochastic algorithms - in any broad, identifiable class of problems.

Let us now give a very brief historical account. The reader is directed to Goldberg (1989, Chap. 4), Mitchell (1996, Chap. 1), Michalewicz (1996, pp. 1-10), Fogel (2000, Chap. 3), and Spall (2003, Sect. 9.2) for more complete historical discussions. There had been some success in creating mathematical analogues of biological evolution for purposes of search and optimization since at least the 1950s (e.g., Box, 1957). The cornerstones of modern evolutionary computation - evolution strategies, evolutionary programming, and GAs - were developed independently of each other in the 1960s and 1970s. John Holland at the University of Michigan published the seminal monograph Adaptation in Natural and Artificial Systems (Holland, 1975). There was subsequently a sprinkle of publications, leading to the first full-fledged textbook Goldberg (1989). Activity in GAs grew rapidly beginning in the mid-1980s, roughly coinciding with resurgent activity in other artificial intelligence-type areas such as neural networks and fuzzy logic. There are now many conferences and books in the area of evolutionary computation (especially GAs), together with countless other publications.

6.4.2 Chromosome Coding and the Basic GA Operations

This section summarizes some aspects of the encoding process for the population chromosomes and discusses the selection, elitism, crossover, and mutation operations. These operations are combined to produce the steps of the GA.

An essential aspect of GAs is the encoding of the

values of $\boldsymbol {\theta }$ appearing in the population. This encoding is critical to the GA operations and the associated decoding to return to the natural problem space in $\boldsymbol {\theta }$ . Standard binary

bit strings have traditionally been the most common encoding method, but other methods include gray coding (which also uses

strings, but differs in the way the bits are arranged) and basic computer-based floating-point representation of the real numbers in $\boldsymbol {\theta }$ . This

-character coding is often referred to as real-number coding since it operates as if working with $\boldsymbol {\theta }$ directly. Based largely on successful numerical implementations, this natural representation of $\boldsymbol {\theta }$ has grown more popular over time. Details and further references on the above and other coding schemes are given in Michalewicz (1996, Chap. 5), Mitchell (1996, Sects. 5.2 and 5.3), Fogel (2000, Sects. 3.5 and 4.3), and Spall (2003, Sect. 9.3).

Let us now describe the basic operations mentioned above. For consistency with standard GA terminology, let us assume that $L(\boldsymbol{\theta})$ has been transformed to a fitness function with higher values being better. A common transformation is to simply set the fitness function to $-L(\boldsymbol{\theta}) + C$ , where $C \ge 0$ is a constant that ensures that the fitness function is nonnegative on $\Theta$ (nonnegativity is only required in some GA implementations). Hence, the operations below are described for a maximization problem. It is also assumed here that the fitness evaluations are noise-free. Unless otherwise noted, the operations below apply with any coding scheme for the chromosomes.

Selection and elitism steps occur after evaluating the fitness function for the current population of chromosomes. A subset of chromosomes is selected to use as parents for the succeeding generation. This operation is where the survival of the fittest principle arises, as the parents are chosen according to their fitness value. While the aim is to emphasize the fitter chromosomes in the selection process, it is important that not too much priority is given to the chromosomes with the highest fitness values early in the optimization process. Too much emphasis of the fitter chromosomes may tend to reduce the diversity needed for an adequate search of the domain of interest, possibly causing premature convergence in a local optimum. Hence methods for selection allow with some nonzero probability the selection of chromosomes that are suboptimal.

Associated with the selection step is the optional ''elitism'' strategy, where the $N_{e} < N$ best chromosomes (as determined from their fitness evaluations) are placed directly into the next generation. This guarantees the preservation of the $N_{e}$ best chromosomes at each generation. Note that the elitist chromosomes in the original population are also eligible for selection and subsequent recombination.

As with the coding operation for $\boldsymbol {\theta }$ , many schemes have been proposed for the selection process of choosing parents for subsequent recombination. One of the most popular methods is roulette wheel selection (also called fitness proportionate selection). In this selection method, the fitness functions must be nonnegative on $\Theta$ . An individual's slice of a Monte Carlo-based roulette wheel is an area proportional to its fitness. The ''wheel'' is spun in a simulated fashion $N - N_{e}$ times and the parents are chosen based on where the pointer stops. Another popular approach is called tournament selection. In this method, chromosomes are compared in a ''tournament,'' with the better chromosome being more likely to win. The tournament process is continued by sampling (with replacement) from the original population until a full complement of parents has been chosen. The most common tournament method is the binary approach, where one selects two pairs of chromosomes and chooses as the two parents the chromosome in each pair having the higher fitness value. Empirical evidence suggests that the tournament selection method often performs better than roulette selection. (Unlike tournament selection, roulette selection is very sensitive to the scaling of the fitness function.) Mitchell (1996, Sect. 5.4) provides a good survey of several other selection methods.

The crossover operation creates offspring of the pairs of parents from the selection step. A crossover probability $P_{c}$ is used to determine if the offspring will represent a blend of the chromosomes of the parents. If no crossover takes place, then the two offspring are clones of the two parents. If crossover does take place, then the two offspring are produced according to an interchange of parts of the chromosome structure of the two parents. Figure 6.4 illustrates this for the case of a ten-bit binary representation of the chromosomes. This example shows one-point crossover, where the bits appearing after one randomly chosen dividing (splice) point in the chromosome are interchanged. In general, one can have a number of splice points up to the number of bits in the chromosomes minus one, but one-point crossover appears to be the most commonly used.

Note that the crossover operator also applies directly with real-number coding since there is nothing directly connected to binary coding in crossover. All that is required are two lists of compatible symbols. For example, one-point crossover applied to the chromosomes ( $\boldsymbol {\theta }$ values) $[{6.7}, -{7.4}, {4.0}, {3.9} \vert {6.2}, -{1.5}]$ and $[-{3.8}, {5.3}, {9.2}, -{0.6} \vert {8.4}, -{5.1}$ ] yields the two children:

and

**Figure 6.4:** Example of crossover operator under binary coding with one splice point
$\includegraphics[width=6.4cm]{text/2-6/fig4.eps}$

The final operation we discuss is mutation. Because the initial population may not contain enough variability to find the solution via crossover operations alone, the GA also uses a mutation operator where the chromosomes are randomly changed. For the binary coding, the mutation is usually done on a bit-by-bit basis where a chosen bit is flipped from 0 to

, or vice versa. Mutation of a given bit occurs with small probability $P_{m}$ . Real-number coding requires a different type of mutation operator. That is, with a (

)-based coding, an opposite is uniquely defined, but with a real number, there is no clearly defined opposite (e.g., it does not make sense to ''flip'' the

element). Probably the most common type of mutation operator is simply to add small independent normal (or other) random vectors to each of the chromosomes (the $\boldsymbol {\theta }$ values) in the population.

As discussed in Sect. 6.1.4, there is no easy way to know when a stochastic optimization algorithm has effectively converged to an optimum. this includes gas. The one obvious means of stopping a GA is to end the search when a budget of fitness (equivalently, loss) function evaluations has been spent. Alternatively, termination may be performed heuristically based on subjective and objective impressions about convergence. In the case where noise-free fitness measurements are available, criteria based on fitness evaluations may be most useful. for example, a fairly natural criterion suggested in Schwefel (1995, p. 145) is to stop when the maximum and minimum fitness values over the

population values within a generation are sufficiently close to one another. however, this criterion provides no formal guarantee that the algorithm has found a global solution.

6.4.3 The Core Genetic Algorithm

The steps of a basic form of the GA are given below. These steps are general enough to govern many (perhaps most) modern implementations of GAs, including those in modern commercial software. Of course, the performance of a GA typically depends greatly on the implementation details, just as with other stochastic optimization algorithms. Some of these practical implementation issues are taken up in the next section.

Core GA Steps for Noise-Free Fitness Evaluations

6.4.4 Some Implementation Aspects

While the above steps provide the broad outline for many modern implementations of GAs, there are some important implementation aspects that must be decided before a practical implementation. This section outlines a few of those aspects. More detailed discussions are given in Mitchell (1996, Chap. 5), Michalewicz (1996, Chaps. 4-6), Fogel (2000, Chaps. 3 and 4), Goldberg (2002, Chap. 12), and other references mentioned below. A countless number of numerical studies have been reported in the literature; we do not add to that list here.

As with other stochastic optimization methods, the choice of algorithm-specific coefficients has a significant impact on performance. With GAs, there is a relatively large number of user decisions required. The following must be set: the choice of chromosome encoding, the population size (

), the probability distribution generating the initial population, the strategy for parent selection (roulette wheel or otherwise), the number of splice points in the crossover, the crossover probability ( $P_{c}$ ), the mutation probability ( $P_{m}$ ), the number of retained chromosomes in elitism ( $N_{e}$ ), and some termination criterion. Some typical values for these quantities are discussed, for example, in Mitchell (1996, pp. 175-177) and Spall (2003, Sect. 9.6).

Constraints on $L(\boldsymbol{\theta})$ (or the equivalent fitness function) and/or $\boldsymbol {\theta }$ are of major importance in practice. The bit-based implementation of GAs provide a natural way of implementing component-wise lower and upper bounds on the elements of $\boldsymbol {\theta }$ (i.e., a hypercube constraint). More general approaches to handling constraints are discussed in Michalewicz (1996, Chap. 7 and Sects. 4.5 and 15.3) and Michalewicz and Fogel (2000, Chap. 9).

Until now, it has been assumed that the fitness function is observed without noise. One of the two possible defining characteristics of stochastic optimization, however, is optimization with noise in the function measurements (Property I in Sect. 6.1.3). There appears to be relatively little formal analysis of GAs in the presence of noise, although the application and testing of GAs in such cases has been carried out since at least the mid-1970s (e.g., De Jong, 1975, p. 203). A large number of numerical studies are in the literature (e.g., the references and studies in Spall, 2003, Sects. 9.6 and 9.7). As with other algorithms, there is a fundamental tradeoff of more accurate information for each function input (typically, via an averaging of the inputs) and fewer function inputs versus less accurate (''raw'') information to the algorithm together with a greater number of inputs to the algorithm. There appears to be no rigorous comparison of GAs with other algorithms regarding relative robustness to noise. Regarding noise, Michalewicz and Fogel (2000, p. 325) state: ''There really are no effective heuristics to guide the choices to be made that will work in general.''

6.4.5 Some Comments on the Theory for GAs

One of the key innovations in Holland (1975) was the attempt to put GAs on a stronger theoretical footing than the previous ad hoc treatments. He did this by the introduction of schema theory. While many aspects and implications of schema theory have subsequently been challenged (Reeves and Rowe, 2003, Chap. 3; Spall, 2003, Sect. 10.3), some aspects remain viable. In particular, schema theory itself is generally correct (subject to a few modifications), although many of the assumed implications have not been correct. With the appropriate caveats and restrictions, schema theory provides some intuitive explanation for the good performance that is frequently observed with GAs.

More recently, Markov chains have been used to provide a formal structure for analyzing GAs. First, let us mention one negative result. Markov chains can be used to show that a canonical GA without elitism is (in general) provably nonconvergent (Rudolph, 1994). That is, with a GA that does not hold onto the best solution at each generation, there is the possibility (through crossover and mutation) that a chromosome corresponding to $\boldsymbol{\theta}^{\ast}$ will be lost. (Note that the GA without elitism corresponds to the form in Holland, 1975.)

On the other hand, conditions for the formal convergence of GAs to an optimal $\boldsymbol{\theta}^{\ast}$ (or its coded equivalent) are presented in Vose (1999, Chaps. 13 and 14), Fogel (2000, Chap. 4), Reeves and Rowe (2003, Chap. 6), and Spall (2003, Sect. 10.5), among other references. Consider a binary bit-coded GA with a population size of

and a string length of

bits per chromosome. Then the total number of possible unique populations is:

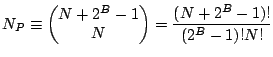$\displaystyle N_{P} \equiv \left(\begin{matrix}{N+2^{B}-1} \\ N \\ \end{matrix}\right) = \frac{(N+2^{B}-1)!}{(2^{B}-1)!N!}$

$\displaystyle \boldsymbol{p}_{k+1}^{T} =\boldsymbol{p}_{k}^{T} \boldsymbol{P}=\boldsymbol{p}_{0}^{T} \boldsymbol{P}^{\,k+1}\;,$

Suppose that $\boldsymbol{\theta}^{\ast}$ is unique (i.e., $\Theta^{\ast}$ is the singleton $\boldsymbol{\theta}^{\ast}$ ). Let $J \subseteq \{1, 2,\ldots, N_{P}\}$ be the set of indices corresponding to the populations that contain at least one chromosome representing $\boldsymbol{\theta}^{\ast}$ . So, for example, if $J = \{1, 6, N_{P} - 3\}$ , then each of the three populations indexed by

and $N_{P} - 3$ contains at least one chromosome that, when decoded, is equal to $\boldsymbol{\theta}^{\ast}$ . Under the above-mentioned assumptions of irreducibility and ergodicity, $\sum\nolimits_{i\in J} {\bar {p}_{i} } = 1$ , where $\bar{p}_{i}$ is the

th element of $\bar {\boldsymbol{p}}$ . Hence, a GA with $N_{e} = 1$ and a transition matrix that is irreducible and ergodic converges in probability to $\boldsymbol{\theta}^{\ast}$ .

To establish the fact of convergence alone, it may not be necessary to compute the $\boldsymbol{P}$ matrix. Rather, it suffices to know that the chain is irreducible and ergodic. (For example, Rudolph, 1997, p. 125, shows that the Markov chain approach yields convergence when $0 < P_{m} < 1$ .) However, $\boldsymbol{P}$ must be explicitly computed to get the rate of convergence information that is available from $\boldsymbol{p}_{k}$ . This is rarely possible in practice because the number of states in the Markov chain (and hence dimension of the Markov transition matrix) grows very rapidly with increases in the population size and/or the number of bits used in coding for the population elements. For example, in even a trivial problem of

, there are $\sim 10^{8}$ states and $\sim 10^{16}$ elements in the transition matrix; this problem is much smaller than any practical GA, which can easily have

population elements and

bits per population element (leading to well over $10^{100}$ states, with each element in the corresponding row and column in the transition matrix requiring significant computation).