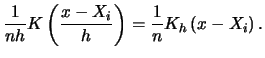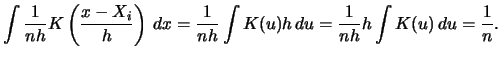Contrary to the treatment of the histogram in statistics textbooks we have shown that the histogram is more than just a convenient tool for giving a graphical representation of an empirical frequency distribution. It is a serious and widely used method for estimating an unknown pdf. Yet, the histogram has some shortcomings and hopefully this chapter will persuade you that the method of kernel density estimation is in many respects preferable to the histogram.
Recall that the shape of the histogram is governed by two
parameters: the binwidth ![]() , and the origin of the bin grid,
, and the origin of the bin grid, ![]() . We
have seen that the averaged shifted histogram is a slick way to free the histogram
from the dependence on the choice of an origin. You may recall that
we have not had similar success in providing a convincing and
applicable rule for choosing the binwidth
. We
have seen that the averaged shifted histogram is a slick way to free the histogram
from the dependence on the choice of an origin. You may recall that
we have not had similar success in providing a convincing and
applicable rule for choosing the binwidth ![]() . There is no
choice-of-an-origin problem in kernel density estimation but you will
soon discover that we will run into the binwidth-selection problem again.
Hopefully, the second time around we will be able to give a better answer
to this challenge.
. There is no
choice-of-an-origin problem in kernel density estimation but you will
soon discover that we will run into the binwidth-selection problem again.
Hopefully, the second time around we will be able to give a better answer
to this challenge.
Even if the ASH seemed to solve the choice-of-an-origin problem the histogram retains some undesirable properties:
Recall that our derivation of the histogram was based on the intuitively plausible idea that
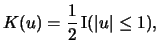 |
(3.3) |
Then we can write (3.2) as
Note from (3.5) that for each observation that falls into the
interval ![]() the indicator function takes on the value
the indicator function takes on the value
![]() , and we get a contribution to our frequency count. But each
contribution is weighted equally (namely by a factor of one), no
matter how close the observation
, and we get a contribution to our frequency count. But each
contribution is weighted equally (namely by a factor of one), no
matter how close the observation ![]() is to
is to ![]() (provided that it is within
(provided that it is within
![]() of
of ![]() ). Maybe we should give more weight to
contributions from observations very
close to
). Maybe we should give more weight to
contributions from observations very
close to ![]() than to those coming from observations that are
more distant.
than to those coming from observations that are
more distant.
For instance, consider the formula
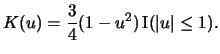
| Kernel | |
| Uniform |
|
| Triangle |
|
| Epanechnikov |
|
| Quartic (Biweight) |
|
| Triweight |
|
| Gaussian |
|
| Cosine |
|
If you look at (3.6) it will be clear that one could
think of the procedure as a slick way of counting the number of
observations that fall into the interval around ![]() , where
contributions from
, where
contributions from ![]() that are close to
that are close to ![]() are weighted
more than those that are further away. The latter property is shared by
the Epanechnikov kernel with many other kernels, some of which we
introduce in Table 3.1.
Figure 3.1 displays some of the kernel functions.
are weighted
more than those that are further away. The latter property is shared by
the Epanechnikov kernel with many other kernels, some of which we
introduce in Table 3.1.
Figure 3.1 displays some of the kernel functions.
![\includegraphics[width=1.4\defpicwidth]{SPMkernel.ps}](spmhtmlimg605.gif)
|
Now we can give the
following general form of the kernel density estimator of a probability
density ![]() , based on a random sample
, based on a random sample
![]() from
from
![]() :
:
Similar to the histogram, ![]() controls the smoothness
of the estimate and the choice of
controls the smoothness
of the estimate and the choice of ![]() is a crucial problem.
Figure 3.2 shows density estimates for the
stock returns data using the Quartic kernel and
different bandwidths.
is a crucial problem.
Figure 3.2 shows density estimates for the
stock returns data using the Quartic kernel and
different bandwidths.
![\includegraphics[width=1.4\defpicwidth]{SPMdensity.ps}](spmhtmlimg612.gif)
|
Again, it is hard to determine which value of ![]() provides the
optimal degree of smoothness
without some formal criterion at hand. This problem will be handled further
below, especially in the Section 3.3.
provides the
optimal degree of smoothness
without some formal criterion at hand. This problem will be handled further
below, especially in the Section 3.3.
Kernel functions are usually probability density functions, i.e. they integrate
to one and ![]() for all
for all ![]() in the domain of
in the domain of ![]() . An immediate
consequence of
. An immediate
consequence of
![]() is
is
![]() ,
i.e. the kernel density estimator is a pdf, too.
Moreover,
,
i.e. the kernel density estimator is a pdf, too.
Moreover,
![]() will inherit all the continuity and
differentiability properties of
will inherit all the continuity and
differentiability properties of ![]() . For instance, if
. For instance, if ![]() is
is ![]() times continuously differentiable then the same will hold true for
times continuously differentiable then the same will hold true for
![]() . On a more intuitive level this ``inheritance property'' of
. On a more intuitive level this ``inheritance property'' of
![]() is reflected in the smoothness of its graph.
Consider Figure 3.3 where,
for the same data set (stock returns) and a given value
of
is reflected in the smoothness of its graph.
Consider Figure 3.3 where,
for the same data set (stock returns) and a given value
of ![]() , kernel density estimates
have been graphed using different kernel functions.
, kernel density estimates
have been graphed using different kernel functions.
Note how the estimate based on the Uniform kernel (right) reflects the box shape of the underlying kernel function with its ragged behavior. The estimate that employed the smooth Quartic kernel function (left), on the other hand, gives a smooth and continuous picture.
Differences are not confined to estimates that are based on kernel
functions that are continuous or non-continuous. Even among estimates
based on continuous kernel functions there are considerable
differences in smoothness (for the same value of ![]() ) as you can
confirm by looking at Figure 3.4. Here, for
) as you can
confirm by looking at Figure 3.4. Here, for ![]() density estimates are graphed for income data from the Family
Expenditure Survey, using the Epanechnikov kernel (left) and
the Triweight kernel (right),
respectively. There is quite a difference in the smoothness of
the graphs of the two estimates.
density estimates are graphed for income data from the Family
Expenditure Survey, using the Epanechnikov kernel (left) and
the Triweight kernel (right),
respectively. There is quite a difference in the smoothness of
the graphs of the two estimates.
You might wonder how we will ever solve this dilemma: on one
hand we will be trying to find an optimal bandwidth ![]() but obviously a given
value of
but obviously a given
value of ![]() does not guarantee the same degree of smoothness if used
with different kernel functions. We will come back to this
problem in Section 3.4.2.
does not guarantee the same degree of smoothness if used
with different kernel functions. We will come back to this
problem in Section 3.4.2.
Before we turn to the statistical properties of kernel density estimators let us present another view on kernel density estimation that provides both further motivation as well as insight into how the procedure works. Look at Figure 3.5 where the kernel density estimate for an artificial data set is shown along with individual rescaled kernel functions.
What do we mean by a rescaled kernel function? The rescaled kernel function is simply