To discuss the choice of the kernel we will consider
equivalent kernels, i.e. kernel functions that lead to exactly the
same kernel density estimator. Consider a kernel function
![]() and
the following modification:
and
the following modification:
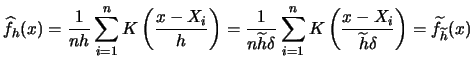
Different values of ![]() correspond to different members of an
equivalence class of kernels. We will now show how
Marron & Nolan (1988)
use the equivalence class idea to uncouple the problems of choosing
correspond to different members of an
equivalence class of kernels. We will now show how
Marron & Nolan (1988)
use the equivalence class idea to uncouple the problems of choosing ![]() and
and
![]() . Recall the
. Recall the ![]() criterion, i.e.
criterion, i.e.
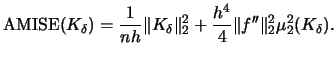 |
(3.43) |
What happens to ![]() if we use the very member
that corresponds to
if we use the very member
that corresponds to
![]() , namely the kernel
, namely the kernel
![]() ? By
construction, for
? By
construction, for
![]() we have
we have
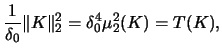
Because of these unique properties Marron and Nolan call
![]() the canonical kernel of an equivalence class.
Table 3.2 gives the canonical bandwidths
the canonical kernel of an equivalence class.
Table 3.2 gives the canonical bandwidths
![]() for selected (equivalence
classes of) kernels.
for selected (equivalence
classes of) kernels.
| Kernel |
|
||
| Uniform |
|
1.3510 | |
| Epanechnikov | 1.7188 | ||
| Quartic | 2.0362 | ||
| Triweight |
|
2.3122 | |
| Gaussian |
|
0.7764 |
In Subsection 3.1.4 we saw that the smoothness of two kernel density estimates with the same bandwidth but different kernel functions may be quite different. To get estimates based on two different kernel functions that have about the same degree of smoothness, we have to adjust one of the bandwidths by multiplying with an adjustment factor.
These adjustment factors can be easily computed from the canonical
bandwidths.
Suppose now that we have estimated an unknown density ![]() using some kernel
using some kernel
![]() and bandwidth
and bandwidth ![]() (
(![]() might stand for Epanechnikov,
for instance). We consider estimating
might stand for Epanechnikov,
for instance). We consider estimating ![]() with a different
kernel,
with a different
kernel, ![]() (
(![]() might stand for Gaussian,
say). Now we ask ourselves: what
bandwidth
might stand for Gaussian,
say). Now we ask ourselves: what
bandwidth ![]() should we use in the estimation with kernel
should we use in the estimation with kernel ![]() when we want to get approximately the same degree of smoothness as
we had in the case of
when we want to get approximately the same degree of smoothness as
we had in the case of ![]() and
and ![]() ?
The answer is given by the following formula:
?
The answer is given by the following formula:
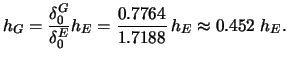
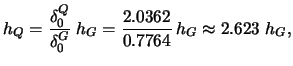
The scaling factors
![]() are also useful for finding an
optimal kernel function (see Exercise 3.6).
We turn your attention to this problem in the next section.
are also useful for finding an
optimal kernel function (see Exercise 3.6).
We turn your attention to this problem in the next section.
Recall that if we use canonical kernels the ![]() depends on
depends on ![]() only through a multiplicative constant
only through a multiplicative constant ![]() and we have effectively
separated the choice of
and we have effectively
separated the choice of ![]() from the choice of
from the choice of ![]() .
.
A question of immediate interest is to find the kernel that minimizes
![]() (this, of course, will be the kernel that minimizes
(this, of course, will be the kernel that minimizes ![]() with respect to
with respect to ![]() ). Epanechnikov (1969, the person, not the kernel) has
shown that under all nonnegative kernels with compact support, the
kernel of the form
). Epanechnikov (1969, the person, not the kernel) has
shown that under all nonnegative kernels with compact support, the
kernel of the form
Does this mean that one
should always use the Epanechnikov kernel? Before we can answer this
question we should compare the values of ![]() of other kernels with
the value of
of other kernels with
the value of ![]() for the Epanechnikov kernel. Table 3.3
shows that using, say, the Quartic kernel will lead to an
increase in
for the Epanechnikov kernel. Table 3.3
shows that using, say, the Quartic kernel will lead to an
increase in ![]() of less than half a percent.
of less than half a percent.
| Kernel |
|
|
| Uniform | 0.3701 | 1.0602 |
| Triangle | 0.3531 | 1.0114 |
| Epanechnikov | 0.3491 | 1.0000 |
| Quartic | 0.3507 | 1.0049 |
| Triweight | 0.3699 | 1.0595 |
| Gaussian | 0.3633 | 1.0408 |
| Cosine | 0.3494 | 1.0004 |
After all, we can conclude that for practical purposes the choice of the kernel function is almost irrelevant for the efficiency of the estimate.