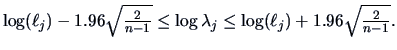In practice, PCs are computed from sample data.
The following theorem yields results on the asymptotic distribution
of the sample PCs.
EXAMPLE 9.4
Since
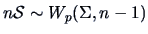
if
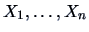
are drawn from
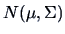
, we have that
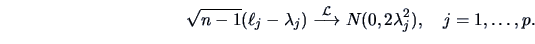 |
(9.17) |
Since the variance of (
9.17) depends on the true mean
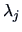
a log transformation is useful. Consider
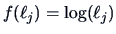
. Then
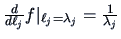
and by the
Transformation Theorem
4.11 we have from (
9.17) that
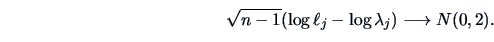 |
(9.18) |
Hence,
and a two-sided confidence interval at the
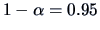
significance level is given by
In the bank data example we have that
Therefore,
It can be concluded for the true eigenvalue that
The variance explained by the first 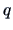 PCs
is given by
PCs
is given by
In practice this is estimated by
From Theorem 9.4 we know the distribution of
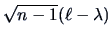 .
Since
.
Since 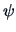 is a nonlinear function of
is a nonlinear function of 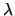 , we can again
apply the Transformation Theorem 4.11 to obtain that
, we can again
apply the Transformation Theorem 4.11 to obtain that
where
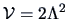 (from Theorem 9.4) and
(from Theorem 9.4) and
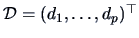 with
with
Given this result, the following theorem can be derived.
EXAMPLE 9.5
From Section
9.3 it is known that the first PC for the Swiss
bank notes resolves 67% of the variation. It can be tested whether
the true proportion is actually 75%. Computing
Hence, a confidence interval at a significance of level
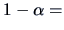
0.95 is given by
Clearly the hypothesis that
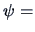
75% can be rejected!
Summary

-
The eigenvalues
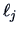 and eigenvectors
and eigenvectors 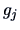 are
asymptotically, normally distributed, in particular
are
asymptotically, normally distributed, in particular
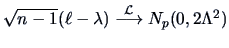 .
.

-
For the eigenvalues it holds that
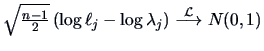 .
.

-
Given an asymptotic, normal distribution approximate confidence
intervals and tests can be constructed
for the proportion of variance which is explained by the first
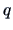 PCs.
The two-sided confidence interval at the
PCs.
The two-sided confidence interval at the
 level is given by
level is given by
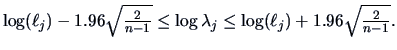

-
It holds for
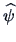 , the estimate of
, the estimate of 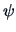 (the proportion
of the variance explained by the first
(the proportion
of the variance explained by the first 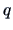 PCs) that
PCs) that
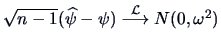 , where
, where 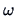 is given in Theorem 9.5.
is given in Theorem 9.5.
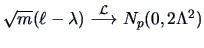 ,
,
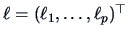 and
and
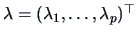 are the diagonals of
are the diagonals of
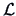 and
and 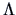 ,
,
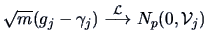 ,
,
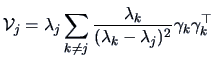 ,
,
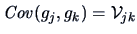 ,
,
 -element of the matrix
-element of the matrix
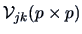 is
is
![$\displaystyle -\frac{\lambda _j\lambda _k\gamma _{rk}\gamma _{sj} }
{[m(\lambda _j-\lambda _k)^2] }$](mvahtmlimg2755.gif) ,
,
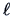 are asymptotically independent of the elements
in
are asymptotically independent of the elements
in 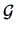 .
.
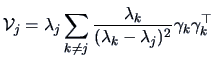 ,
,
![$\displaystyle -\frac{\lambda _j\lambda _k\gamma _{rk}\gamma _{sj} }
{[m(\lambda _j-\lambda _k)^2] }$](mvahtmlimg2755.gif) ,
,
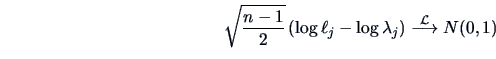
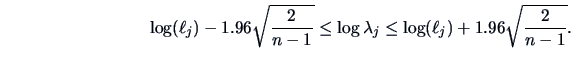
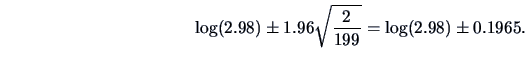
![]() PCs
is given by
PCs
is given by


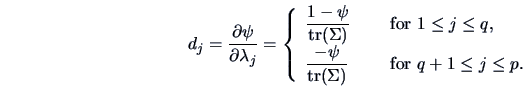
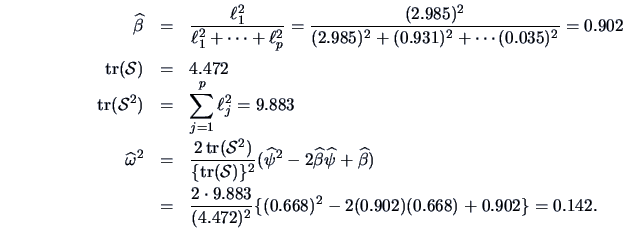
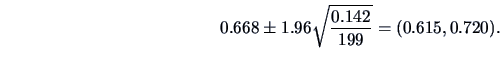
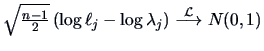 .
.