11.3 Cluster Algorithms
There are essentially two types of clustering methods: hierarchical
algorithms and partioning algorithms. The hierarchical algorithms can
be divided into agglomerative and splitting procedures. The
first type of hierarchical clustering starts from the finest
partition possible (each observation forms a cluster) and groups them.
The second type starts with the coarsest
partition possible: one cluster contains all of the observations.
It proceeds by splitting the single cluster up into smaller
sized clusters.
The partioning algorithms start from a given group definition and
proceed by exchanging elements between groups until a certain score
is optimized. The main difference between the two clustering
techniques is that in hierarchical clustering once groups are found
and elements are assigned to
the groups, this assignment cannot be
changed. In partitioning techniques, on the other hand,
the assignment of objects into
groups may change during the algorithm application.
Hierarchical Algorithms, Agglomerative Techniques
Agglomerative algorithms are used quite frequently in practice. The
algorithm consists of the following steps:
If two objects or groups say, 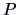 and
and 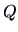 , are united, one computes the
distance between this new group (object)
, are united, one computes the
distance between this new group (object) 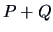 and group
and group 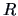 using
the following distance function:
using
the following distance function:
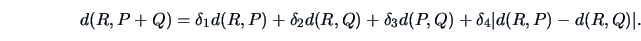 |
(11.9) |
The 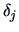 's are weighting factors that lead to different
agglomerative algorithms as described in Table 11.2.
Here
's are weighting factors that lead to different
agglomerative algorithms as described in Table 11.2.
Here
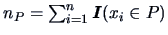 is the number of
objects in group
is the number of
objects in group 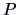 . The values of
. The values of 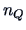 and
and 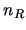 are defined
analogously.
are defined
analogously.
Table 11.2:
Computations of group distances.
| Name |
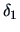 |
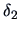 |
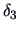 |
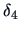 |
| Single linkage |
1/2 |
1/2 |
0 |
-1/2 |
| Complete linkage |
1/2 |
1/2 |
0 |
1/2 |
Average linkage
(unweighted) |
1/2 |
1/2 |
0 |
0 |
Average linkage
(weighted) |
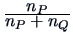 |
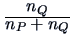 |
0 |
0 |
| Centroid |
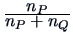 |
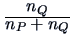 |
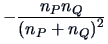 |
0 |
| Median |
1/2 |
1/2 |
-1/4 |
0 |
| Ward |
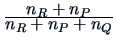 |
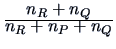 |
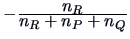 |
0 |
|
EXAMPLE 11.4
Let us examine the agglomerative algorithm
for the three points in Example
11.2,
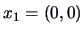
,
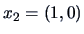
and
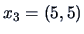
, and the squared Euclidean distance matrix
with single linkage weighting. The algorithm starts with
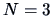
clusters:
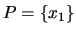
,
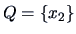
and
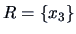
.
The distance matrix
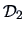
is given in Example
11.2. The smallest distance in
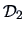
is
the one between the clusters
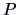
and
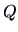
. Therefore, applying step 4 in
the above algorithm we combine these clusters to form
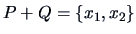
. The single linkage distance between the remaining two
clusters is from Table
11.2 and (
11.9) equal to
The reduced distance matrix is then
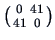
. The next and last step is to unite
the clusters
and
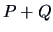
into a single cluster

, the original
data matrix.
When there are more data points than in the example above,
a visualization of the
implication of clusters is desirable. A graphical representation of
the sequence of clustering is called a dendrogram.
It displays
the observations, the sequence of clusters and the distances between
the clusters. The vertical axis displays the indices of the points, whereas
the horizontal axis gives the distance between the clusters.
Large distances indicate the clustering of heterogeneous
groups. Thus, if we choose to ``cut the tree'' at a desired level, the
branches describe the corresponding clusters.
EXAMPLE 11.5
Here we describe the single linkage algorithm for the
eight data points displayed in Figure
11.1.
The distance matrix (
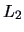
-norms) is
and the dendrogram is shown in Figure
11.2.
Figure 11.2:
The dendrogram for the 8-point example, Single
linkage algorithm.
 MVAclus8p.xpl
MVAclus8p.xpl
|
|
If we decide to cut the tree at the level 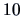 , three
clusters are defined:
, three
clusters are defined: 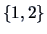 ,
, 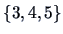 and
and 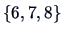 .
.
The single linkage algorithm defines
the distance between two
groups as the smallest value of the individual distances.
Table 11.2 shows that in this case
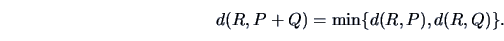 |
(11.11) |
This algorithm is also called the
Nearest Neighbor algorithm.
As a consequence of its construction,
single linkage tends to build large groups.
Groups that differ but are not well separated may thus be
classified into one group as long as they have two approximate points.
The complete linkage algorithm tries to correct
this kind of grouping by
considering the largest (individual) distances. Indeed,
the complete linkage distance can be written as
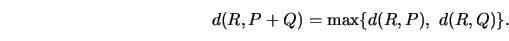 |
(11.12) |
It is also called the
Farthest Neighbor algorithm.
This algorithm will cluster groups where all the points are proximate,
since it compares the largest distances.
The average linkage algorithm (weighted or unweighted) proposes
a compromise between the two preceding algorithms,
in that it computes an average distance:
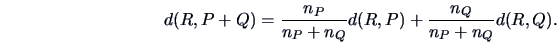 |
(11.13) |
The centroid algorithm is quite similar
to the average linkage algorithm and uses
the natural geometrical distance between 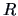 and the weighted center of
gravity of
and the weighted center of
gravity of 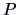 and
and 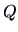 (see Figure 11.3):
(see Figure 11.3):
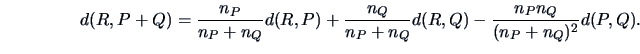 |
(11.14) |
Figure 11.3:
The centroid algorithm.
![\begin{figure}\begin{center}
\begin{picture}(110.00,54.00)
% emline\{28.00\}\{22...
...c]{weighted center of gravity of $P+Q$}}
\end{picture} \end{center} \end{figure}](mvahtmlimg3302.gif) |
The Ward clustering algorithm computes the distance between groups
according to the formula in Table 11.2. The main difference
between this algorithm and the linkage procedures is in the
unification procedure. The Ward algorithm does not put together groups
with smallest distance. Instead, it joins groups that do not increase
a given measure of heterogeneity ``too much''.
The aim of the Ward procedure is to
unify groups such that the variation inside these groups does not
increase too drastically: the resulting groups are as homogeneous as
possible.
The heterogeneity of group 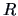 is measured by the inertia inside the
group. This inertia is defined as follows:
is measured by the inertia inside the
group. This inertia is defined as follows:
 |
(11.15) |
where
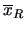 is the center of gravity (mean) over the
groups.
is the center of gravity (mean) over the
groups. 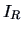 clearly provides a scalar measure of the dispersion
of the group around its center of gravity. If the usual Euclidean
distance is used, then
clearly provides a scalar measure of the dispersion
of the group around its center of gravity. If the usual Euclidean
distance is used, then 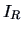 represents the sum of the variances of the
represents the sum of the variances of the  components of
components of 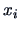 inside group
inside group 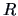 .
.
When two objects or groups 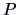 and
and 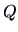 are joined, the new group
are joined, the new group
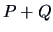 has a larger inertia
has a larger inertia 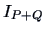 . It can be shown that the
corresponding increase of inertia is given by
. It can be shown that the
corresponding increase of inertia is given by
 |
(11.16) |
In this case,
the Ward algorithm is defined as an algorithm that
``joins the groups that give
the smallest increase in 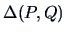 ''. It is easy to prove that
when
''. It is easy to prove that
when 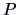 and
and 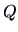 are joined, the new criterion values are
given by (11.9) along with the values of
are joined, the new criterion values are
given by (11.9) along with the values of 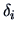 given
in Table 11.2, when the centroid formula is used to modify
given
in Table 11.2, when the centroid formula is used to modify
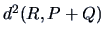 .
So, the Ward algorithm is related to the centroid algorithm, but
with an ``inertial'' distance
.
So, the Ward algorithm is related to the centroid algorithm, but
with an ``inertial'' distance  rather than the ``geometric''
distance
rather than the ``geometric''
distance 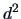 .
.
As pointed out in Section 11.2, all the algorithms above can
be adjusted by the choice of the metric 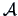 defining the
geometric distance
defining the
geometric distance 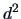 . If the results of a clustering algorithm
are illustrated as graphical representations of individuals in spaces
of low dimension (using principal components (normalized or not) or
using a correspondence analysis for contingency tables), it is important to
be coherent in the choice of the metric used.
. If the results of a clustering algorithm
are illustrated as graphical representations of individuals in spaces
of low dimension (using principal components (normalized or not) or
using a correspondence analysis for contingency tables), it is important to
be coherent in the choice of the metric used.
EXAMPLE 11.6
As an example we randomly select 20
observations from the bank notes data and apply the Ward technique using
Euclidean distances.
Figure
11.4 shows the first two PCs of these data,
Figure
11.5 displays the dendrogram.
Figure 11.5:
The dendrogram for the 20 bank notes, Ward algorithm.
 MVAclusbank.xpl
MVAclusbank.xpl
|
|
EXAMPLE 11.7
Consider the French food expenditures. As in Chapter
9
we use standardized data which is equivalent to using
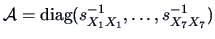
as the weight matrix in the
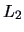
-norm. The NPCA plot of the
individuals was given in Figure
9.7.
The Euclidean distance matrix is of course given by (
11.6).
The dendrogram obtained by using the Ward algorithm is shown in
Figure
11.6.
Figure 11.6:
The dendrogram for the French food expenditures,
Ward algorithm.
 MVAclusfood.xpl
MVAclusfood.xpl
|
|
If the aim was to have only two groups, as can be seen in
Figure 11.6 , they would be
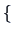 CA2, CA3, CA4, CA5, EM5
CA2, CA3, CA4, CA5, EM5 and
and
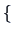 MA2, MA3, MA4, MA5, EM2, EM3, EM4
MA2, MA3, MA4, MA5, EM2, EM3, EM4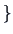 .
Clustering three groups is somewhat arbitrary (the levels of the
distances are too similar). If we were
interested in four groups, we would obtain
.
Clustering three groups is somewhat arbitrary (the levels of the
distances are too similar). If we were
interested in four groups, we would obtain
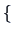 CA2, CA3, CA4
CA2, CA3, CA4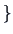 ,
,
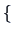 EM2, MA2, EM3, MA3
EM2, MA2, EM3, MA3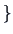 ,
,
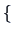 EM4, MA4, MA5
EM4, MA4, MA5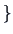 and
and
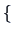 EM5, CA5
EM5, CA5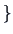 .
This grouping shows a balance between socio-professional levels and size of
the families in determining the clusters. The four groups are clearly
well represented in the NPCA plot in Figure 9.7.
.
This grouping shows a balance between socio-professional levels and size of
the families in determining the clusters. The four groups are clearly
well represented in the NPCA plot in Figure 9.7.
Summary

-
The class of clustering algorithms can be divided into two types:
hierarchical and partitioning algorithms.
Hierarchical algorithms start with the finest (coarsest) possible
partition and put groups together (split groups apart) step by step.
Partitioning algorithms start from a preliminary clustering and
exchange group elements until a certain score is reached.

-
Hierarchical agglomerative techniques are frequently used in practice.
They start
from the finest possible structure (each data point forms a cluster),
compute the distance matrix for the clusters and join the clusters
that have the smallest distance. This step is repeated until all points are
united in one cluster.

-
The agglomerative procedure depends on the definition of the distance
between two clusters. Single linkage,
complete linkage, and Ward distance are frequently used distances.

-
The process of the unification of
clusters can be graphically represented by a dendrogram.
![]() and
and ![]() , are united, one computes the
distance between this new group (object)
, are united, one computes the
distance between this new group (object) ![]() and group
and group ![]() using
the following distance function:
using
the following distance function:
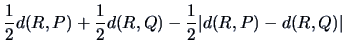
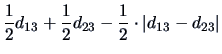
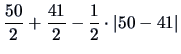
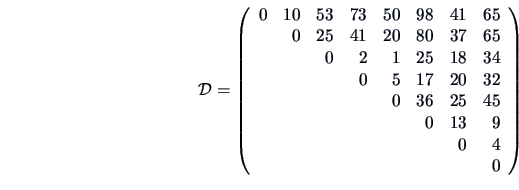
![]() , three
clusters are defined:
, three
clusters are defined: ![]() ,
, ![]() and
and ![]() .
.
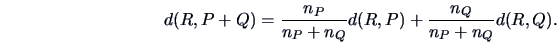
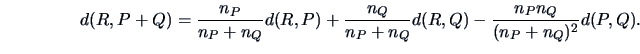
![]() is measured by the inertia inside the
group. This inertia is defined as follows:
is measured by the inertia inside the
group. This inertia is defined as follows:

![]() and
and ![]() are joined, the new group
are joined, the new group
![]() has a larger inertia
has a larger inertia ![]() . It can be shown that the
corresponding increase of inertia is given by
. It can be shown that the
corresponding increase of inertia is given by
![]() defining the
geometric distance
defining the
geometric distance ![]() . If the results of a clustering algorithm
are illustrated as graphical representations of individuals in spaces
of low dimension (using principal components (normalized or not) or
using a correspondence analysis for contingency tables), it is important to
be coherent in the choice of the metric used.
. If the results of a clustering algorithm
are illustrated as graphical representations of individuals in spaces
of low dimension (using principal components (normalized or not) or
using a correspondence analysis for contingency tables), it is important to
be coherent in the choice of the metric used.
![]() CA2, CA3, CA4, CA5, EM5
CA2, CA3, CA4, CA5, EM5![]() and
and
![]() MA2, MA3, MA4, MA5, EM2, EM3, EM4
MA2, MA3, MA4, MA5, EM2, EM3, EM4![]() .
Clustering three groups is somewhat arbitrary (the levels of the
distances are too similar). If we were
interested in four groups, we would obtain
.
Clustering three groups is somewhat arbitrary (the levels of the
distances are too similar). If we were
interested in four groups, we would obtain
![]() CA2, CA3, CA4
CA2, CA3, CA4![]() ,
,
![]() EM2, MA2, EM3, MA3
EM2, MA2, EM3, MA3![]() ,
,
![]() EM4, MA4, MA5
EM4, MA4, MA5![]() and
and
![]() EM5, CA5
EM5, CA5![]() .
This grouping shows a balance between socio-professional levels and size of
the families in determining the clusters. The four groups are clearly
well represented in the NPCA plot in Figure 9.7.
.
This grouping shows a balance between socio-professional levels and size of
the families in determining the clusters. The four groups are clearly
well represented in the NPCA plot in Figure 9.7.